So berechnen sie normalwahrscheinlichkeiten mit einem ti-84-rechner

Die Normalverteilung ist die in allen Statistiken am häufigsten verwendete Verteilung. In diesem Tutorial wird erklärt, wie Sie die folgenden Funktionen auf einem TI-84-Rechner verwenden, um Normalverteilungswahrscheinlichkeiten zu ermitteln:

normalpdf(x, μ, σ) gibt die mit dem normalen PDF verbundene Wahrscheinlichkeit zurück, wobei:

• x = Einzelwert
• μ = Bevölkerungsmittelwert
• σ = Populationsstandardabweichung

normalcdf(lower_x, Upper_x, μ, σ) gibt die kumulative Wahrscheinlichkeit zurück, die mit der normalen cdf zwischen zwei Werten verbunden ist.

Gold:

• Lower_x = unterer Einzelwert
• Upper_x = oberer Einzelwert
• μ = Bevölkerungsmittelwert
• σ = Populationsstandardabweichung

Auf diese beiden Funktionen können Sie auf einem TI-84-Rechner zugreifen, indem Sie 2nd und dann vars drücken. Dadurch gelangen Sie zu einem DISTR- Bildschirm, in dem Sie dann normalpdf() und normalcdf() verwenden können:

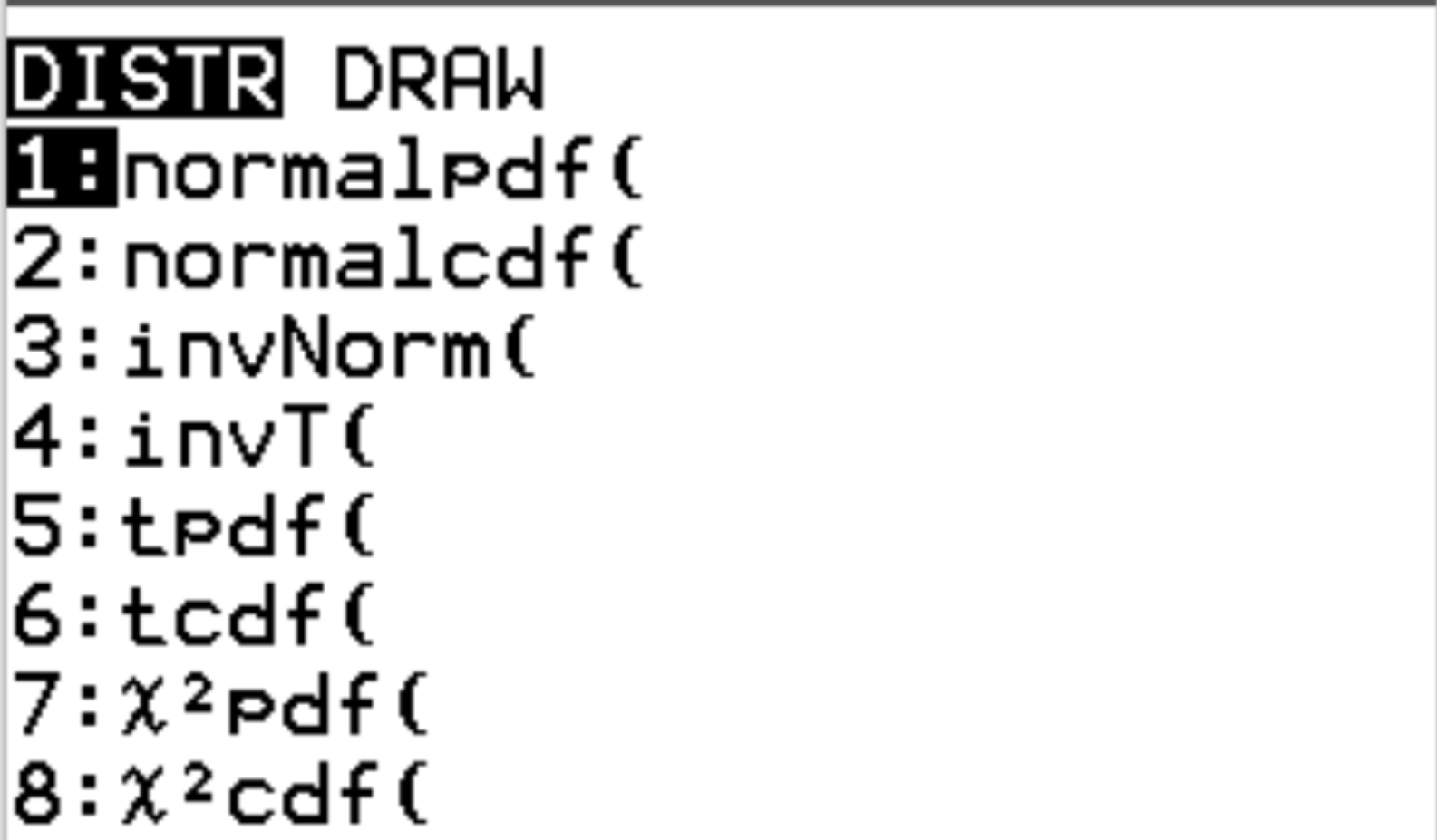
Die folgenden Beispiele veranschaulichen, wie Sie diese Funktionen zur Beantwortung verschiedener Fragen verwenden.

Beispiel 1: Normalwahrscheinlichkeit größer als x

Frage: Ermitteln Sie für eine Normalverteilung mit Mittelwert = 40 und Standardabweichung = 6 die Wahrscheinlichkeit, dass ein Wert größer als 45 ist.

Antwort: Verwenden Sie die Funktion normalcdf(x, 10000, μ, σ):

normalcdf(45, 10000, 40, 6) = 0,2023

Hinweis: Da die Funktion einen oberen_x-Wert erfordert, verwenden wir einfach 10.000.

Beispiel 2: Normalwahrscheinlichkeit kleiner als x

Frage: Ermitteln Sie für eine Normalverteilung mit Mittelwert = 100 und Standardabweichung = 11,3 die Wahrscheinlichkeit, dass ein Wert kleiner als 98 ist.

Antwort: Verwenden Sie die Funktion normalcdf(-10000, x, μ, σ):

normalcdf(-10000, 98, 100, 11,3) = 0,4298

Hinweis: Da die Funktion einen niedrigeren_x-Wert erfordert, verwenden wir einfach -10000.

Beispiel 3: Normalwahrscheinlichkeit zwischen zwei Werten

Frage: Ermitteln Sie für eine Normalverteilung mit Mittelwert = 50 und Standardabweichung = 4 die Wahrscheinlichkeit, dass ein Wert zwischen 48 und 52 liegt.

Antwort: Verwenden Sie die Funktion normalcdf(smaller_x, Larger_x, μ, σ).

normalcdf(48, 52, 50, 4) = 0,3829

Beispiel 4: Normalwahrscheinlichkeit außer zwei Werten

Frage: Ermitteln Sie für eine Normalverteilung mit Mittelwert = 22 und Standardabweichung = 4 die Wahrscheinlichkeit, dass ein Wert kleiner als 20 oder größer als 24 ist.

Antwort: Verwenden Sie die Funktion normalcdf(-10000, small_x, μ, σ) + normalcdf(larger_x, 10000, μ, σ)

normalcdf(-10000, 20, 22, 4) + normalcdf(24, 10000, 22, 4) = 0,6171