Np-steuerkarte

Von Dr. Benjamin Anderson August 1, 2023 Qualitätsmanagement Keine Kommentare

In diesem Artikel zeigen wir Ihnen, was eine NP-Kontrollkarte ist und wofür sie verwendet wird. Darüber hinaus können Sie eine gelöste Übung sehen, in der wir erklären, wie man eine NP-Kontrollkarte erstellt.

Was ist eine NP-Kontrollkarte?

Eine NP-Kontrollkarte oder einfach NP-Karte ist ein Diagramm, in dem die Anzahl fehlerhafter Einheiten aus mehreren Stichproben konstanter Größe aufgetragen wird.

Mithilfe einer NP-Kontrollkarte wird überwacht, dass die Anzahl fehlerhafter Einheiten in einem Prozess die Kontrollgrenzen nicht überschreitet.

Beispielsweise kann eine NP-Kontrollkarte verwendet werden, um die Entwicklung fehlerhafter Produkte zu analysieren, die durch einen Produktionsprozess erzeugt werden. Auf diese Weise können wir erkennen, dass ein Problem im Produktionsprozess vorliegt, wenn die Anzahl fehlerhafter Produkte die Kontrollgrenzen überschreitet.

Es ist wichtig zu beachten, dass die NP-Kontrollkarte im Gegensatz zu einer P-Kontrollkarte nicht den Anteil defekter Einheiten, sondern die Anzahl defekter Einheiten überwacht. Darüber hinaus muss die Größe aller Stichproben gleich sein.

So erstellen Sie eine NP-Kontrollkarte

Die Schritte zum Erstellen eines NP-Kontrolldiagramms lauten wie folgt:

Nehmen Sie Proben : Zunächst müssen Sie verschiedene Proben entnehmen, um die Entwicklung der Anzahl defekter Einheiten in der Grafik zu sehen. Die Proben müssen gleich groß sein. Darüber hinaus wird empfohlen, mindestens 20 Proben zu entnehmen und die Probengröße größer als 50 zu sein.
Zählen Sie die Anzahl der defekten Einheiten : Für jede Stichprobe muss die Anzahl der Einheiten mit mindestens einem Defekt ermittelt werden.
Berechnen Sie den Durchschnittswert des Anteils : Aus allen untersuchten Elementen müssen Sie den Gesamtanteil defekter Einheiten berechnen.

$\overline{p}=\cfrac{\text{N\'umero total de unidades defectuosas}}{\text{N\'umero total de unidades}}$

Berechnen Sie die Kontrollgrenzen anhand der NP-Karte : Für jede getestete Probe müssen Sie ihre Kontrollgrenzen mithilfe der folgenden Formeln ermitteln:

$\displaystyle LCS=n\overline{p}+3\sqrt{n\overline{p}(1-\overline{p})}$

$\displaystyle LCI=n\overline{p}-3\sqrt{n\overline{p}(1-\overline{p})}$

Gold

$LCS$

Und

$LCI$

sind die oberen bzw. unteren Kontrollgrenzen,

$\overline{p}$

ist der Durchschnittswert des Fehleranteils und

$n$

ist die Stichprobengröße.

Tragen Sie die Werte in der Grafik ein : Jetzt müssen Sie die Werte der Anzahl der erhaltenen Fehler zusammen mit den im vorherigen Schritt berechneten Kontrollgrenzen in einer Grafik darstellen.
Analysieren Sie das NP-Kontrolldiagramm : Abschließend muss nur noch überprüft werden, ob kein Wert außerhalb der Kontrollgrenzen des Diagramms liegt und der Prozess somit unter Kontrolle ist. Andernfalls müssen Maßnahmen zur Korrektur des Produktionsprozesses ergriffen werden.

Beispiel einer NP-Kontrollkarte

Als nächstes werden wir anhand eines Schritt-für-Schritt-Lösungsbeispiels sehen, wie man ein NP-Kontrolldiagramm erstellt.

Ein Industrieunternehmen hat Proben von 100 Einheiten gesammelt und die Anzahl der fehlerhaften Teile in jeder Probe analysiert. Die aufgezeichneten Werte können Sie der folgenden Tabelle entnehmen. Erstellen Sie mit den erhaltenen Daten ein NP-Kontrolldiagramm.

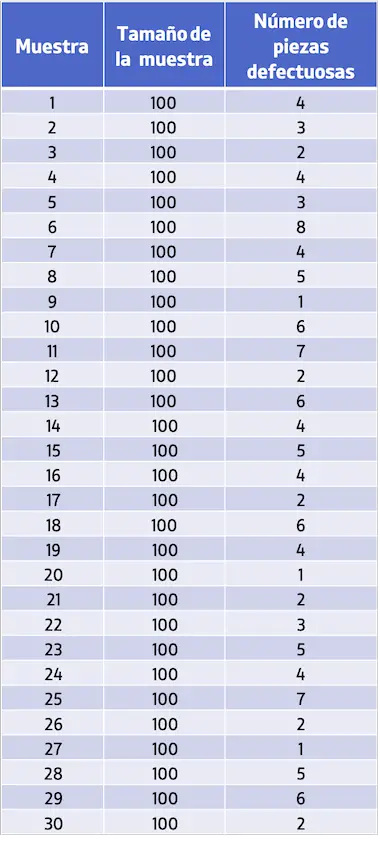
Wie Sie sehen, haben alle untersuchten Stichproben die gleiche Größe und darüber hinaus ist die Stichprobengröße größer als 50 Einheiten, sodass die Merkmale zur Erstellung einer NP-Kontrollkarte erfüllt sind.

Um das NP-Diagramm zu erstellen, müssen wir also zunächst die durchschnittliche Anzahl defekter Einheiten berechnen. Wenden Sie dazu einfach die folgende Formel an:

$\overline{p}=\cfrac{\text{N\'umero total de unidades defectuosas}}{\text{N\'umero total de unidades}}=\cfrac{118}{30\cdot 100}=0,039$

Wir berechnen nun die NP-Kartenkontrollgrenzen mit den Formeln, die wir oben gesehen haben:

$\begin{aligned}\displaystyle LCS&=n\overline{p}+3\sqrt{n\overline{p}(1-\overline{p})}\\[2ex]&=100\cdot 0,039+3\sqrt{100\cdot 0,039(1-0,039)}\\[2ex]&=9,76\end{aligned}$

$\begin{aligned}\displaystyle LCI&=n\overline{p}-3\sqrt{n\overline{p}(1-\overline{p})}\\[2ex]&=100\cdot 0,039-3\sqrt{100\cdot 0,039(1-0,039)}\\[2ex]&=-1,9\end{aligned}$

Die untere Kontrollgrenze ist negativ geworden, was keinen Sinn ergibt, da fehlerhafte negative Einheiten nicht hergestellt werden können. Daher setzen wir die untere Eingriffsgrenze auf 0.

Nachdem wir die Kontrollgrenzen berechnet haben, tragen wir alle Werte in die NP-Kontrollkarte ein:

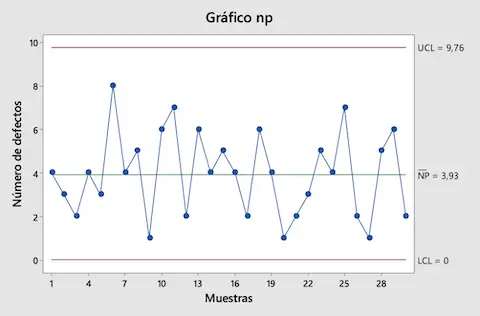
Wie Sie dem NP-Diagramm entnehmen können, liegen alle aus den Proben erfassten Werte zwischen den Kontrollgrenzen, sodass der Schluss gezogen werden kann, dass der Produktionsprozess unter Kontrolle ist.

Andere Arten von Kontrollkarten

Neben der NP-Regelkarte gibt es im Qualitätsmanagement noch weitere Arten von Attributregelkarten:

P-Kontrollkarte : Der Anteil fehlerhafter Produkte wird kontrolliert.
Steuerkarte C : Die Anzahl der auftretenden Fehler wird überwacht.
Kontrollkarte U : Die Anzahl der Fehler wird wie in Karte C kontrolliert, die Stichprobengröße ist jedoch variabel.

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen