Die nullhypothese für anova-modelle verstehen

Eine einfaktorielle ANOVA wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen besteht.

Eine einfaktorielle ANOVA verwendet die folgenden Null- und Alternativhypothesen:

• H ₀ : μ ₁ = μ ₂ = μ ₃ = … = μ _k (alle Gruppenmittelwerte sind gleich)
• H _A : Mindestens ein Gruppendurchschnitt ist unterschiedlich   ausruhen

Um zu entscheiden, ob wir die Nullhypothese ablehnen sollten oder nicht, müssen wir uns auf den p-Wert im Ergebnis der ANOVA-Tabelle beziehen.

Wenn der p-Wert unter einem bestimmten Signifikanzniveau liegt (z. B. 0,05), können wir die Nullhypothese ablehnen und daraus schließen, dass nicht alle Gruppenmittelwerte gleich sind.

Eine zweifaktorielle ANOVA wird verwendet, um zu bestimmen, ob ein statistisch signifikanter Unterschied zwischen den Mittelwerten von drei oder mehr unabhängigen Gruppen besteht, die zwei Variablen (manchmal auch „Faktoren“ genannt) zugeordnet wurden.

Eine zweifaktorielle ANOVA testet drei Nullhypothesen gleichzeitig:

• Alle Gruppenmittelwerte sind auf jeder Ebene der ersten Variablen gleich
• Alle Gruppenmittelwerte sind auf jeder Ebene der zweiten Variablen gleich
• Es gibt keinen Interaktionseffekt zwischen den beiden Variablen

Um zu entscheiden, ob wir jede Nullhypothese ablehnen sollten oder nicht, müssen wir uns auf die p-Werte im Ergebnis der zweifaktoriellen ANOVA-Tabelle beziehen.

Die folgenden Beispiele zeigen, wie Sie entscheiden, ob die Nullhypothese in einer einfaktoriellen ANOVA und einer zweifaktoriellen ANOVA abgelehnt werden soll oder nicht.

Beispiel 1: Einfaktorielle ANOVA

Angenommen, wir möchten wissen, ob drei verschiedene Prüfungsvorbereitungsprogramme zu unterschiedlichen Durchschnittsergebnissen bei einer bestimmten Prüfung führen. Um dies zu testen, rekrutieren wir 30 Studierende für die Teilnahme an einer Studie und teilen sie in drei Gruppen auf.

Den Schülern jeder Gruppe wird nach dem Zufallsprinzip zugeteilt , dass sie in den folgenden drei Wochen eines von drei Prüfungsvorbereitungsprogrammen nutzen sollen, um sich auf eine Prüfung vorzubereiten. Am Ende der drei Wochen legen alle Studierenden die gleiche Prüfung ab.

Die Prüfungsergebnisse für jede Gruppe sind unten aufgeführt:

Wenn wir diese Werte in den einfaktoriellen ANOVA-Rechner eingeben, erhalten wir als Ausgabe die folgende ANOVA-Tabelle:

Beachten Sie, dass der p-Wert 0,11385 beträgt.

Für dieses spezielle Beispiel würden wir die folgenden Null- und Alternativhypothesen verwenden:

• H ₀ : μ ₁ = μ ₂ = μ ₃ (die durchschnittliche Prüfungspunktzahl für jede Gruppe ist gleich)
• H _A : Mindestens ein Gruppendurchschnitt ist unterschiedlich   ausruhen

Da der p-Wert der ANOVA-Tabelle nicht kleiner als 0,05 ist, können wir die Nullhypothese nicht ablehnen.

Das bedeutet, dass uns keine ausreichenden Beweise dafür vorliegen, dass es einen statistisch signifikanten Unterschied zwischen den durchschnittlichen Prüfungsergebnissen der drei Gruppen gibt.

Beispiel 2: Zweifaktorielle ANOVA

Angenommen, ein Botaniker möchte wissen, ob das Pflanzenwachstum durch die Sonneneinstrahlung und die Häufigkeit des Gießens beeinflusst wird.

Sie pflanzt 40 Samen und lässt sie zwei Monate lang unter unterschiedlichen Bedingungen der Sonneneinstrahlung und Bewässerungshäufigkeit wachsen. Nach zwei Monaten zeichnet sie die Höhe jeder Pflanze auf. Die Ergebnisse sind unten dargestellt:

In der Tabelle oben sehen wir, dass in jeder Kombination von Bedingungen fünf Pflanzen gezüchtet wurden.

Beispielsweise wurden fünf Pflanzen mit täglicher Bewässerung und ohne Sonnenlicht gezüchtet und ihre Höhen betrugen nach zwei Monaten 4,8 Zoll, 4,4 Zoll, 3,2 Zoll, 3,9 Zoll und 4,4 Zoll:

Sie führt eine zweifaktorielle ANOVA in Excel durch und erhält das folgende Ergebnis:

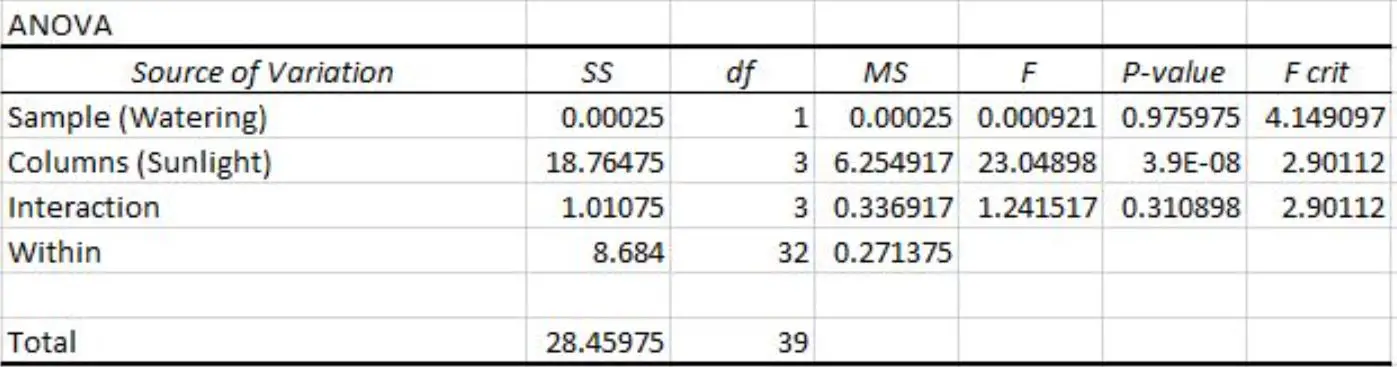
Wir können die folgenden p-Werte im Ergebnis der Zwei-Wege-ANOVA-Tabelle sehen:

• Der p-Wert für die Bewässerungshäufigkeit beträgt 0,975975 . Dies ist auf dem Signifikanzniveau von 0,05 statistisch nicht signifikant.
• Der p-Wert für Sonneneinstrahlung beträgt 3,9E-8 (0,000000039) . Dies ist bei einem Signifikanzniveau von 0,05 statistisch signifikant.
• Der p-Wert für die Wechselwirkung zwischen Bewässerungshäufigkeit und Sonneneinstrahlung beträgt 0,310898 . Dies ist auf dem Signifikanzniveau von 0,05 statistisch nicht signifikant.

Diese Ergebnisse deuten darauf hin, dass die Sonneneinstrahlung der einzige Faktor ist, der einen statistisch signifikanten Einfluss auf die Pflanzenhöhe hat.

Und da es keinen Wechselwirkungseffekt gibt, ist der Effekt der Sonneneinstrahlung bei jeder Bewässerungshäufigkeit gleichbleibend.

Einfach ausgedrückt: Ob eine Pflanze täglich oder wöchentlich gegossen wird, hat keinen Einfluss darauf, wie sich Sonneneinstrahlung auf eine Pflanze auswirkt.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu ANOVA-Modellen:

So interpretieren Sie den F-Wert und den P-Wert in der ANOVA
So berechnen Sie die Quadratsumme in der ANOVA
Was bedeutet ein hoher F-Wert in der ANOVA?