Obere und untere zäune: definition und beispiel

In der Statistik stellen Ober- und Untergrenzen Schwellenwerte für obere und untere Ausreißer in einem Datensatz dar. Sie werden wie folgt berechnet:

• Unterer Schlusskurs = Q1 – (1,5*IQR)
• Oberer Schlusskurs = Q3 + (1,5*IQR)

Dabei steht IQR für „Interquartilbereich“, der den Unterschied zwischen dem 75. Perzentil (Q3) und dem 25. Perzentil (Q1) in einem Datensatz darstellt.

Eine Beobachtung oberhalb der oberen Barriere oder unterhalb der unteren Barriere wird oft als Ausreißer betrachtet.

Beispiel: Berechnung des oberen und unteren Zauns

Angenommen, wir haben den folgenden Datensatz:

 Dataset: 11, 13, 14, 14, 15, 16, 18, 22, 24, 27, 34, 36, 38, 41, 45

Mit den folgenden Schritten können wir den oberen und unteren Zaun des Datensatzes berechnen:

Schritt 1: Suchen Sie nach Q1 und Q3.

Q1 stellt das 25. Perzentil des Datensatzes dar und Q3 stellt das 75. Perzentil dar. Laut dem Interquartilbereichsrechner sind Q1 und Q3 für diesen Datensatz:

• T1: 14
• T3: 36

Schritt 2: Finden Sie den IQR (Interquartilbereich).

Der Interquartilbereich stellt die Differenz zwischen Q3 und Q1 dar, die wie folgt berechnet wird:

• Interquartilskala: Q3 – Q1 = 36 – 14 = 22

Schritt 3: Finden Sie den oberen und unteren Zaun

Zur Berechnung der oberen und unteren Zäune können wir folgende Formeln verwenden:

• Unterer Schlusskurs: Q1 – (1,5*IQR) = 14 – (1,5*22) = -19
• Oberer Zaun: Q3 + (1,5*IQR) = 36 + (1,5*22) = 69

Da keine der Beobachtungen in unserem Datensatz unter den unteren oder über den oberen Zaun fällt, würde keine der Beobachtungen als Ausreißer betrachtet.

Wir können auch ein Boxplot erstellen, um unsere Verteilung der Datenwerte sowie die oberen und unteren Zäune zu visualisieren:

Bonus: Rechner für obere und untere Schlusskurse

Anstatt den oberen und unteren Zaun eines Datensatzes manuell zu berechnen, können Sie auch den Rechner für den oberen und unteren Zaun verwenden:

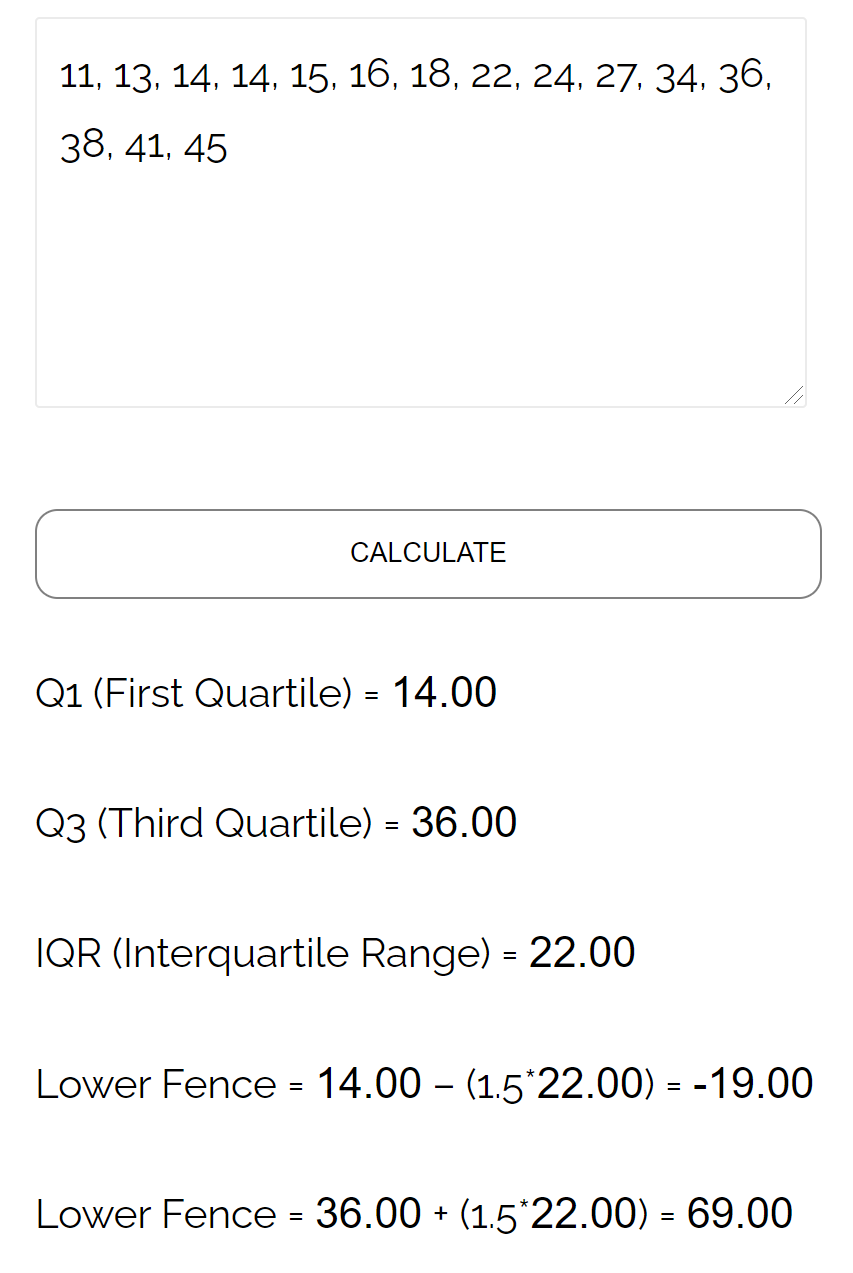
Weitere nützliche Statistikrechner finden Sie auf dieser Seite .