So führen sie eine ols-regression in python durch (mit beispiel)

Die gewöhnliche Regression der kleinsten Quadrate (OLS) ist eine Methode, mit der wir eine Linie finden können, die die Beziehung zwischen einer oder mehreren Prädiktorvariablen und einer Antwortvariablen am besten beschreibt.

Mit dieser Methode können wir die folgende Gleichung finden:

ŷ = b ₀ + b ₁ x

Gold:

• ŷ : Der geschätzte Antwortwert
• b ₀ : Der Ursprung der Regressionslinie
• b ₁ : Die Steigung der Regressionsgeraden

Diese Gleichung kann uns helfen, die Beziehung zwischen dem Prädiktor und der Antwortvariablen zu verstehen, und sie kann verwendet werden, um den Wert einer Antwortvariablen anhand des Werts der Prädiktorvariablen vorherzusagen.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie eine OLS-Regression in Python durchgeführt wird.

Schritt 1: Erstellen Sie die Daten

Für dieses Beispiel erstellen wir einen Datensatz mit den folgenden zwei Variablen für 15 Schüler:

• Gesamtzahl der gelernten Stunden
• Prüfungsergebnis

Wir werden eine OLS-Regression durchführen und dabei Stunden als Prädiktorvariable und Prüfungsergebnis als Antwortvariable verwenden.

Der folgende Code zeigt, wie dieser gefälschte Datensatz in Pandas erstellt wird:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14],
                   ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]})

#view DataFrame
print (df)

    hours score
0 1 64
1 2 66
2 4 76
3 5 73
4 5 74
5 6 81
6 6 83
7 7 82
8 8 80
9 10 88
10 11 84
11 11 82
12 12 91
13 12 93
14 14 89

Schritt 2: Führen Sie eine OLS-Regression durch

Als Nächstes können wir die Funktionen im Statistikmodellmodul verwenden, um eine OLS-Regression durchzuführen, wobei wir Stunden als Prädiktorvariable und Score als Antwortvariable verwenden:

 import statsmodels.api as sm

#define predictor and response variables
y = df[' score ']
x = df[' hours ']

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Fri, 26 Aug 2022 Prob (F-statistic): 2.25e-06
Time: 10:42:24 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================

In der Spalte „coef“ können wir die Regressionskoeffizienten sehen und die folgende angepasste Regressionsgleichung schreiben:

Punktzahl = 65,334 + 1,9824*(Stunden)

Dies bedeutet, dass jede weitere gelernte Stunde mit einer durchschnittlichen Steigerung der Prüfungspunktzahl um 1,9824 Punkte verbunden ist.

Der ursprüngliche Wert von 65.334 gibt uns die durchschnittlich erwartete Prüfungspunktzahl für einen Studenten an, der null Stunden studiert.

Wir können diese Gleichung auch verwenden, um die erwartete Prüfungspunktzahl basierend auf der Anzahl der Stunden, die ein Student studiert, zu ermitteln.

Beispielsweise sollte ein Student, der 10 Stunden lernt, eine Prüfungspunktzahl von 85,158 erreichen:

Punktzahl = 65,334 + 1,9824*(10) = 85,158

So interpretieren Sie den Rest der Modellzusammenfassung:

• P(>|t|): Dies ist der p-Wert, der den Modellkoeffizienten zugeordnet ist. Da der p-Wert für Stunden (0,000) weniger als 0,05 beträgt, können wir sagen, dass ein statistisch signifikanter Zusammenhang zwischen Stunden und Punktzahl besteht.
• R-Quadrat: Dies sagt uns, dass der Prozentsatz der Variation in den Prüfungsergebnissen durch die Anzahl der gelernten Stunden erklärt werden kann. In diesem Fall können 83,1 % der Abweichungen in den Ergebnissen durch die Lernstunden erklärt werden.
• F-Statistik und p-Wert: Die F-Statistik ( 63,91 ) und der entsprechende p-Wert ( 2,25e-06 ) geben Auskunft über die Gesamtsignifikanz des Regressionsmodells, d. h. ob die Prädiktorvariablen im Modell zur Erklärung der Variation nützlich sind. in der Antwortvariablen. Da der p-Wert in diesem Beispiel weniger als 0,05 beträgt, ist unser Modell statistisch signifikant und Stunden werden als nützlich zur Erklärung der Bewertungsvariation angesehen.

Schritt 3: Visualisieren Sie die am besten passende Linie

Schließlich können wir das Datenvisualisierungspaket matplotlib verwenden, um die an die tatsächlichen Datenpunkte angepasste Regressionslinie zu visualisieren:

 import matplotlib. pyplot as plt

#find line of best fit
a, b = np. polyfit (df[' hours '], df[' score '], 1 )

#add points to plot
plt. scatter (df[' hours '], df[' score '], color=' purple ')

#add line of best fit to plot
plt. plot (df[' hours '], a*df[' hours ']+b)

#add fitted regression equation to plot
plt. text ( 1 , 90 , 'y = ' + '{:.3f}'.format(b) + ' + {:.3f}'.format(a) + 'x', size= 12 )

#add axis labels
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

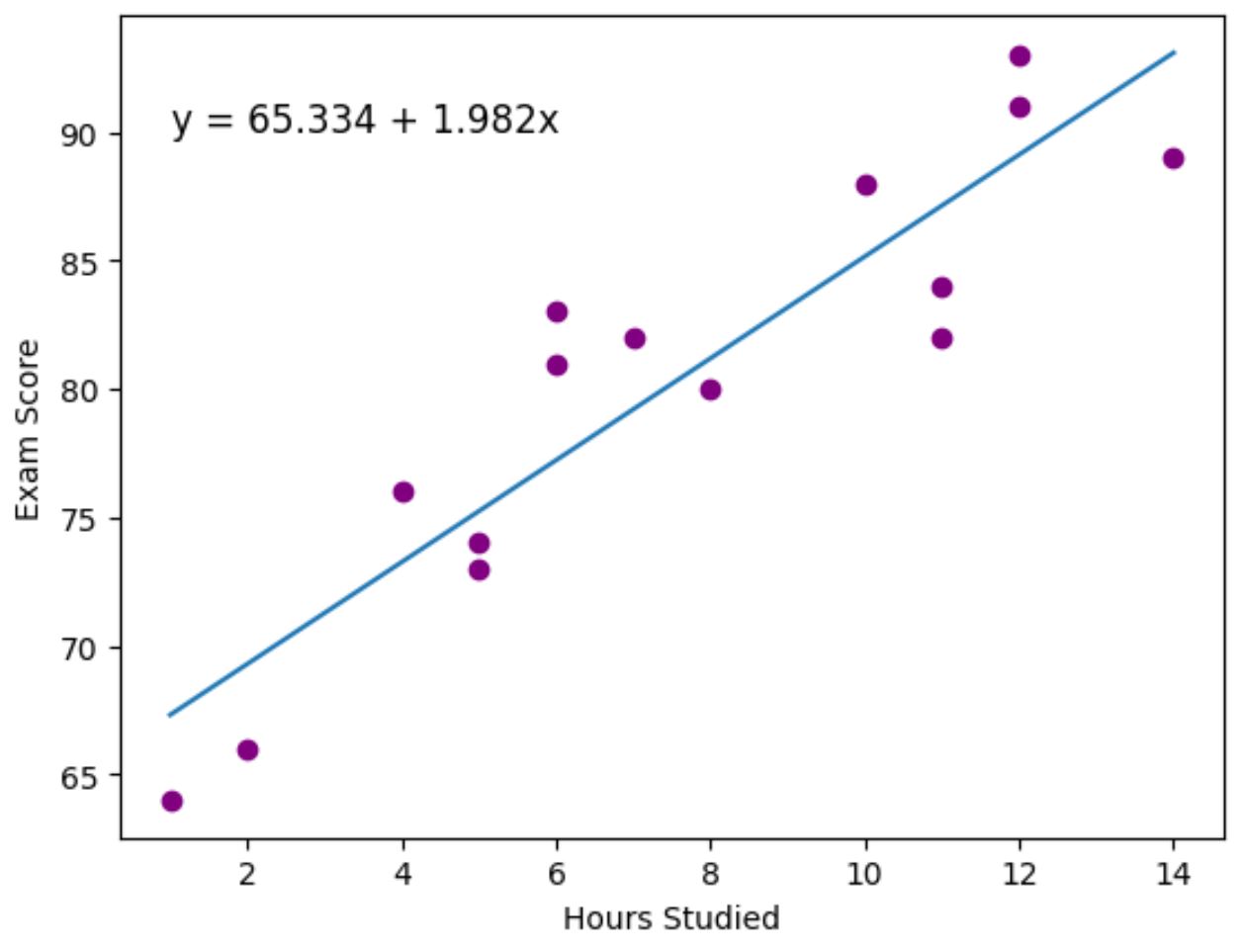
Die violetten Punkte stellen die tatsächlichen Datenpunkte dar und die blaue Linie stellt die angepasste Regressionslinie dar.

Wir haben auch die Funktion plt.text() verwendet, um die angepasste Regressionsgleichung in der oberen linken Ecke des Diagramms hinzuzufügen.

Wenn man sich das Diagramm ansieht, scheint es, dass die angepasste Regressionslinie die Beziehung zwischen der Variablen „ Stunden “ und der Variable „ Score“ recht gut erfasst.

Zusätzliche Ressourcen

Die folgenden Tutorials erklären, wie Sie andere häufige Aufgaben in Python ausführen:

So führen Sie eine logistische Regression in Python durch
So führen Sie eine exponentielle Regression in Python durch
So berechnen Sie den AIC von Regressionsmodellen in Python