Was ist die zuverlässigkeit paralleler formen? (definition & #038; beispiel)

In der Statistik misst die Zuverlässigkeit paralleler Formen die Korrelation zwischen zwei äquivalenten Formen eines Tests.

Der Prozess zur Berechnung der Zuverlässigkeit paralleler Formen ist wie folgt:

Schritt 1: Teilen Sie einen Test in zwei Hälften.

Teilen Sie beispielsweise einen Test mit 100 Fragen nach dem Zufallsprinzip in einen Test A mit 50 Fragen und einen Test B mit ebenfalls 50 Fragen auf.

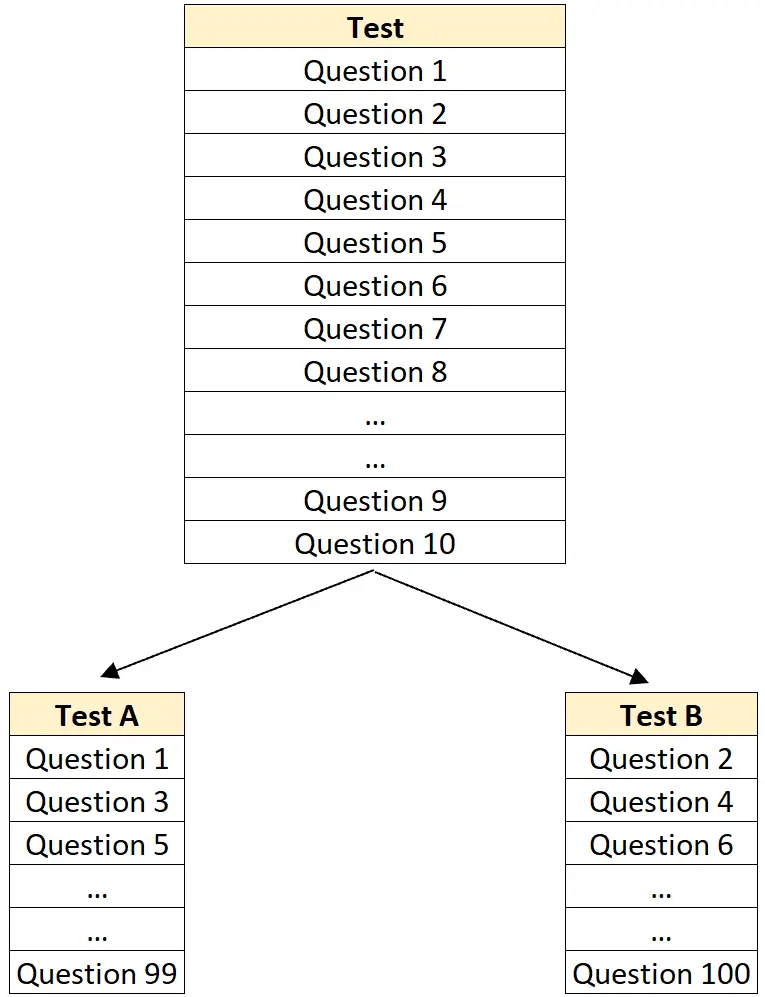
Schritt 2: Verteilen Sie die erste Hälfte an alle Schüler und anschließend die zweite Hälfte an alle Schüler.

Führen Sie beispielsweise Test A für alle 20 Schüler einer bestimmten Klasse durch und notieren Sie deren Ergebnisse. Führen Sie dann, vielleicht einen Monat später, Test B bei denselben 20 Schülern durch und notieren Sie auch deren Ergebnisse bei diesem Test.

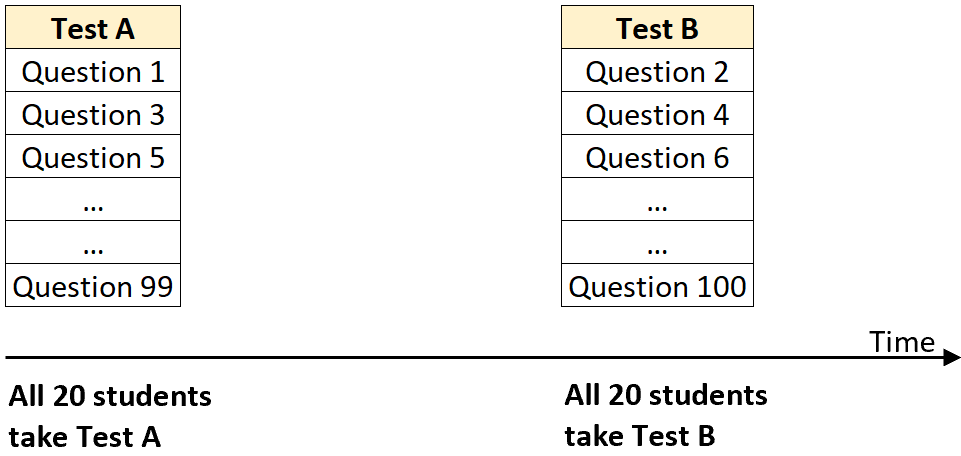
Schritt 3: Berechnen Sie die Korrelation zwischen den Testergebnissen für die beiden Tests.

Berechnen Sie die Korrelation zwischen den Ergebnissen der beiden Tests. Ein Test weist eine Parallelformzuverlässigkeit auf, wenn die Korrelation zwischen den Ergebnissen hoch ist.

Wann sollte die Zuverlässigkeit paralleler Formulare verwendet werden?

Parallele Formularzuverlässigkeit wird häufig im akademischen Umfeld eingesetzt, wenn ein Professor nicht möchte, dass Studierende vorab Zugriff auf Testfragen haben.

Wenn der Professor beispielsweise zu Beginn des Semesters Test A an alle Studierenden verteilt und dann am Ende des Semesters denselben Test A verteilt, können sich die Studierenden die Fragen und Antworten des ersten Tests einfach merken.

Indem der Professor jedoch am Ende des Semesters einen anderen B-Test (und hoffentlich mit gleichem Schwierigkeitsgrad) aushändigt, kann er das Wissen der Studierenden beurteilen und gleichzeitig sicherstellen, dass die Studierenden die Fragen noch nicht gesehen haben.

Mögliche Nachteile der Zuverlässigkeit paralleler Formulare

Die Zuverlässigkeit paralleler Formen hat zwei potenzielle Nachteile:

1. Es erfordert viele Fragen.

Die Zuverlässigkeit paralleler Formulare eignet sich am besten für Tests mit einer großen Anzahl von Fragen (z. B. 100 Fragen), da die Zahl, die wir für die Korrelation berechnen, zuverlässiger ist.

2. Es gibt keine Garantie dafür, dass die beiden Hälften tatsächlich parallel sind.

Wenn wir einen Test zufällig in zwei Hälften aufteilen, gibt es keine Garantie dafür, dass die beiden Hälften tatsächlich parallel oder „gleich“ im Schwierigkeitsgrad sind. Dies bedeutet, dass die Ergebnisse zwischen den beiden Tests unterschiedlich sein können, einfach weil sich eine Hälfte als schwieriger erweist als die andere.

Zuverlässigkeit paralleler Formulare und Split-Half-Zuverlässigkeit

Die Zuverlässigkeit paralleler Formen ähnelt der halbierten Zuverlässigkeit , es gibt jedoch einen kleinen Unterschied:

Zuverlässigkeit zweigeteilt:

Dabei wird ein Test in zwei Hälften geteilt und jede Hälfte derselben Gruppe von Schülern vorgelegt. Die Reihenfolge, in der die Studierenden den Test absolvieren, spielt keine Rolle.

Der Vorteil dieser Methode besteht darin , die interne Konsistenz zu messen. Idealerweise möchten wir, dass die Korrelation zwischen den Hälften hoch ist, da dies darauf hinweist, dass alle Teile des Tests gleichermaßen zu dem beitragen, was gemessen wird.

Zuverlässigkeit paralleler Formen:

Dabei wird ein Test in zwei Hälften geteilt – mit „A“ und „B“ bezeichnet – und jede Hälfte für dieselbe Gruppe von Schülern durchgeführt.

Es ist jedoch wichtig, dass alle Schüler zuerst den „A“-Test und dann den „B“-Test absolvieren, damit die Kenntnis der Antworten auf den „A“-Test keinen Vorteil für die Schüler bringt, die später den „A“-Test ablegen. B“.

Zusätzliche Ressourcen

Eine kurze Einführung in die Zuverlässigkeitsanalyse
Was ist die halbierte Zuverlässigkeit?
Was ist Test-Retest-Reliabilität?
Was ist Interrater-Reliabilität?