Pareto-verteilung

Von August 3, 2023 Wahrscheinlichkeit Keine Kommentare

In diesem Artikel wird erklärt, was Pareto-Verteilung in der Statistik ist und wofür sie verwendet wird. Sie können auch das Pareto-Verteilungsdiagramm und die Eigenschaften dieser Art von Wahrscheinlichkeitsverteilung sehen.

Was ist Pareto-Verteilung?

Die Pareto-Verteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die in der Statistik zur Modellierung des Pareto-Prinzips verwendet wird. Daher ist die Pareto-Verteilung eine Wahrscheinlichkeitsverteilung, die einige wenige Werte aufweist, deren Eintrittswahrscheinlichkeit viel höher ist als die der übrigen Werte.

Denken Sie daran, dass das Pareto-Gesetz, auch 80-20-Regel genannt, ein statistisches Prinzip ist, das besagt, dass die Ursache eines Phänomens größtenteils auf einen kleinen Teil der Bevölkerung zurückzuführen ist.

Die Pareto-Verteilung hat zwei charakteristische Parameter: den Skalenparameter x m und den Formparameter α.

X\sim \text{Pareto}(\alpha,x_m)

Ursprünglich wurde die Pareto-Verteilung verwendet, um die Vermögensverteilung innerhalb der Bevölkerung zu beschreiben, da der Großteil davon auf einen kleinen Teil der Bevölkerung zurückzuführen war. Doch derzeit hat die Pareto-Verteilung viele Anwendungen, beispielsweise in der Qualitätskontrolle, in der Wirtschaft, in der Wissenschaft, im sozialen Bereich usw.

Die Pareto-Verteilung ist nach dem Ökonomen Vilfredo Pareto benannt, der die Verteilung formuliert hat. Am bekanntesten ist er jedoch für das Pareto-Diagramm.

Pareto-Verteilungstabelle

Nachdem wir nun die Definition der Pareto-Verteilung kennen, schauen wir uns einige Beispiele für Pareto-Verteilungen an, die grafisch dargestellt werden.

Unten sehen Sie also, wie der Graph der Dichtefunktion der Pareto-Verteilung in Abhängigkeit von seinen charakteristischen Werten aussieht:

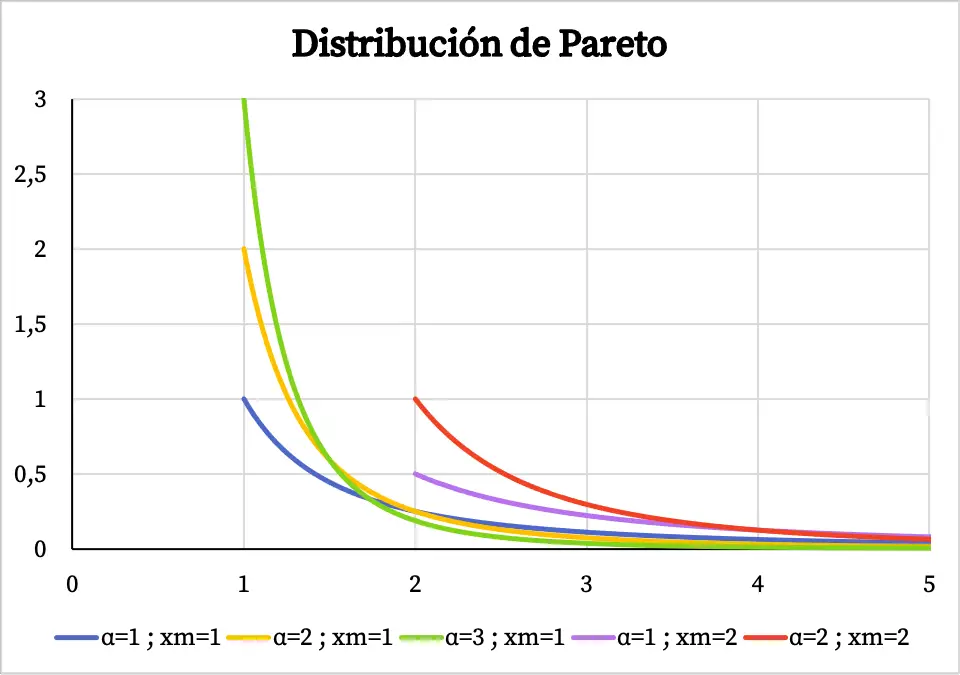
Pareto-Verteilungsdiagramm

Beachten Sie, dass der Bereich der Pareto-Verteilung vom Wert x m bis +∞ reicht, weshalb die Dichtefunktion nicht vor dem Wert x m existiert.

Andererseits sieht der Graph der kumulativen Wahrscheinlichkeitsfunktion der Pareto-Verteilung wie folgt aus:

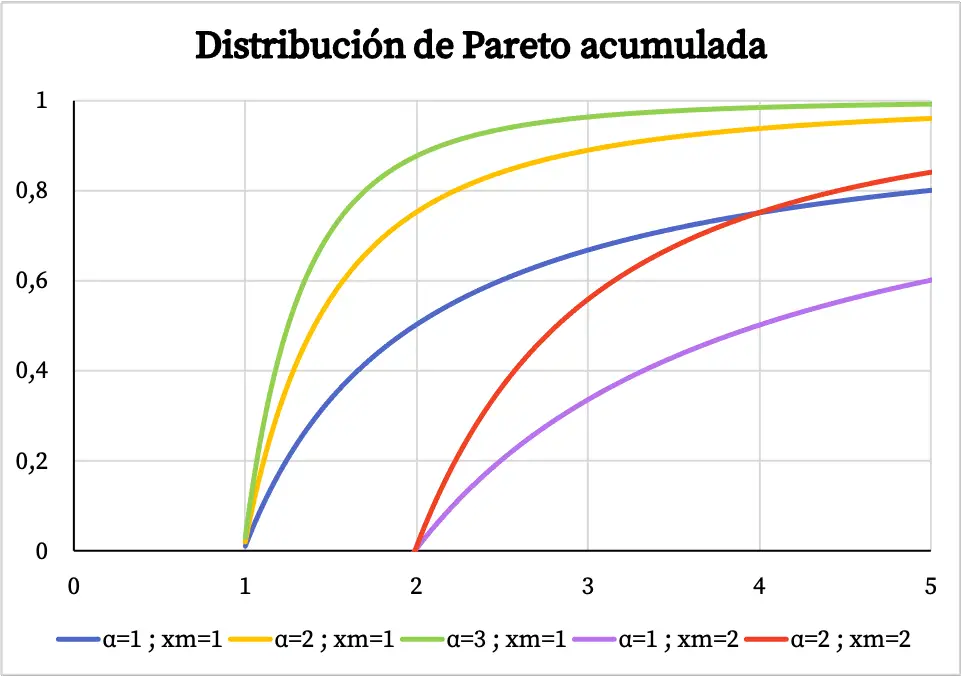
kumulative Wahrscheinlichkeit der Pareto-Verteilung

Merkmale der Pareto-Verteilung

Nachfolgend sind die wichtigsten Merkmale der Pareto-Verteilung im Zusammenhang mit Wahrscheinlichkeitstheorie und Statistik aufgeführt.

  • Die Pareto-Verteilung hat zwei charakteristische Parameter, die ihre Kurve definieren: den Skalenparameter x m und den Formparameter α.

X\sim \text{Pareto}(\alpha,x_m)

  • Der Bereich der Pareto-Verteilung besteht aus allen reellen Zahlen vom Skalenparameter bis plus Unendlich.

x\in [x_m,+\infty)

  • Wenn α größer als 1 ist, ist der Mittelwert der Pareto-Verteilung gleich dem Produkt aus α mal x m und α minus 1.

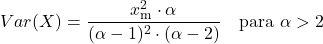
E[X]=\cfrac{\alpha\cdot x_m}{\alpha-1}\quad\text{para } \alpha>1″ title=“Rendered by QuickLaTeX.com“ height=“34″ width=“214″ style=“vertical-align: -12px;“></p> </p> <ul> <li> Die Varianz der Pareto-Verteilung hängt von den beiden charakteristischen Parametern der Verteilung ab und wird mit der folgenden Formel berechnet:</li> </ul> <p class=\displaystyle Var(X)=\frac{x_\mathrm{m}^2\cdot \alpha}{(\alpha-1)^2\cdot(\alpha-2)}\quad \text{para }\alpha>2″ title=“Rendered by QuickLaTeX.com“ height=“44″ width=“323″ style=“vertical-align: -17px;“></p> </p> <ul> <li> Der Median der Pareto-Verteilung kann mit dem folgenden Ausdruck bestimmt werden:</li> </ul> <p class=\displaystyle Me=x_\mathrm{m}\cdot \sqrt[\alpha]{2}

  • Der Modus der Pareto-Verteilung entspricht dem Skalenparameter x m der Verteilung.

Mo=x_m

  • Die Formel für die Dichtefunktion der Pareto-Verteilung lautet:

\displaystyle P[X=x]=\frac{\alpha\cdot x_m^\alpha}{x^{\alpha+1}}\quad\text{para }x\geq x_m

  • Ebenso lautet die Formel für die kumulative Wahrscheinlichkeitsfunktion der Pareto-Verteilung:

\displaystyle P[X\leq x]=1-\left(\frac{x_\mathrm{m}}{x}\right)^\alpha

  • Der Asymmetriekoeffizient der Pareto-Verteilung hängt nur vom Formparameter α ab und sein Ausdruck lautet:

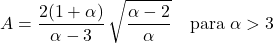
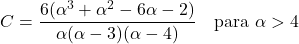
\displaystyle A=\frac{2(1+\alpha)}{\alpha-3}\,\sqrt{\frac{\alpha-2}{\alpha}}\quad\text{para }\alpha>3″ title=“Rendered by QuickLaTeX.com“ height=“43″ width=“274″ style=“vertical-align: -14px;“></p> </p> <ul> <li> Der Kurtosis-Koeffizient der Pareto-Verteilung variiert auch abhängig vom Wert des Parameters α und wird nach der folgenden Formel berechnet:</li> </ul> <p class=\displaystyle C=\frac{6(\alpha^3+\alpha^2-6\alpha-2)}{\alpha(\alpha-3)(\alpha-4)}\quad\text{para }\alpha>4″ title=“Rendered by QuickLaTeX.com“ height=“44″ width=“299″ style=“vertical-align: -17px;“></p></p> </div><!-- End Content --> <!-- Start Author Box --> <div class=

Über den Autor

Benjamin Anderson
Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen

Einen Kommentar hinzufügen

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert