Partielle kleinste quadrate in r (schritt für schritt)
Eines der häufigsten Probleme beim maschinellen Lernen ist die Multikollinearität . Dies tritt auf, wenn zwei oder mehr Prädiktorvariablen in einem Datensatz stark korrelieren.
Wenn dies geschieht, kann ein Modell möglicherweise gut an einen Trainingsdatensatz angepasst werden, bei einem neuen Datensatz, den es noch nie gesehen hat, kann es jedoch eine schlechte Leistung erbringen, da es zu stark an den Trainingsdatensatz angepasst ist . Trainingsset.
Eine Möglichkeit, dieses Problem zu umgehen, besteht darin, eine Methode namens „partielle kleinste Quadrate“ zu verwenden, die wie folgt funktioniert:
- Prädiktor- und Antwortvariablen standardisieren.
- Berechnen Sie M lineare Kombinationen (sogenannte „PLS-Komponenten“) der p ursprünglichen Prädiktorvariablen, die eine signifikante Variation sowohl in der Antwortvariablen als auch in den Prädiktorvariablen erklären.
- Verwenden Sie die Methode der kleinsten Quadrate, um ein lineares Regressionsmodell anzupassen, wobei die PLS-Komponenten als Prädiktoren verwendet werden.
- Verwenden Sie die k-fache Kreuzvalidierung, um die optimale Anzahl von PLS-Komponenten zu finden, die im Modell beibehalten werden sollen.
Dieses Tutorial bietet ein schrittweises Beispiel für die Berechnung partieller kleinster Quadrate in R.
Schritt 1: Laden Sie die erforderlichen Pakete
Der einfachste Weg, partielle kleinste Quadrate in R durchzuführen, ist die Verwendung von Funktionen im pls- Paket.
#install pls package (if not already installed) install.packages(" pls ") load pls package library(pls)
Schritt 2: Passen Sie das Modell der partiellen kleinsten Quadrate an
Für dieses Beispiel verwenden wir den integrierten R-Datensatz namens mtcars , der Daten zu verschiedenen Fahrzeugtypen enthält:
#view first six rows of mtcars dataset
head(mtcars)
mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3,460 20.22 1 0 3 1
Für dieses Beispiel passen wir ein Modell der partiellen kleinsten Quadrate (PLS) an, wobei wir hp als Antwortvariable und die folgenden Variablen als Prädiktorvariablen verwenden:
- mpg
- Anzeige
- Scheisse
- Gewicht
- qsec
Der folgende Code zeigt, wie das PLS-Modell an diese Daten angepasst wird. Beachten Sie die folgenden Argumente:
- scale=TRUE : Dies teilt R mit, dass jede der Variablen im Datensatz so skaliert werden soll, dass sie einen Mittelwert von 0 und eine Standardabweichung von 1 aufweist. Dadurch wird sichergestellt, dass keine Prädiktorvariable einen zu großen Einfluss auf das Modell hat, wenn sie in verschiedenen Einheiten gemessen wird.
- validation=“CV“ : Dies weist R an , die k-fache Kreuzvalidierung zu verwenden, um die Modellleistung zu bewerten. Beachten Sie, dass hierbei standardmäßig k=10 Falten verwendet werden. Beachten Sie außerdem, dass Sie stattdessen „LOOCV“ angeben können, um eine Leave-One-Out-Kreuzvalidierung durchzuführen.
#make this example reproducible set.seed(1) #fit PCR model model <- plsr(hp~mpg+disp+drat+wt+qsec, data=mtcars, scale= TRUE , validation=" CV ")
Schritt 3: Wählen Sie die Anzahl der PLS-Komponenten
Sobald wir das Modell angepasst haben, müssen wir bestimmen, wie viele PLS-Komponenten wir behalten möchten.
Schauen Sie sich dazu einfach den quadratischen Mittelfehler des Tests (Test-RMSE) an, der durch die K-Kreuzvalidierung berechnet wurde:
#view summary of model fitting
summary(model)
Data:
Y dimension: 32 1
Fit method: kernelpls
Number of components considered: 5
VALIDATION: RMSEP
Cross-validated using 10 random segments.
(Intercept) 1 comp 2 comps 3 comps 4 comps 5 comps
CV 69.66 40.57 35.48 36.22 36.74 36.67
adjCV 69.66 40.41 35.12 35.80 36.27 36.20
TRAINING: % variance explained
1 comp 2 comps 3 comps 4 comps 5 comps
X 68.66 89.27 95.82 97.94 100.00
hp 71.84 81.74 82.00 82.02 82.03
Das Ergebnis enthält zwei interessante Tabellen:
1. VALIDIERUNG: RMSEP
Diese Tabelle zeigt uns den RMSE-Test, der durch k-fache Kreuzvalidierung berechnet wurde. Wir können Folgendes sehen:
- Wenn wir im Modell nur den ursprünglichen Term verwenden, beträgt der RMSE des Tests 69,66 .
- Wenn wir die erste PLS-Komponente hinzufügen, sinkt der RMSE-Test auf 40,57.
- Wenn wir die zweite PLS-Komponente hinzufügen, sinkt der RMSE-Test auf 35,48.
Wir können sehen, dass das Hinzufügen zusätzlicher PLS-Komponenten tatsächlich zu einer Erhöhung des RMSE des Tests führt. Daher scheint es optimal zu sein, im endgültigen Modell nur zwei PLS-Komponenten zu verwenden.
2. TRAINING: % der erklärten Varianz
Diese Tabelle zeigt uns den Prozentsatz der Varianz in der Antwortvariablen, die durch die PLS-Komponenten erklärt wird. Wir können Folgendes sehen:
- Wenn wir nur die erste PLS-Komponente verwenden, können wir 68,66 % der Variation der Antwortvariablen erklären.
- Durch Hinzufügen der zweiten PLS-Komponente können wir 89,27 % der Variation der Antwortvariablen erklären.
Beachten Sie, dass wir immer noch in der Lage sein werden, mehr Varianz durch die Verwendung von mehr PLS-Komponenten zu erklären, aber wir können sehen, dass das Hinzufügen von mehr als zwei PLS-Komponenten den Prozentsatz der erklärten Varianz nicht wesentlich erhöht.
Wir können den RMSE-Test (zusammen mit MSE und R-Quadrat-Test) auch als Funktion der Anzahl der PLS-Komponenten mithilfe der Funktion validationplot() visualisieren.
#visualize cross-validation plots validationplot(model) validationplot(model, val.type=" MSEP ") validationplot(model, val.type=" R2 ")
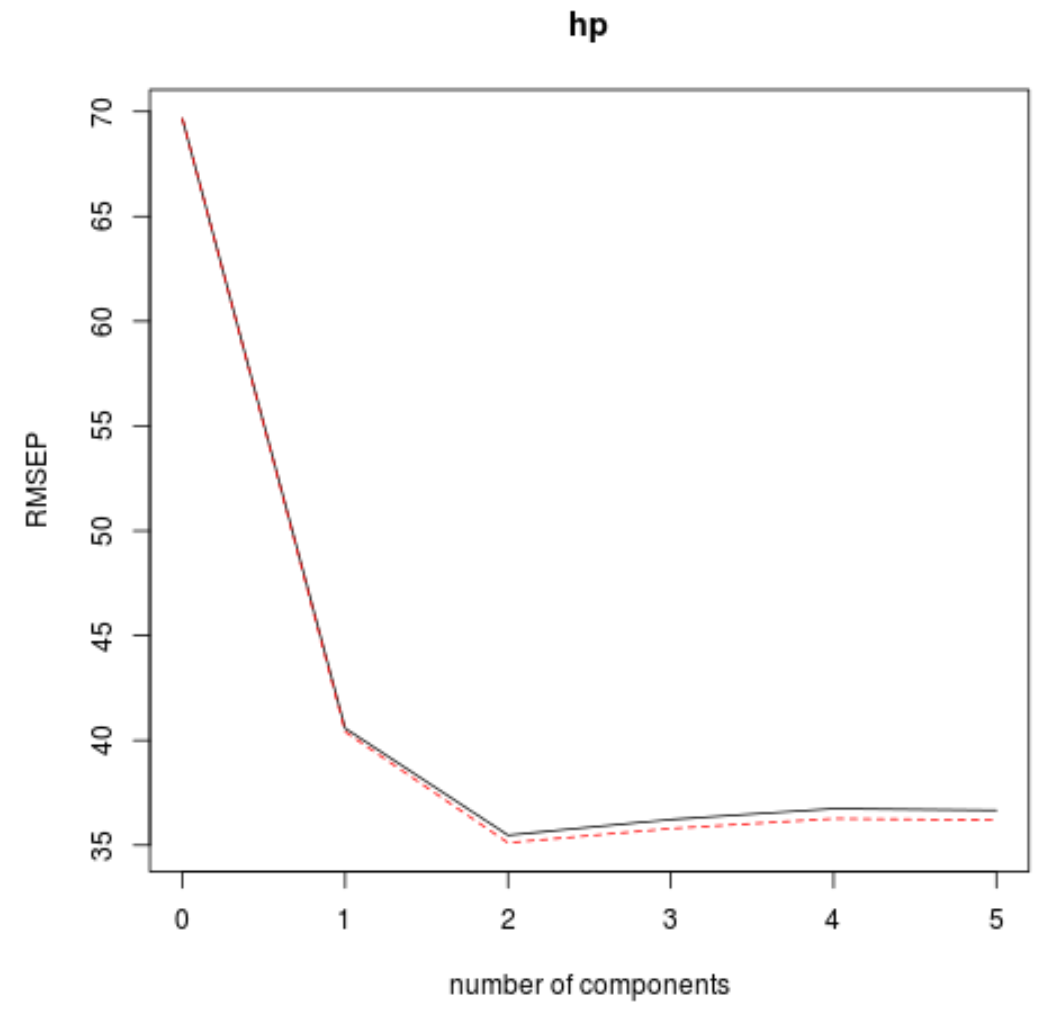
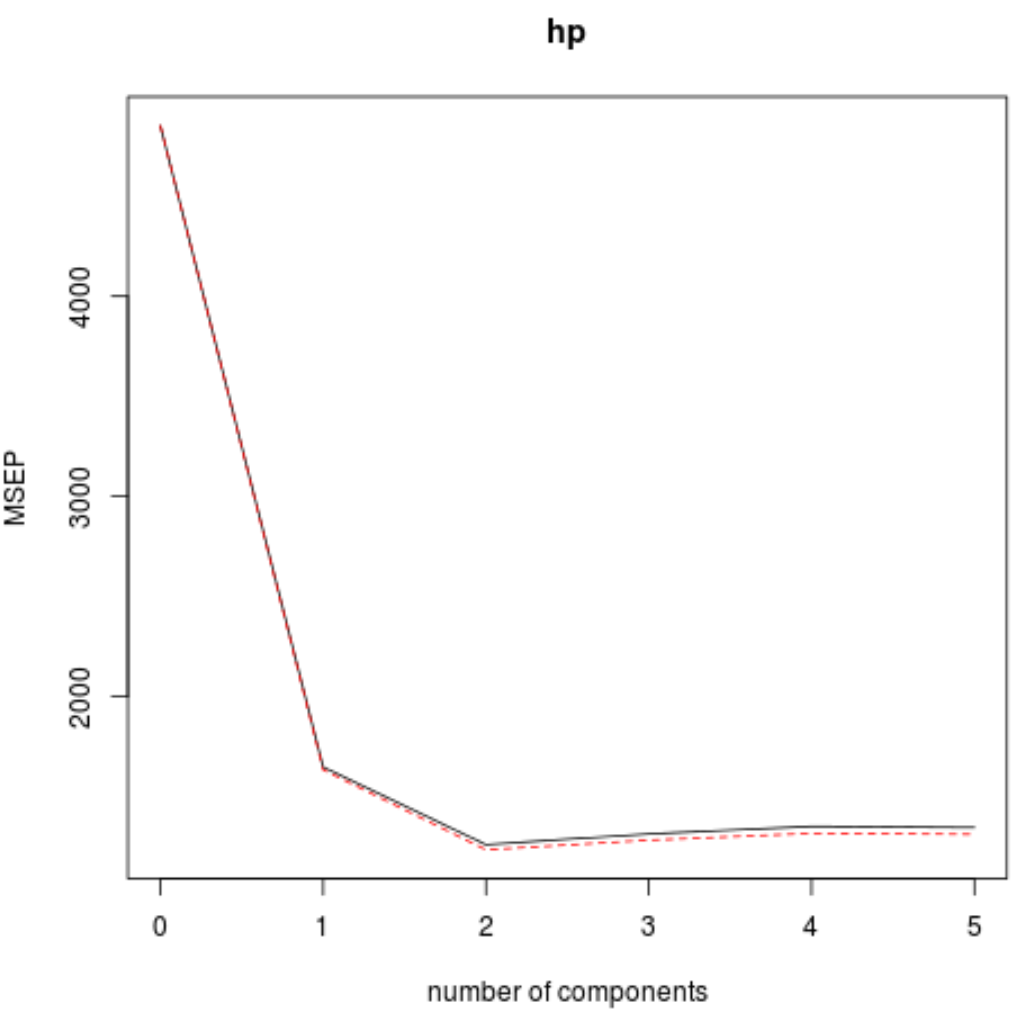
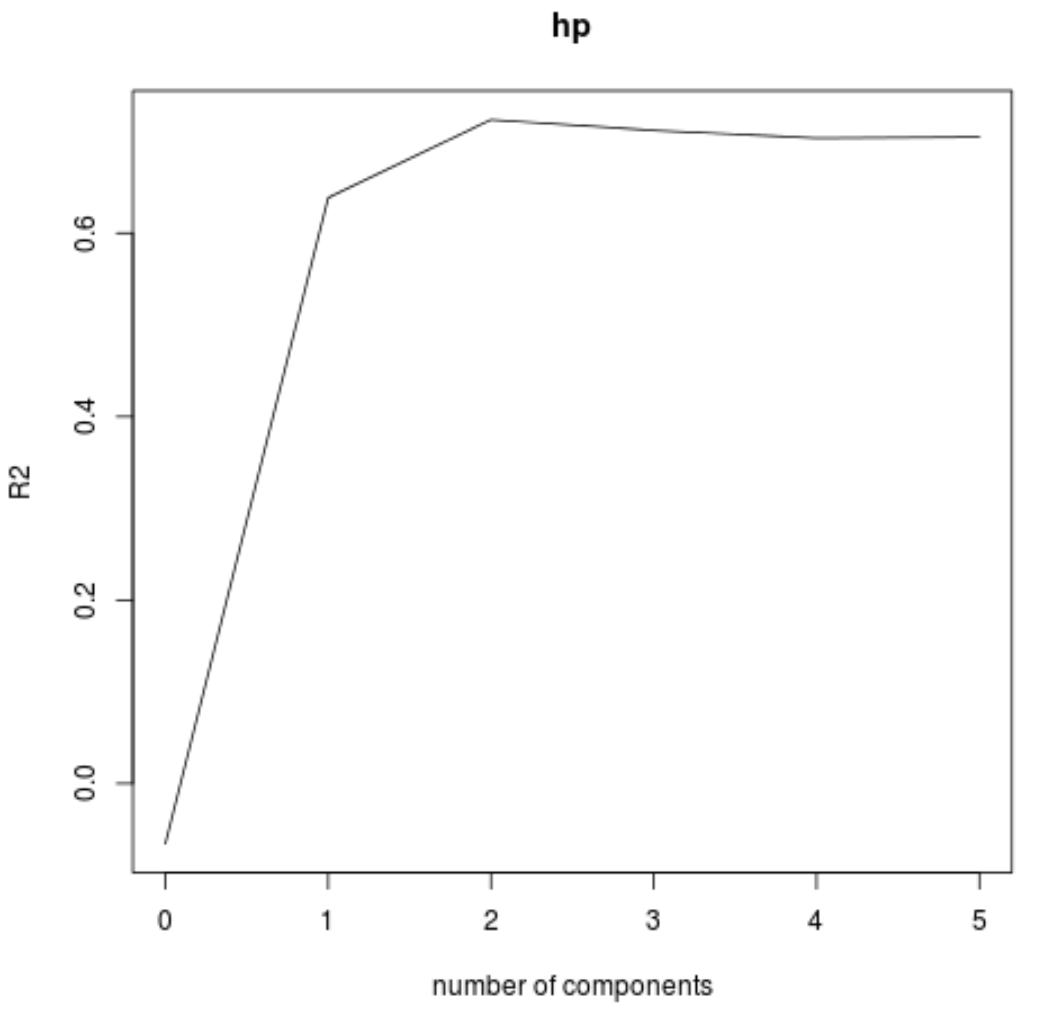
In jedem Diagramm können wir sehen, dass sich die Modellanpassung durch das Hinzufügen von zwei PLS-Komponenten verbessert, sich jedoch tendenziell verschlechtert, wenn wir weitere PLS-Komponenten hinzufügen.
Somit umfasst das optimale Modell nur die ersten beiden PLS-Komponenten.
Schritt 4: Verwenden Sie das endgültige Modell, um Vorhersagen zu treffen
Wir können das endgültige Modell mit zwei PLS-Komponenten verwenden, um Vorhersagen über neue Beobachtungen zu treffen.
Der folgende Code zeigt, wie Sie den Originaldatensatz in einen Trainings- und einen Testsatz aufteilen und das endgültige Modell mit zwei PLS-Komponenten verwenden, um Vorhersagen für den Testsatz zu treffen.
#define training and testing sets train <- mtcars[1:25, c("hp", "mpg", "disp", "drat", "wt", "qsec")] y_test <- mtcars[26: nrow (mtcars), c("hp")] test <- mtcars[26: nrow (mtcars), c("mpg", "disp", "drat", "wt", "qsec")] #use model to make predictions on a test set model <- plsr(hp~mpg+disp+drat+wt+qsec, data=train, scale= TRUE , validation=" CV ") pcr_pred <- predict(model, test, ncomp= 2 ) #calculate RMSE sqrt ( mean ((pcr_pred - y_test)^2)) [1] 54.89609
Wir sehen, dass der RMSE des Tests 54,89609 beträgt. Dies ist die durchschnittliche Abweichung zwischen dem vorhergesagten HP- Wert und dem beobachteten HP- Wert für die Testsatzbeobachtungen.
Beachten Sie, dass ein äquivalentes Hauptkomponenten-Regressionsmodell mit zwei Hauptkomponenten einen Test-RMSE von 56,86549 ergab. Somit übertraf das PLS-Modell das PCR-Modell für diesen Datensatz leicht.
Die vollständige Verwendung des R-Codes in diesem Beispiel finden Sie hier .