So erstellen sie partielle residuendiagramme in r

Die multiple lineare Regression ist eine statistische Methode, mit der wir die Beziehung zwischen mehreren Prädiktorvariablen und einer Antwortvariablen verstehen können.

Eine der wichtigsten Annahmen der multiplen linearen Regression ist jedoch, dass zwischen jeder Prädiktorvariablen und der Antwortvariablen eine lineare Beziehung besteht.

Wenn diese Annahme nicht erfüllt ist, sind die Ergebnisse des Regressionsmodells möglicherweise nicht zuverlässig.

Eine Möglichkeit, diese Annahme zu testen, besteht darin, ein Diagramm mit partiellen Residuen zu erstellen, das die Residuen einer Prädiktorvariablen relativ zur Antwortvariablen anzeigt.

Das folgende Beispiel zeigt, wie man partielle Residuendiagramme für ein Regressionsmodell in R erstellt.

Beispiel: So erstellen Sie partielle Residuendiagramme in R

Angenommen, wir passen ein Regressionsmodell mit drei Prädiktorvariablen in R an:

 #make this example reproducible
set. seeds (0)

#define response variable
y <- c(1:1000)

#define three predictor variables
x1 <- c(1:1000)*runif(n=1000)
x2 <- (c(1:1000)*rnorm(n=1000))^2
x3 <- (c(1:1000)*rnorm(n=1000))^3

#fit multiple linear regression model
model <- lm(y~x1+x2+x3))

Wir können die Funktion crPlots() aus dem Paket car in R verwenden, um partielle Residuendiagramme für jede Prädiktorvariable im Modell zu erstellen:

 library (car)

#create partial residual plots
crPlots(model)

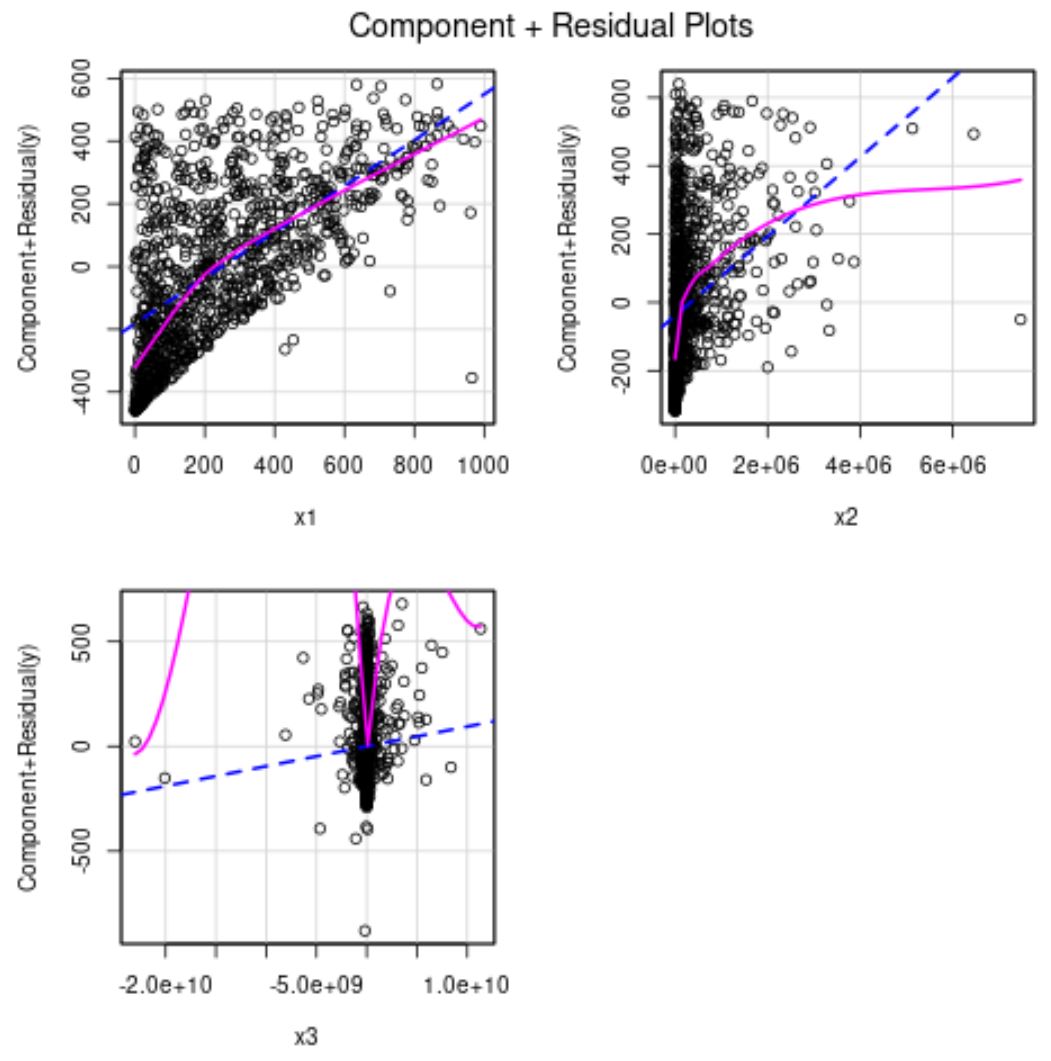
Die blaue Linie zeigt die erwarteten Residuen, wenn die Beziehung zwischen dem Prädiktor und der Antwortvariablen linear wäre. Die rosa Linie zeigt die tatsächlichen Residuen.

Wenn sich die beiden Linien deutlich unterscheiden, deutet dies auf einen nichtlinearen Zusammenhang hin.

Aus den obigen Grafiken können wir ersehen, dass die Residuen für x2 und x3 nichtlinear erscheinen.

Dies verstößt gegen die Linearitätsannahme der multiplen linearen Regression. Eine Möglichkeit, dieses Problem zu lösen, besteht darin, eine Quadrat- oder Kubikwurzeltransformation für die Prädiktorvariablen zu verwenden:

 library (car)

#fit new model with transformed predictor variables
model_transformed <- lm(y~x1+sqrt(x2)+log10(x3^(1/3)))

#create partial residual plots for new model
crPlots(model_transformed)

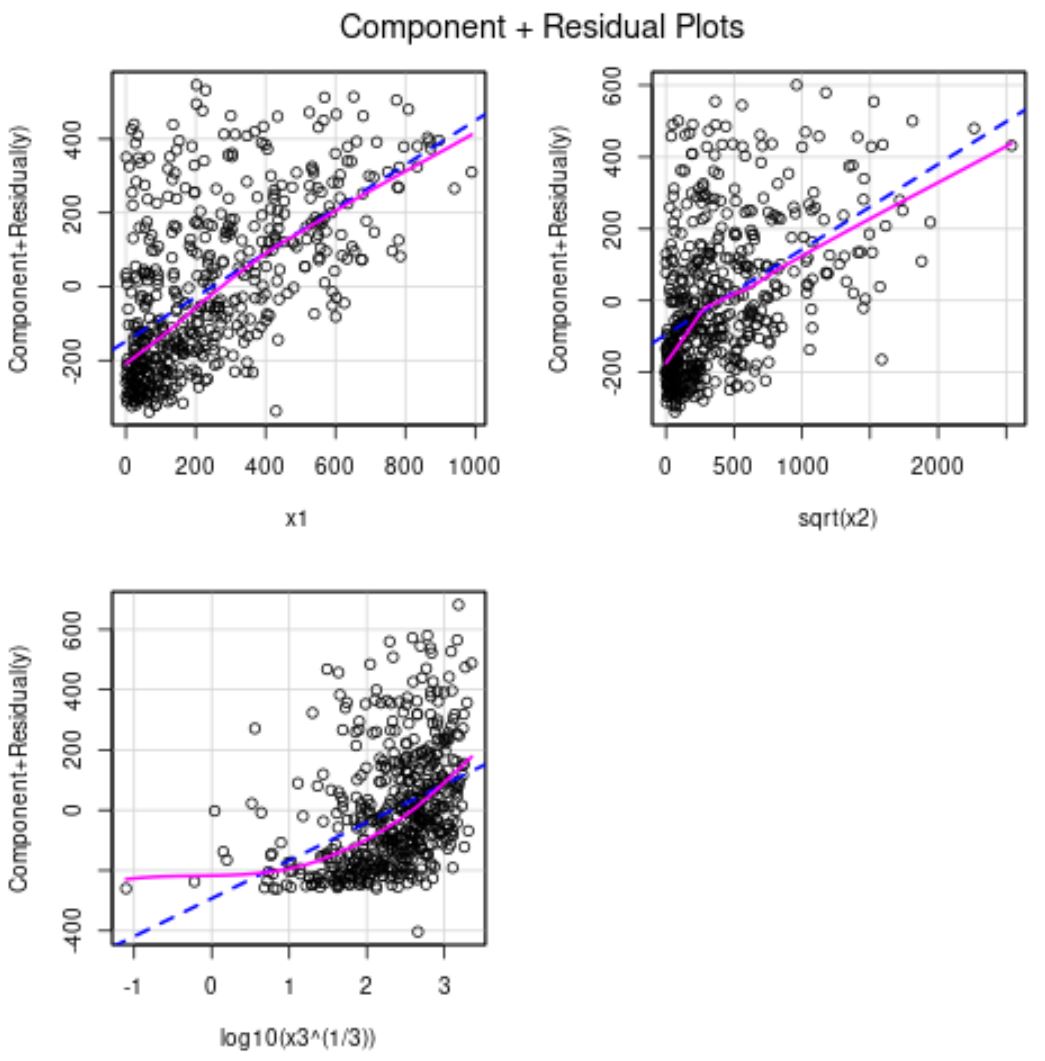
Aus den partiellen Residuendiagrammen können wir erkennen, dass x2 jetzt eine linearere Beziehung zur Antwortvariablen hat.

Die x3-Prädiktorvariable ist immer noch etwas nichtlinear, daher entscheiden wir uns möglicherweise für eine andere Transformation oder entfernen die Variable möglicherweise ganz aus dem Modell.

Zusätzliche Ressourcen

Die folgenden Tutorials erklären, wie man andere gängige Diagramme in R erstellt:

So erstellen Sie Diagnosediagramme in R
So erstellen Sie ein Maßstabs- und Standortdiagramm in R
So erstellen Sie ein Residuendiagramm in R