Pearsons schiefekoeffizient in excel (schritt für schritt)

Der vom Biostatistiker Karl Pearson entwickelte Pearson-Skewness-Koeffizient ist eine Möglichkeit, die Schiefe in einem Beispieldatensatz zu messen.

Es gibt tatsächlich zwei Methoden, die zur Berechnung des Pearson-Skewness-Koeffizienten verwendet werden können:

Methode 1: Modus verwenden

Schiefe = (Mittelwert – Modus) / Stichprobenstandardabweichung

Methode 2: Verwendung des Medians

Schiefe = 3 (Mittelwert – Median) / Stichprobenstandardabweichung

Im Allgemeinen wird die zweite Methode bevorzugt, da der Modus nicht immer ein guter Hinweis darauf ist, wo der „zentrale“ Wert eines Datensatzes liegt und es möglicherweise mehr als einen Modus in einem angegebenen Datensatz gibt.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie beide Versionen des Pearson-Skewness-Koeffizienten für einen bestimmten Datensatz in Excel berechnet werden.

Schritt 1: Erstellen Sie den Datensatz

Erstellen wir zunächst den folgenden Datensatz in Excel:

Schritt 2: Berechnen Sie den Pearson-Schiefekoeffizienten (mit dem Modus)

Dann können wir die folgende Formel verwenden, um den Pearson-Skewness-Koeffizienten mithilfe des Modus zu berechnen:

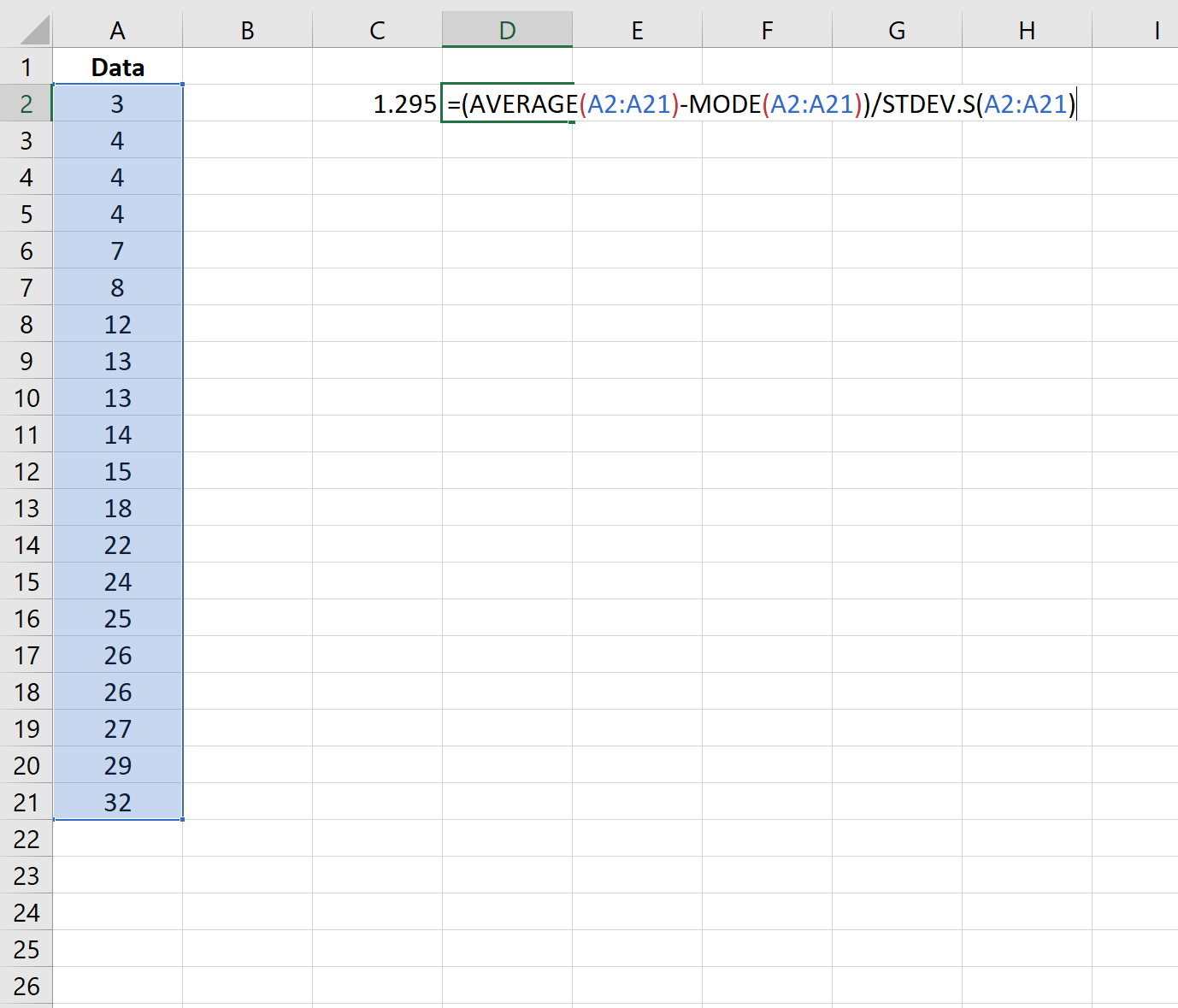
Die Schiefe beträgt 1,295 .

Schritt 3: Berechnen Sie den Pearson-Skewness-Koeffizienten (unter Verwendung des Medians)

Wir können auch die folgende Formel verwenden, um den Pearson-Skewness-Koeffizienten mithilfe des Medians zu berechnen:

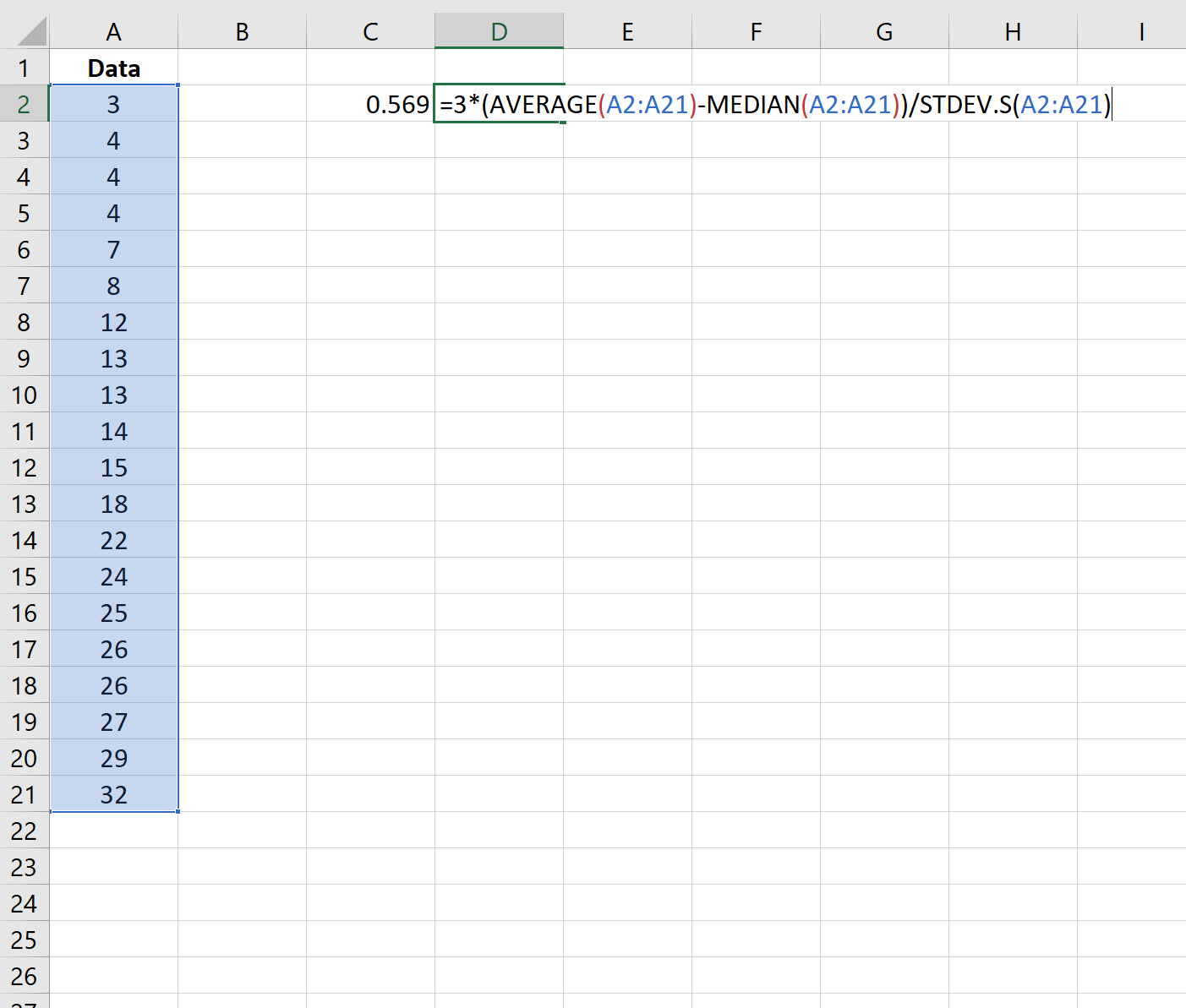
Die Asymmetrie beträgt 0,569 .

Wie man Asymmetrie interpretiert

Wir interpretieren den Pearson-Asymmetriekoeffizienten auf folgende Weise:

• Ein Wert von 0 bedeutet keine Asymmetrie. Wenn wir ein Histogramm erstellen würden, um die Werteverteilung in einem Datensatz zu visualisieren, wäre es vollkommen symmetrisch.
• Ein positiver Wert zeigt eine positive Neigung oder „rechte“ Neigung an. Ein Histogramm würde einen „Schwanz“ auf der rechten Seite der Verteilung erkennen lassen.
• Ein negativer Wert zeigt eine negative Neigung oder Neigung nach „links“ an. Ein Histogramm würde einen „Schwanz“ auf der linken Seite der Verteilung erkennen lassen.

In unserem vorherigen Beispiel war die Schiefe positiv, was darauf hinweist, dass die Verteilung der Datenwerte positiv schief oder „richtig“ war.

Zusätzliche Ressourcen

In diesem Artikel finden Sie eine schöne Erklärung der links- und rechtsschiefen Verteilungen.