Die fünf hypothesen der pearson-korrelation

Der Pearson-Korrelationskoeffizient (auch als „Produkt-Moment-Korrelationskoeffizient“ bekannt) misst den linearen Zusammenhang zwischen zwei Variablen.

Es nimmt immer einen Wert zwischen -1 und 1 an, wobei:

• -1 zeigt eine vollkommen negative lineare Korrelation zwischen zwei Variablen an
• 0 bedeutet, dass zwischen zwei Variablen keine lineare Korrelation besteht
• 1 zeigt eine vollkommen positive lineare Korrelation zwischen zwei Variablen an

Bevor wir jedoch den Pearson-Korrelationskoeffizienten zwischen zwei Variablen berechnen, müssen wir sicherstellen, dass fünf Annahmen erfüllt sind:

1. Messebene: Beide Variablen sollten auf Intervall- oder Verhältnisebene gemessen werden.

2. Lineare Beziehung: Zwischen den beiden Variablen muss eine lineare Beziehung bestehen.

3. Normalität: Beide Variablen sollten annähernd normalverteilt sein.

4. Verwandte Paare: Jede Beobachtung im Datensatz muss ein Wertepaar haben.

5. Keine Ausreißer: Der Datensatz sollte keine extremen Ausreißer enthalten.

In diesem Artikel erläutern wir jede Annahme und erläutern, wie Sie feststellen können, ob die Annahme erfüllt ist.

Hypothese 1: Messebene

Um einen Pearson-Korrelationskoeffizienten zwischen zwei Variablen zu berechnen, müssen beide Variablen auf Intervall- oder Verhältnisebene gemessen werden.

Die folgende Grafik bietet eine kurze Erklärung der vier Ebenen, auf denen Variablen gemessen werden können:

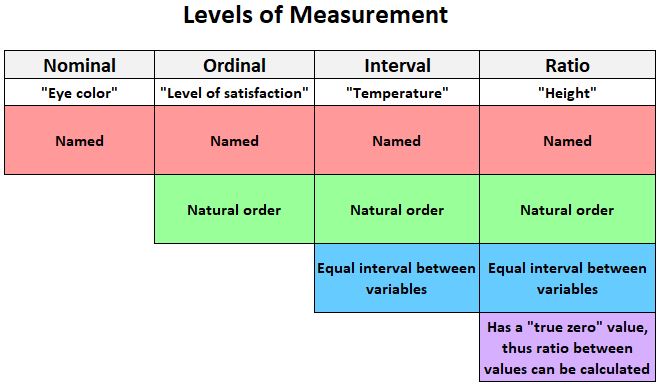
Hier sind einige Beispiele für Variablen, die auf einer Intervallskala gemessen werden können:

• Temperatur: Gemessen in Fahrenheit oder Celsius
• Kredit-Scores: gemessen von 300 bis 850
• SAT-Ergebnisse: gemessen zwischen 400 und 1.600

Hier sind einige Beispiele für Variablen, die auf einer Verhältnisskala gemessen werden können:

• Größe: Gemessen in Zentimetern, Zoll, Fuß usw.
• Gewicht: gemessen in Kilogramm, Pfund usw.
• Länge: Gemessen in Zentimetern, Zoll, Fuß usw.

Wenn die Variablen auf Ordinalebene gemessen werden, müssen Sie den Spearman-Korrelationskoeffizienten zwischen ihnen berechnen.

Verwandte Themen: Messebenen: Nominal, Ordinal, Intervall und Verhältnis

Hypothese 2: Lineare Beziehung

Um einen Pearson-Korrelationskoeffizienten zwischen zwei Variablen zu berechnen, muss zwischen den beiden Variablen eine lineare Beziehung bestehen.

Der einfachste Weg, diese Hypothese zu testen, besteht darin, einfach ein Streudiagramm der beiden Variablen zu erstellen. Wenn die Punkte im Diagramm annähernd einer geraden Linie folgen, besteht ein linearer Zusammenhang:

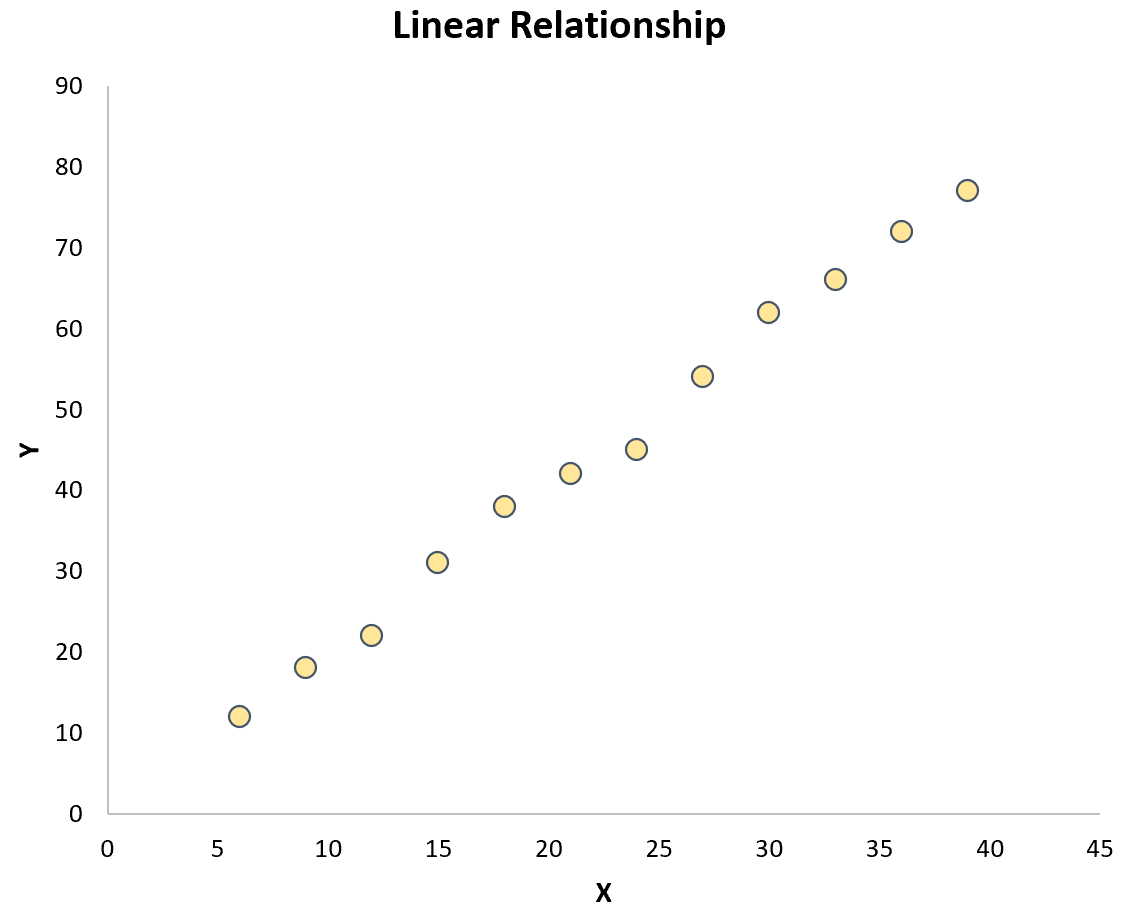
Wenn die Punkte jedoch zufällig über das Diagramm verteilt sind oder eine andere Art von Beziehung (z. B. quadratisch) aufweisen, besteht keine lineare Beziehung zwischen den Variablen:

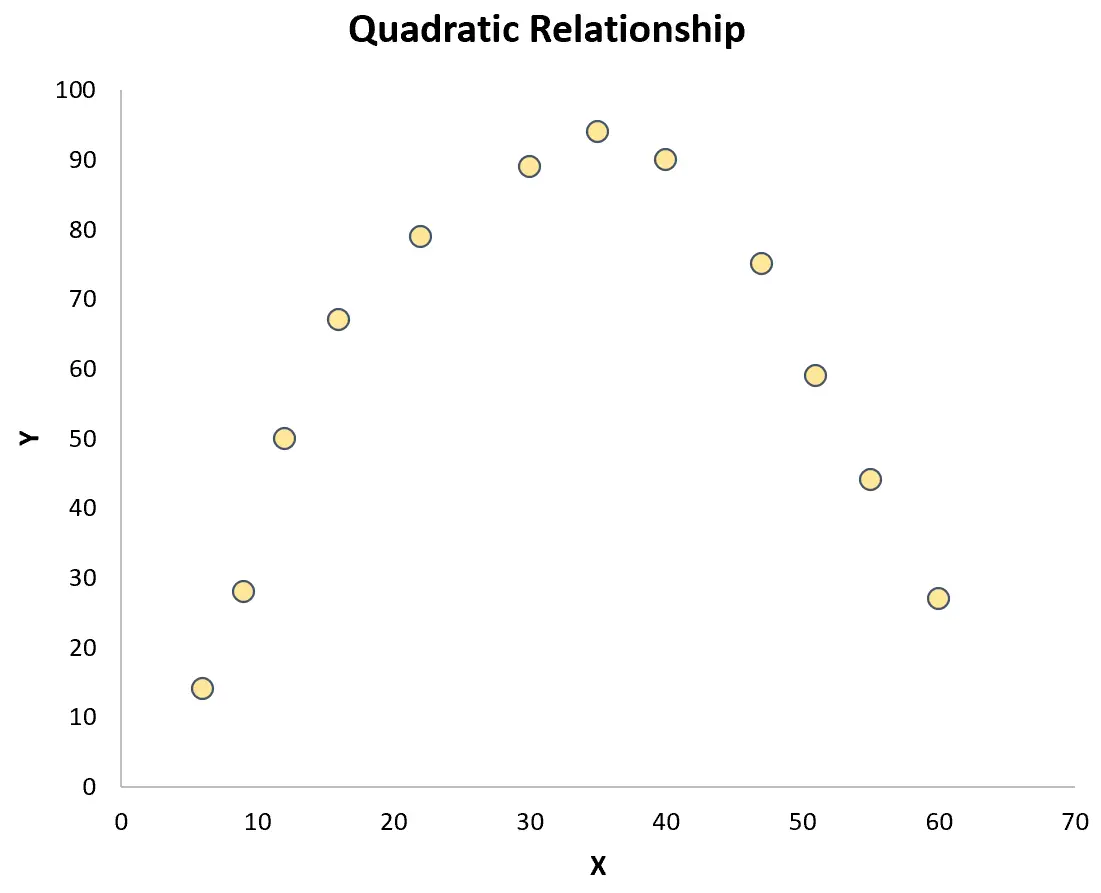
In diesem Fall wird ein Pearson-Korrelationskoeffizient die Beziehung zwischen den Variablen nicht ausreichend erfassen.

Hypothese 3: Normalität

Ein Pearson-Korrelationskoeffizient geht außerdem davon aus, dass die beiden Variablen annähernd normalverteilt sind.

Sie können diese Annahme visuell überprüfen, indem Sie für jede Variable ein Histogramm oder einen QQ-Plot erstellen.

1. Histogramm

Wenn das Histogramm eines Datensatzes ungefähr glockenförmig ist, sind die Daten wahrscheinlich normalverteilt.

2. QQLand

Ein QQ-Diagramm, kurz für „Quantil-Quantil“, ist eine Art Diagramm, das theoretische Quantile entlang der x-Achse (d. h. wo sich Ihre Daten befinden würden, wenn sie einer Normalverteilung folgen würden) und Quantile von Stichproben entlang der y-Achse anzeigt. (d. h. wo sich Ihre Daten tatsächlich befinden).

Wenn die Datenwerte einer annähernd geraden Linie folgen, die einen Winkel von 45 Grad bildet, wird davon ausgegangen, dass die Daten normalverteilt sind.

Sie können auch einen formalen statistischen Test durchführen, um festzustellen, ob eine Variable normalverteilt ist.

Wenn der p-Wert des Tests unter einem bestimmten Signifikanzniveau liegt (z. B. α = 0,05), verfügen Sie über ausreichende Beweise dafür, dass die Daten nicht normalverteilt sind.

Es gibt drei statistische Tests, die üblicherweise zum Testen der Normalität verwendet werden:

1. Der Jarque-Bera-Test

• So führen Sie einen Jarque-Bera-Test in Excel durch
• So führen Sie einen Jarque-Bera-Test in R durch
• So führen Sie einen Jarque-Bera-Test in Python durch

2. Der Shapiro-Wilk-Test

• So führen Sie einen Shapiro-Wilk-Test in R durch
• So führen Sie einen Shapiro-Wilk-Test in Python durch

3. Der Kolmogorov-Smirnov-Test

• So führen Sie einen Kolmogorov-Smirnov-Test in R durch
• So führen Sie einen Kolmogorov-Smirnov-Test in Python durch

Hypothese 4: Verwandte Paare

Ein Pearson-Korrelationskoeffizient geht außerdem davon aus, dass jede Beobachtung im Datensatz ein Wertepaar haben muss.

Diese Hypothese ist leicht zu überprüfen. Wenn Sie beispielsweise die Korrelation zwischen Gewicht und Größe berechnen, stellen Sie einfach sicher, dass jede Beobachtung im Datensatz über ein Maß für Gewicht und ein Maß für Größe verfügt.

Hypothese 5: Keine Ausreißer

Bei einem Pearson-Korrelationskoeffizienten wird außerdem davon ausgegangen, dass der Datensatz keine extremen Ausreißer enthält, da Ausreißer die Berechnung des Korrelationskoeffizienten stark beeinflussen.

Betrachten Sie zur Veranschaulichung den folgenden Datensatz:

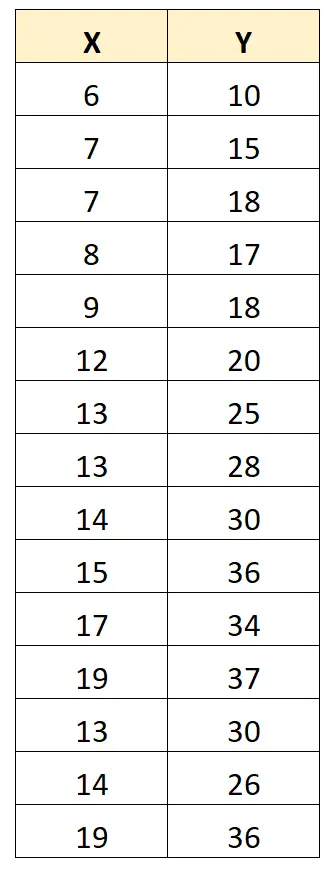
Der Pearson-Korrelationskoeffizient zwischen X und Y beträgt 0,949 .

Nehmen wir jedoch an, wir haben einen Ausreißer im Datensatz:

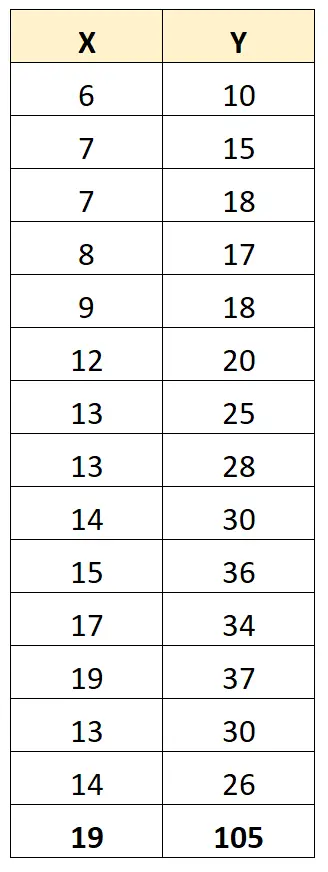
Der Pearson-Korrelationskoeffizient zwischen X und Y beträgt jetzt 0,711 .

Ein Ausreißer verändert den Pearson-Korrelationskoeffizienten zwischen den beiden Variablen erheblich. In diesem Fall kann es sinnvoll sein, den Ausreißer aus dem Datensatz zu entfernen.

Verwandte Themen: Der vollständige Leitfaden: Wann Ausreißer in Daten entfernt werden sollten

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zur Pearson-Korrelation:

Einführung in den Pearson-Korrelationskoeffizienten
So melden Sie die Pearson-Korrelation im APA-Format
So berechnen Sie manuell einen Pearson-Korrelationskoeffizienten