Pearson-korrelationskoeffizient

Der Pearson-Korrelationskoeffizient (auch als „Produkt-Moment-Korrelationskoeffizient“ bekannt) ist ein Maß für den linearen Zusammenhang zwischen zwei Variablen X und Y. Er hat einen Wert zwischen -1 und 1, wobei:

• -1 zeigt eine vollkommen negative lineare Korrelation zwischen zwei Variablen an
• 0 bedeutet, dass zwischen zwei Variablen keine lineare Korrelation besteht
• 1 zeigt eine vollkommen positive lineare Korrelation zwischen zwei Variablen an

Die Formel zur Ermittlung des Pearson-Korrelationskoeffizienten

Die Formel zum Ermitteln des Pearson-Korrelationskoeffizienten, bezeichnet mit r , für eine Datenstichprobe lautet ( über Wikipedia ):

Wahrscheinlich müssen Sie diese Formel nie von Hand berechnen, da Sie dies mithilfe einer Software erledigen können. Es ist jedoch hilfreich, anhand eines Beispiels zu verstehen, was diese Formel genau bewirkt.

Angenommen, wir haben den folgenden Datensatz:

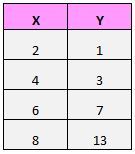
Wenn wir diese Paare (X, Y) in einem Streudiagramm darstellen, würde es so aussehen:

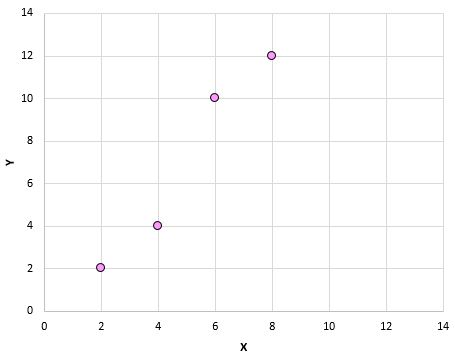
Wenn wir uns dieses Streudiagramm ansehen, können wir erkennen, dass zwischen den Variablen X und Y ein positiver Zusammenhang besteht: Wenn X zunimmt, nimmt auch Y tendenziell zu. Um jedoch genau zu quantifizieren, wie positiv diese beiden Variablen miteinander verbunden sind, müssen wir den Pearson-Korrelationskoeffizienten ermitteln.

Konzentrieren wir uns einfach auf den Zähler der Formel:

Für jedes Paar (X, Y) in unserem Datensatz müssen wir die Differenz zwischen dem x-Wert und dem durchschnittlichen x-Wert sowie die Differenz zwischen dem y-Wert und dem durchschnittlichen y-Wert ermitteln und diese beiden Zahlen dann miteinander multiplizieren.

Zum Beispiel ist unser erstes Paar (X, Y) (2, 2). Der Durchschnittswert von x in diesem Datensatz beträgt 5 und der Durchschnittswert von y in diesem Datensatz beträgt 7. Die Differenz zwischen dem x-Wert dieses Paares und dem Durchschnittswert von x beträgt also 2 – 5 = -3. Die Differenz zwischen dem y-Wert dieses Paares und dem durchschnittlichen y-Wert beträgt 2 – 7 = -5. Wenn wir dann diese beiden Zahlen multiplizieren, erhalten wir -3 * -5 = 15.

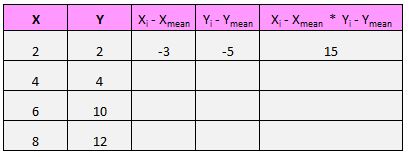
Hier ist ein visueller Überblick über das, was wir gerade gemacht haben:

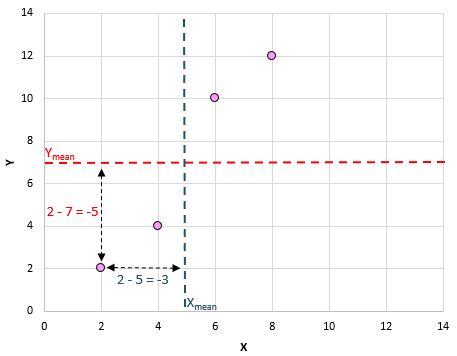
Dann machen Sie einfach für jedes Paar Folgendes:

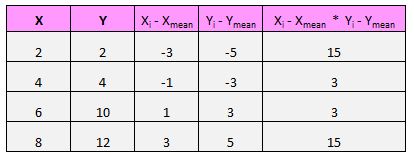
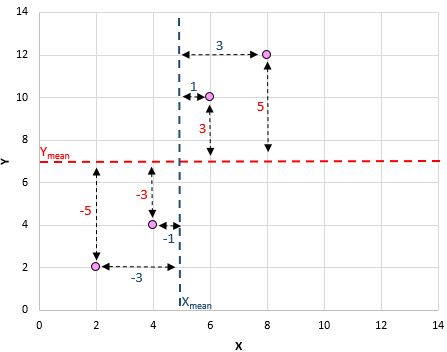
Der letzte Schritt, um den Zähler der Formel zu erhalten, besteht darin, einfach alle diese Werte zu addieren:

15 + 3 +3 + 15 = 36

Dann sagt uns der Nenner der Formel, dass wir die Summe aller quadrierten Differenzen für x und y ermitteln, dann diese beiden Zahlen miteinander multiplizieren und dann die Quadratwurzel ziehen sollen:

Zuerst ermitteln wir die Summe der Quadrate der Differenzen für x und y:

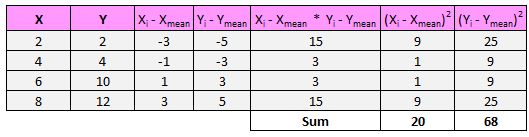
Als nächstes multiplizieren wir diese beiden Zahlen miteinander: 20 * 68 = 1.360.

Zum Schluss ziehen wir die Quadratwurzel: √ 1.360 = 36,88

Wir haben also herausgefunden, dass der Zähler der Formel 36 und der Nenner 36,88 ist. Das bedeutet, dass unser Pearson-Korrelationskoeffizient r = 36 / 36,88 = 0,976 beträgt

Diese Zahl liegt nahe bei 1, was darauf hinweist, dass zwischen unseren Variablen X und Y eine starke positive lineare Beziehung besteht. Dies bestätigt die Beziehung, die wir im Streudiagramm beobachtet haben.

Korrelationen anzeigen

Denken Sie daran, dass ein Pearson-Korrelationskoeffizient uns die Art der linearen Beziehung (positiv, negativ, keine) zwischen zwei Variablen sowie die Stärke dieser Beziehung (schwach, mäßig, stark) angibt.

Wenn wir ein Streudiagramm zweier Variablen erstellen, können wir die tatsächliche Beziehung zwischen zwei Variablen erkennen . Hier sind die vielen Arten linearer Beziehungen, die wir beobachten könnten:

Starke, positive Beziehung: Wenn die Variable auf der x-Achse zunimmt, nimmt auch die Variable auf der y-Achse zu. Die Punkte liegen eng beieinander, was auf eine starke Beziehung hindeutet.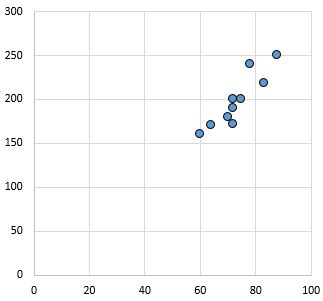

Pearson-Korrelationskoeffizient: 0,94

Schwache und positive Beziehung: Wenn die Variable auf der x-Achse zunimmt, nimmt auch die Variable auf der y-Achse zu. Die Punkte sind ziemlich verstreut, was auf eine schwache Beziehung hindeutet.

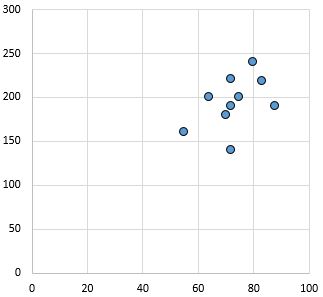
Pearson-Korrelationskoeffizient: 0,44

Keine Beziehung: Es besteht keine eindeutige Beziehung (positiv oder negativ) zwischen den Variablen.

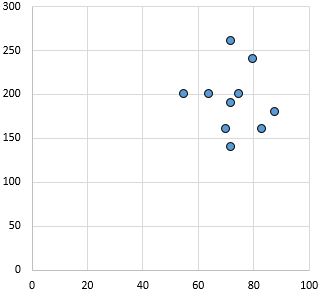
Pearson-Korrelationskoeffizient: 0,03

Starker, negativer Zusammenhang: Wenn die Variable auf der x-Achse zunimmt, nimmt die Variable auf der y-Achse ab. Die Punkte liegen dicht beieinander, was auf eine starke Beziehung hindeutet.

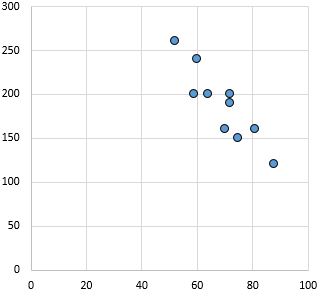
Pearson-Korrelationskoeffizient: -0,87

Schwache und negative Beziehung: Wenn die Variable auf der x-Achse zunimmt, nimmt die Variable auf der y-Achse ab. Die Punkte sind ziemlich verstreut, was auf eine schwache Beziehung hindeutet.

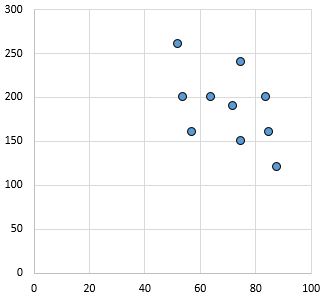
Pearson-Korrelationskoeffizient: – 0,46

Testen der Signifikanz eines Pearson-Korrelationskoeffizienten

Wenn wir den Pearson-Korrelationskoeffizienten für einen Datensatz ermitteln, arbeiten wir häufig mit einer Datenstichprobe aus einer größeren Population . Dies bedeutet, dass es möglich ist, für zwei Variablen eine Korrelation ungleich Null zu finden, selbst wenn sie in der Gesamtpopulation tatsächlich unkorreliert sind.

Angenommen, wir erstellen ein Streudiagramm für die Variablen X und Y für jeden Datenpunkt in der gesamten Grundgesamtheit und es sieht so aus:

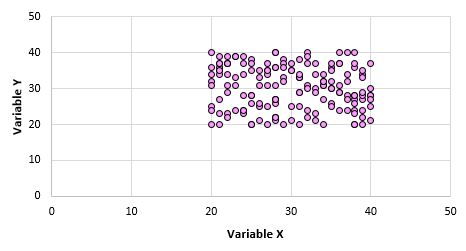
Es ist offensichtlich, dass diese beiden Variablen nicht korrelieren. Es ist jedoch möglich, dass wir, wenn wir eine Stichprobe von 10 Punkten aus der Grundgesamtheit ziehen, die folgenden Punkte auswählen:

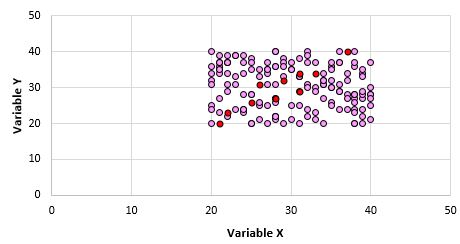
Wir können sehen, dass der Pearson-Korrelationskoeffizient für diese Stichprobe 0,93 beträgt, was auf eine starke positive Korrelation hinweist, obwohl die Populationskorrelation Null ist.

Um zu testen, ob eine Korrelation zwischen zwei Variablen statistisch signifikant ist oder nicht, können wir die folgende Teststatistik finden:

Teststatistik T = r * √ (n-2) / (1-r ² )

Dabei ist n die Anzahl der Paare in unserer Stichprobe, r der Pearson-Korrelationskoeffizient und die T-Teststatistik folgt einer Verteilung mit n-2 Freiheitsgraden.

Sehen wir uns ein Beispiel an, wie die Signifikanz eines Pearson-Korrelationskoeffizienten getestet wird.

Beispiel

Der folgende Datensatz zeigt die Größe und das Gewicht von 12 Personen:

Das Streudiagramm unten zeigt den Wert dieser beiden Variablen:

Der Pearson-Korrelationskoeffizient für diese beiden Variablen beträgt r = 0,836.

Die Teststatistik T = 0,836 * √ (12 -2) / (1-0,836 ² ) = 4,804.

Laut unserem t-Verteilungsrechner hat ein Wert von 4,804 mit 10 Freiheitsgraden einen p-Wert von 0,0007. Da 0,0007 < 0,05 ist, können wir daraus schließen, dass die Korrelation zwischen Gewicht und Größe in diesem Beispiel bei Alpha = 0,05 statistisch signifikant ist.

Vorsichtsmaßnahmen

Obwohl ein Pearson-Korrelationskoeffizient hilfreich sein kann, um uns zu sagen, ob zwei Variablen einen linearen Zusammenhang haben oder nicht, müssen wir bei der Interpretation eines Pearson-Korrelationskoeffizienten drei Dinge im Hinterkopf behalten:

1. Korrelation bedeutet keine Kausalität. Es liegt nicht daran, dass zwei Variablen korrelieren, sodass die eine zwangsläufig dazu führt , dass die andere häufiger oder seltener auftritt. Ein klassisches Beispiel hierfür ist der positive Zusammenhang zwischen Eisverkäufen und Hai-Angriffen. Wenn der Eisverkauf zu bestimmten Zeiten im Jahr steigt, kommt es tendenziell auch zu einer Zunahme von Hai-Angriffen.

Bedeutet das, dass der Verzehr von Eis zu Hai-Angriffen führt ? Natürlich nicht! Das bedeutet einfach, dass im Sommer der Eisverbrauch und die Hai-Angriffe tendenziell zunehmen, weil Eis im Sommer beliebter ist und im Sommer mehr Menschen ins Meer gehen.

2. Korrelationen reagieren empfindlich auf Ausreißer. Ein extremer Ausreißer kann einen Pearson-Korrelationskoeffizienten erheblich verändern. Betrachten Sie das folgende Beispiel:

Die Variablen X und Y haben einen Pearson-Korrelationskoeffizienten von 0,00 . Aber stellen Sie sich vor, wir hätten einen Ausreißer im Datensatz:

Der Pearson-Korrelationskoeffizient für diese beiden Variablen beträgt jedoch 0,878 . Dieser eine Ausreißer verändert alles. Aus diesem Grund ist es bei der Berechnung der Korrelation für zwei Variablen sinnvoll, die Variablen mithilfe eines Streudiagramms zu visualisieren, um auf Ausreißer zu prüfen.

3. Ein Pearson-Korrelationskoeffizient erfasst keine nichtlinearen Beziehungen zwischen zwei Variablen. Stellen wir uns vor, wir haben zwei Variablen mit der folgenden Beziehung:

Der Pearson-Korrelationskoeffizient für diese beiden Variablen beträgt 0,00, da keine lineare Beziehung zwischen ihnen besteht. Allerdings besteht zwischen diesen beiden Variablen ein nichtlinearer Zusammenhang: Die y-Werte sind einfach die x-Werte im Quadrat.

Bedenken Sie bei der Verwendung des Pearson-Korrelationskoeffizienten, dass Sie lediglich testen, ob zwei Variablen linear miteinander verbunden sind. Selbst wenn uns ein Pearson-Korrelationskoeffizient sagt, dass zwei Variablen nicht korreliert sind, könnte zwischen ihnen dennoch eine Art nichtlineare Beziehung bestehen. Dies ist ein weiterer Grund, warum es nützlich ist, bei der Analyse der Beziehung zwischen zwei Variablen ein Streudiagramm zu erstellen: Es kann Ihnen dabei helfen, eine nichtlineare Beziehung zu erkennen.