Pearson-korrelationskoeffizient
In diesem Artikel wird erläutert, was der Pearson-Korrelationskoeffizient (oder lineare Korrelationskoeffizient) ist und wofür er verwendet wird. In einer Schritt-für-Schritt-Übung erfahren Sie, wie Sie den Pearson-Korrelationskoeffizienten berechnen. Darüber hinaus können Sie den Wert des Pearson-Korrelationskoeffizienten für jeden Datensatz mit dem Online-Rechner am Ende ermitteln.
Was ist der Korrelationskoeffizient nach Pearson?
Der Pearson-Korrelationskoeffizient , auch linearer Korrelationskoeffizient oder einfach Korrelationskoeffizient genannt, ist ein statistisches Maß, das die Beziehung zwischen zwei Variablen angibt.
Um den Pearson-Korrelationskoeffizienten zwischen zwei Variablen zu berechnen, müssen Sie die Kovarianz dieser Variablen durch die Quadratwurzel des Produkts ihrer Varianzen dividieren.
Somit versucht der Pearson-Korrelationskoeffizient die lineare Abhängigkeit zwischen zwei quantitativen Zufallsvariablen zu quantifizieren. A priori ist es schwierig, die Korrelation zwischen Variablen numerisch auszuwerten, da es schwierig ist, festzustellen, ob das Variablenpaar stärker korreliert ist, wenn, wie in Pues, das Ziel des Pearson-Korrelationskoeffizienten darin besteht, die Beziehung zwischen Variablen bewerten zu können Vergleichen Sie sie.
Der Wert des Pearson-Korrelationsindex liegt zwischen -1 und +1 (einschließlich). Im Folgenden werden wir sehen, wie der Wert des Pearson-Korrelationskoeffizienten interpretiert wird.
Pearson-Korrelationskoeffizientenformel
Der Pearson-Korrelationskoeffizient zweier statistischer Variablen ist gleich dem Quotienten zwischen der Kovarianz der Variablen und der Quadratwurzel des Produkts der Varianz jeder Variablen.
Daher lautet die Formel zur Berechnung des Pearson-Korrelationskoeffizienten wie folgt:
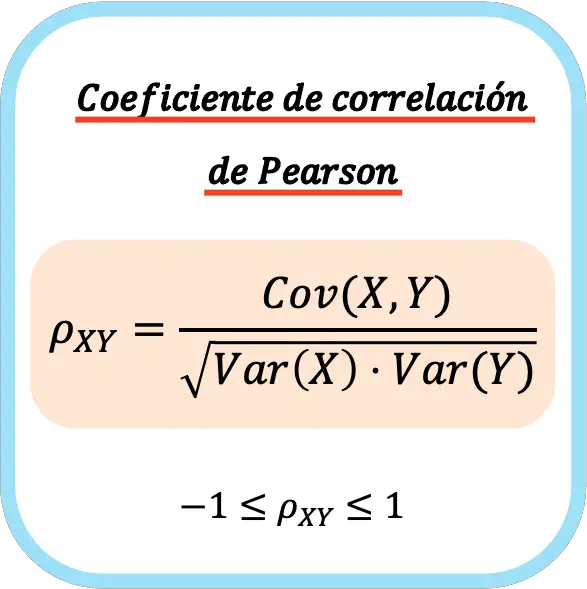
👉 Mit dem Rechner unten können Sie den Pearson-Korrelationskoeffizienten für jeden Datensatz berechnen.
Wenn der Pearson-Korrelationskoeffizient für eine Population berechnet wird, wird er im Allgemeinen durch den griechischen Buchstaben ρ ausgedrückt. Wenn der Koeffizient jedoch relativ zu einer Stichprobe berechnet wird, wird normalerweise der Buchstabe r als Symbol verwendet.
Beachten Sie, dass Sie zur Bestimmung des Pearson-Korrelationskoeffizienten unbedingt wissen müssen, wie die Kovarianz zwischen zwei Variablen und die Varianz einer Variablen berechnet werden. Darüber hinaus müssen Sie verstehen, was diese statistischen Maße bedeuten. Bevor Sie mit der Erklärung fortfahren, wird daher empfohlen, die folgenden beiden Artikel zu lesen:
Beispiel für die Berechnung des Pearson-Korrelationskoeffizienten
Nachfolgend finden Sie ein Schritt-für-Schritt-Beispiel zur Definition des Pearson-Korrelationskoeffizienten und seiner Formel, damit Sie sehen können, wie er berechnet wird.
- Berechnen Sie den Pearson-Korrelationskoeffizienten zwischen den folgenden zwei kontinuierlichen Variablen:

Bevor wir den Pearson-Korrelationskoeffizienten berechnen, stellen wir den Datensatz in einem Streudiagramm dar, um die Beziehung zwischen den beiden Variablen zu analysieren:
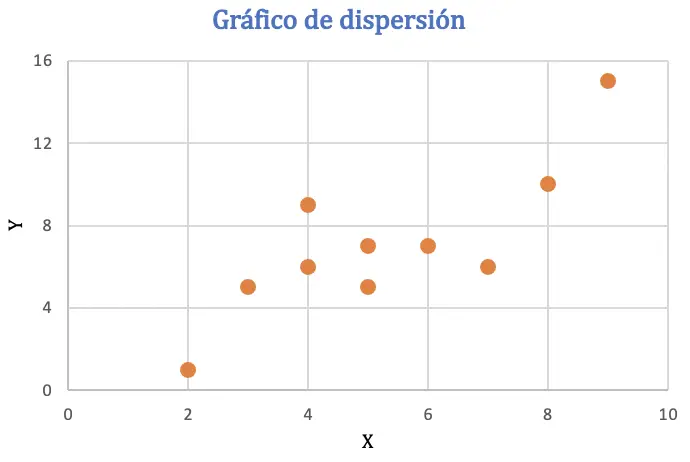
Aus dem Streudiagramm lässt sich ableiten, dass die Daten möglicherweise einen positiven Trend aufweisen. Mit anderen Worten: Wenn der Wert einer Variablen zunimmt, nimmt auch die andere Variable zu. Um die Korrelation zu überprüfen, ermitteln wir den Pearson-Koeffizienten.
Als erstes müssen Sie das arithmetische Mittel jeder Variablen separat ermitteln, was der Gesamtsumme der Daten dividiert durch die Anzahl der Beobachtungen entspricht.
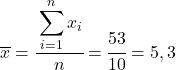
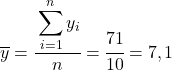
Da wir nun den Mittelwert jeder Variablen kennen, müssen wir der Datentabelle die folgenden Spalten hinzufügen:
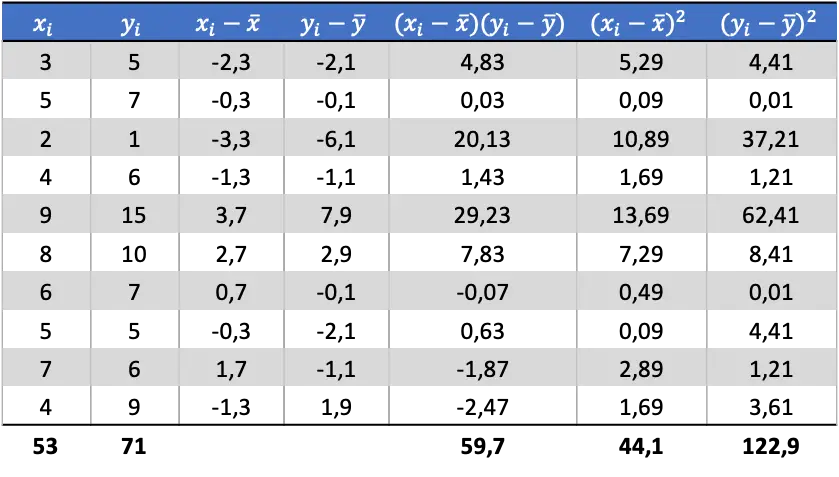
Aus den berechneten Daten in der Tabelle ermitteln wir die Werte der Kovarianz und Varianzen (falls Sie sich nicht erinnern, wie das gemacht wurde, finden Sie oben zwei Links, wo dies im Detail erklärt wird):
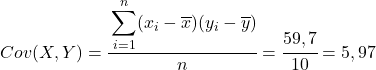
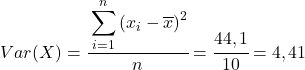
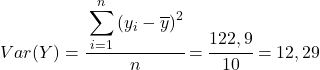
Wenden Sie abschließend einfach die Pearson-Korrelationskoeffizientenformel an, um den Wert zu erhalten:
![]()
Der Pearson-Korrelationskoeffizient hat einen Wert sehr nahe bei 1, was bedeutet, dass diese beiden Variablen eine ziemlich starke positive Korrelation aufweisen.
Wie Sie gesehen haben, ist es zur Bestimmung des Pearson-Korrelationskoeffizienten sehr nützlich, Programme wie Excel zu verwenden, um Spaltenberechnungen schneller durchzuführen.
Pearson-Korrelationskoeffizientenrechner
Geben Sie einen Satz statistischer Daten in den folgenden Rechner ein, um den Pearson-Korrelationskoeffizienten zwischen zwei Variablen zu berechnen. Sie müssen die Datenpaare trennen, sodass im ersten Feld nur die Werte einer Variablen und im zweiten Feld nur die Werte der zweiten Variablen stehen.
Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.
Interpretation des Pearson-Korrelationskoeffizienten
In diesem Abschnitt werden wir sehen, wie der Pearson-Korrelationskoeffizient zu interpretieren ist, denn es reicht nicht aus, seinen Wert zu kennen, sondern man muss wissen, wie man seine Bedeutung analysiert.
Somit hängt die Interpretation des Pearson-Korrelationskoeffizienten von seinem Wert ab:
- r=-1 : Die beiden Variablen weisen eine perfekte negative Korrelation auf, sodass wir eine Linie mit negativer Steigung zeichnen können, in der alle Punkte miteinander verbunden sind.
- -1<r<0 : Die Korrelation zwischen den beiden Variablen ist negativ. Wenn also eine Variable zunimmt, nimmt die andere ab. Je näher der Wert bei -1 liegt, desto negativer sind die Variablen miteinander verknüpft.
- r=0 : Die Korrelation zwischen den beiden Variablen ist sehr schwach, tatsächlich ist die lineare Beziehung zwischen ihnen Null. Dies bedeutet nicht, dass die Variablen unabhängig sind, da sie möglicherweise in einem nichtlinearen Zusammenhang stehen.
- 0<r<1 : Die Korrelation zwischen den beiden Variablen ist positiv. Je näher der Wert an +1 liegt, desto stärker ist die Beziehung zwischen den Variablen. In diesem Fall nimmt der Wert einer Variablen tendenziell zu, wenn auch die andere zunimmt.
- r=1 : Die beiden Variablen haben eine perfekte positive Korrelation, das heißt, sie haben eine positive lineare Beziehung.
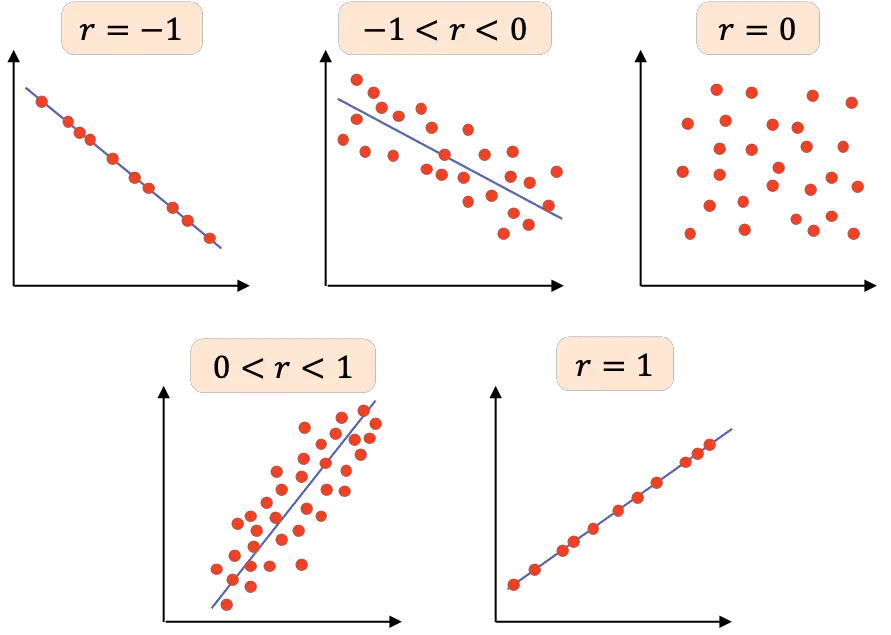
Zusammenfassend wird die folgende Tabelle mit den unterschiedlichen Interpretationen des Pearson-Korrelationskoeffizienten dargestellt:
| Wert | Deutung |
|---|---|
| r=-1 | Perfekte negative Korrelation. |
| -1<r<0 | Negative Korrelation: Je näher die Korrelation bei -1 liegt, desto stärker ist sie. |
| r=0 | Keine lineare Korrelation. |
| 0<r<1 | Positive Korrelation: Je näher die Korrelation bei +1 liegt, desto stärker ist sie. |
| r=1 | Perfekte positive Korrelation. |
Bedenken Sie, dass selbst wenn eine Beziehung zwischen zwei Variablen besteht, dies nicht bedeutet, dass zwischen ihnen eine Kausalität besteht, d. h. die Korrelation zwischen zwei Variablen bedeutet nicht, dass die Änderung einer Variablen die Ursache für die Änderung der Variablen ist. andere Variable.
Wenn wir beispielsweise feststellen, dass ein positiver Zusammenhang zwischen der Produktion zweier verschiedener Hormone im Körper besteht, ist es nicht notwendig, dass ein Anstieg des einen Hormons zu einem Anstieg des anderen Hormons führt. Es könnte sein, dass der Körper beide Hormone produziert, weil er beide zur Bekämpfung einer Krankheit benötigt und daher die Spiegel beider gleichzeitig erhöht. In diesem Fall wäre die Krankheit die Ursache. Um festzustellen, ob ein kausaler Zusammenhang zwischen den beiden Hormonen besteht, sollten weitere Untersuchungen durchgeführt werden.