Was ist perfekte multikollinearität? (definition & beispiele)

In der Statistik liegt Multikollinearität vor, wenn zwei oder mehr Prädiktorvariablen stark miteinander korrelieren, sodass sie im Regressionsmodell keine eindeutigen oder unabhängigen Informationen liefern.

Wenn der Korrelationsgrad zwischen den Variablen hoch genug ist, kann dies zu Problemen bei der Anpassung und Interpretation des Regressionsmodells führen.

Der extremste Fall der Multikollinearität wird als perfekte Multikollinearität bezeichnet. Dies geschieht, wenn zwei oder mehr Prädiktorvariablen eine exakte lineare Beziehung zueinander haben.

Angenommen, wir haben den folgenden Datensatz:

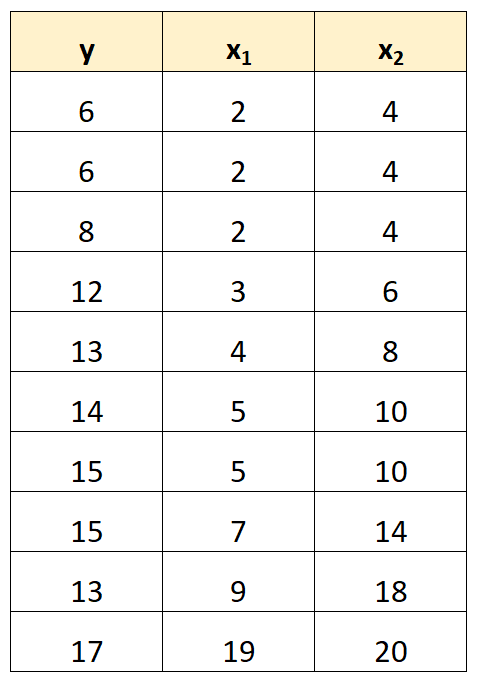
Beachten Sie, dass die Werte der Prädiktorvariablen x ₂ einfach die Werte von x ₁ multipliziert mit 2 sind.

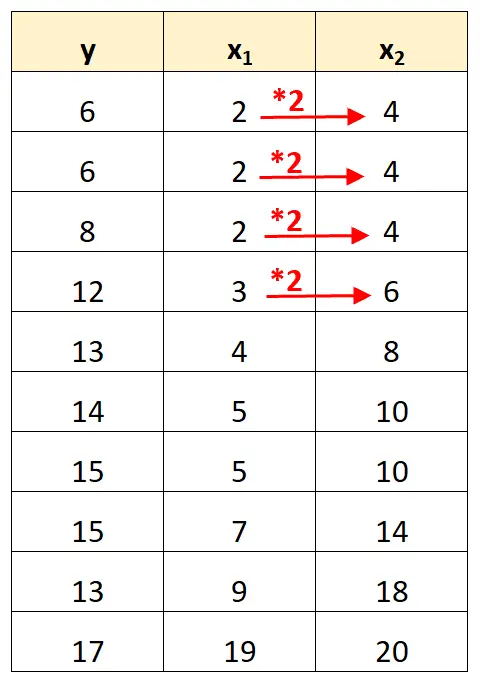
Dies ist ein Beispiel für perfekte Multikollinearität .

Das Problem der perfekten Multikollinearität

Wenn in einem Datensatz perfekte Multikollinearität vorhanden ist, können mithilfe der Methode der kleinsten Quadrate keine Schätzungen der Regressionskoeffizienten erstellt werden.

Tatsächlich ist es nicht möglich, den marginalen Effekt einer Prädiktorvariablen (x ₁ ) auf die Antwortvariable (y) abzuschätzen und gleichzeitig eine andere Prädiktorvariable (x ₂ ) konstant zu halten, da sich x ₂ immer genau bewegt, wenn sich x ₁ bewegt.

Kurz gesagt, perfekte Multikollinearität macht es unmöglich, für jeden Koeffizienten in einem Regressionsmodell einen Wert zu schätzen.

Wie man mit perfekter Multikollinearität umgeht

Der einfachste Weg, mit perfekter Multikollinearität umzugehen, besteht darin, eine der Variablen zu entfernen, die eine exakte lineare Beziehung zu einer anderen Variablen aufweist.

In unserem vorherigen Datensatz könnten wir beispielsweise einfach x ₂ als Prädiktorvariable entfernen.

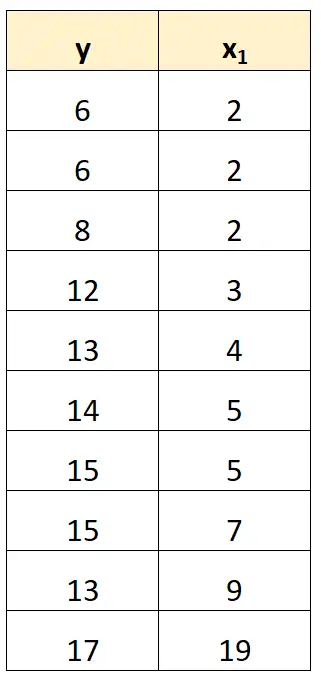
Anschließend würden wir ein Regressionsmodell mit x ₁ als Prädiktorvariable und y als Antwortvariable anpassen.

Beispiele perfekter Multikollinearität

Die folgenden Beispiele zeigen die drei häufigsten Szenarien perfekter Multikollinearität in der Praxis.

1. Eine Prädiktorvariable ist ein Vielfaches einer anderen

Nehmen wir an, wir möchten „Größe in Zentimetern“ und „Größe in Metern“ verwenden, um das Gewicht einer bestimmten Delfinart vorherzusagen.

So könnte unser Datensatz aussehen:

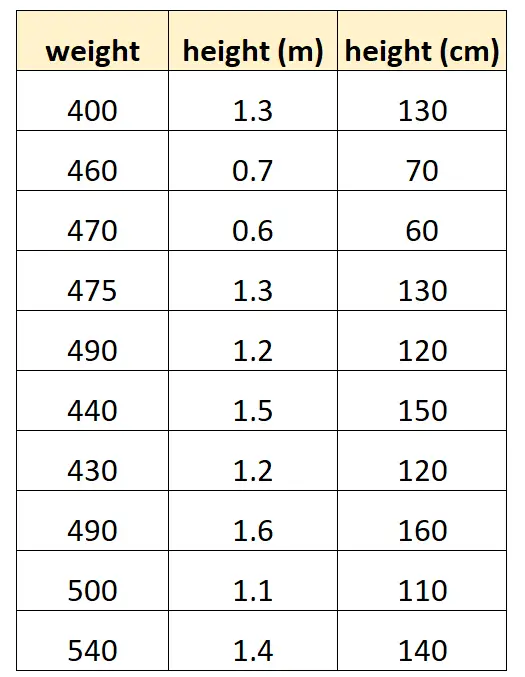
Beachten Sie, dass der Wert „Höhe in Zentimetern“ einfach gleich „Höhe in Metern“ multipliziert mit 100 ist. Dies ist ein Fall perfekter Multikollinearität.

Wenn wir versuchen, mithilfe dieses Datensatzes ein multiples lineares Regressionsmodell in R anzupassen, können wir keine Koeffizientenschätzung für die Prädiktorvariable „Meter“ erstellen:

 #define data
df <- data. frame (weight=c(400, 460, 470, 475, 490, 440, 430, 490, 500, 540),
                 m=c(1.3, .7, .6, 1.3, 1.2, 1.5, 1.2, 1.6, 1.1, 1.4),
                 cm=c(130, 70, 60, 130, 120, 150, 120, 160, 110, 140))

#fit multiple linear regression model
model <- lm(weight~m+cm, data=df)

#view summary of model
summary(model)

Call:
lm(formula = weight ~ m + cm, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-70,501 -25,501 5,183 19,499 68,590 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 458,676 53,403 8,589 2.61e-05 ***
m 9.096 43.473 0.209 0.839    
cm NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 41.9 on 8 degrees of freedom
Multiple R-squared: 0.005442, Adjusted R-squared: -0.1189 
F-statistic: 0.04378 on 1 and 8 DF, p-value: 0.8395

2. Eine Prädiktorvariable ist eine transformierte Version einer anderen

Nehmen wir an, wir möchten „Punkte“ und „skalierte Punkte“ verwenden, um die Bewertung von Basketballspielern vorherzusagen.

Angenommen, die Variable „skalierte Punkte“ wird wie folgt berechnet:

Skalierte Punkte = (Punkte – μ- _Punkte ) / σ- _Punkte

So könnte unser Datensatz aussehen:

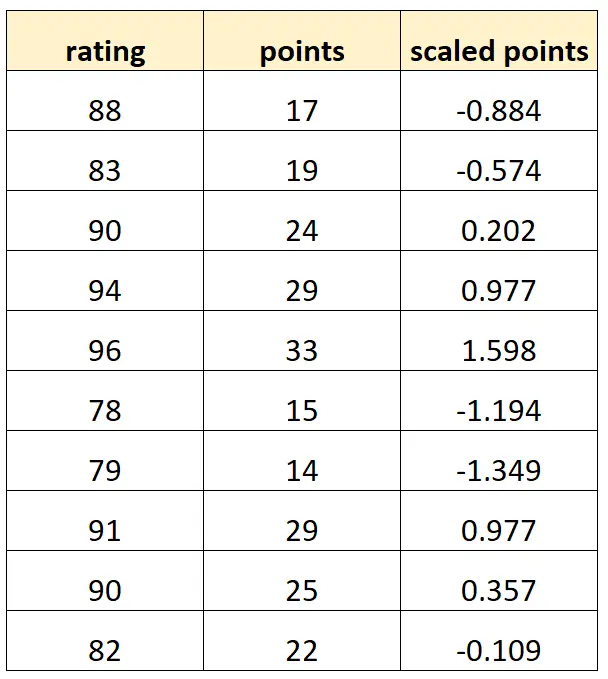
Beachten Sie, dass jeder „skalierte Punkte“-Wert lediglich eine standardisierte Version von „Punkten“ ist. Dies ist ein Fall perfekter Multikollinearität.

Wenn wir versuchen, mithilfe dieses Datensatzes ein multiples lineares Regressionsmodell in R anzupassen, können wir keine Koeffizientenschätzung für die Prädiktorvariable „skalierte Punkte“ erstellen:

 #define data
df <- data. frame (rating=c(88, 83, 90, 94, 96, 78, 79, 91, 90, 82),
                 pts=c(17, 19, 24, 29, 33, 15, 14, 29, 25, 22))

df$scaled_pts <- (df$pts - mean(df$pts)) / sd(df$pts)

#fit multiple linear regression model
model <- lm(rating~pts+scaled_pts, data=df)

#view summary of model
summary(model)

Call:
lm(formula = rating ~ pts + scaled_pts, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4932 -1.3941 -0.2935 1.3055 5.8412 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 67.4218 3.5896 18.783 6.67e-08 ***
pts 0.8669 0.1527 5.678 0.000466 ***
scaled_pts NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.953 on 8 degrees of freedom
Multiple R-squared: 0.8012, Adjusted R-squared: 0.7763 
F-statistic: 32.23 on 1 and 8 DF, p-value: 0.0004663

3. Die Dummy-Variablenfalle

Ein weiteres Szenario, in dem perfekte Multikollinearität auftreten kann, ist als Dummy-Variablenfalle bekannt. Dies ist der Fall, wenn wir eine kategoriale Variable in einem Regressionsmodell nehmen und sie in eine „Dummy-Variable“ umwandeln möchten, die die Werte 0, 1, 2 usw. annimmt.

Nehmen wir zum Beispiel an, wir möchten die Prädiktorvariablen „Alter“ und „Familienstand“ verwenden, um das Einkommen vorherzusagen:

Um „Familienstand“ als Prädiktorvariable zu verwenden, müssen wir ihn zunächst in eine Dummy-Variable umwandeln.

Dazu können wir „Single“ als Basiswert belassen, da dies am häufigsten vorkommt, und „Verheiratet“ und „Geschieden“ wie folgt Werte von 0 oder 1 zuweisen:

Ein Fehler wäre, drei neue Dummy-Variablen wie folgt zu erstellen:

In diesem Fall ist die Variable „Single“ eine perfekte lineare Kombination der Variablen „Verheiratet“ und „Geschieden“. Dies ist ein Beispiel für perfekte Multikollinearität.

Wenn wir versuchen, mithilfe dieses Datensatzes ein multiples lineares Regressionsmodell in R anzupassen, können wir nicht für jede Prädiktorvariable eine Koeffizientenschätzung erstellen:

 #define data
df <- data. frame (income=c(45, 48, 54, 57, 65, 69, 78, 83, 98, 104, 107),
                 age=c(23, 25, 24, 29, 38, 36, 40, 59, 56, 64, 53),
                 single=c(1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0),
                 married=c(0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1),
                 divorced=c(0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0))

#fit multiple linear regression model
model <- lm(income~age+single+married+divorced, data=df)

#view summary of model
summary(model)

Call:
lm(formula = income ~ age + single + married + divorced, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-9.7075 -5.0338 0.0453 3.3904 12.2454 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)   
(Intercept) 16.7559 17.7811 0.942 0.37739   
age 1.4717 0.3544 4.152 0.00428 **
single -2.4797 9.4313 -0.263 0.80018   
married NA NA NA NA   
divorced -8.3974 12.7714 -0.658 0.53187   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 8.391 on 7 degrees of freedom
Multiple R-squared: 0.9008, Adjusted R-squared: 0.8584 
F-statistic: 21.2 on 3 and 7 DF, p-value: 0.0006865

Zusätzliche Ressourcen

Ein Leitfaden zu Multikollinearität und VIF in der Regression
So berechnen Sie VIF in R
So berechnen Sie VIF in Python
So berechnen Sie den VIF in Excel