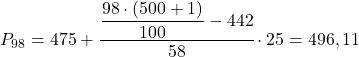Perzentile (statistik)
In diesem Artikel wird erklärt, was ein Perzentil ist und wie es berechnet wird. Sie finden gelöste Perzentilübungen und können darüber hinaus jedes beliebige Perzentil Ihrer Datenstichprobe mit einem Online-Rechner berechnen.
Was sind Perzentile?
In der Statistik sind Perzentile die Werte, die einen Satz geordneter Daten in hundert gleiche Teile teilen. Ein Perzentil gibt also den Wert an, unter den ein Prozentsatz des Datensatzes fällt.
Beispielsweise ist der 35. Perzentilwert höher als 35 % der beobachteten Daten, aber niedriger als der Rest der Daten.
Perzentile werden durch den Großbuchstaben P und den Perzentilindex dargestellt, d. h. das 1. Perzentil ist P 1 , das 40. Perzentil ist P 40 , das 79. Perzentil ist P 79 und so weiter.

👉 Mit dem Rechner unten können Sie Perzentile eines beliebigen Datensatzes berechnen.
In ähnlicher Weise sind Perzentile zusammen mit Quartilen, Quintilen und Dezilen ein Maß für die nicht zentrale Position. Sie können die Bedeutung jedes dieser Quantiltypen auf unserer Website überprüfen.
Zu beachten ist, dass der Begriff Perzentile auch verwendet wird, um das Gewicht und die Größe eines Babys mit den Standardwerten anderer Babys zu vergleichen, da es Wachstumstabellen mit aufgezeichneten Werten gibt, anhand derer festgestellt werden kann, ob das Baby richtig wächst oder nicht. . .
So berechnen Sie Perzentile
Um die Position eines Perzentils einer statistischen Datenreihe zu berechnen , müssen Sie die Perzentilzahl mit der Summe der Gesamtzahl der Datenpunkte plus eins multiplizieren und das Ergebnis durch einhundert dividieren.
Die Perzentilformel lautet daher:
![]()
Bitte beachten Sie: Diese Formel sagt uns die Position des Perzentils, nicht jedoch seinen Wert. Das Perzentil sind die Daten, die sich an der durch die Formel ermittelten Position befinden.
Manchmal liefert uns das Ergebnis dieser Formel jedoch eine Dezimalzahl. Daher müssen wir zwei Fälle unterscheiden, je nachdem, ob das Ergebnis eine Dezimalzahl ist oder nicht:
- Wenn das Ergebnis der Formel eine Zahl ohne Dezimalteil ist, entspricht das Perzentil den Daten, die sich an der in der obigen Formel angegebenen Position befinden.
- Wenn das Formelergebnis eine Zahl mit Dezimalteil ist, wird der genaue Perzentilwert anhand der folgenden Formel berechnet:
![]()
Dabei sind x i und x i+1 die Zahlen der Positionen, zwischen denen sich die durch die erste Formel erhaltene Zahl befindet, und d ist der Dezimalteil der durch die erste Formel erhaltenen Zahl.
Sie denken jetzt vielleicht, dass das Ermitteln der Perzentile einer statistischen Stichprobe oder Population kompliziert ist, weil die Methode viele Schritte erfordert, aber eigentlich ist es einfach. Lesen Sie die folgenden zwei konkreten Beispiele und ich bin sicher, Sie werden es viel besser verstehen.
Hinweis : Die wissenschaftliche Gemeinschaft ist sich noch nicht ganz einig, wie Perzentile berechnet werden, daher gibt es ein Statistikbuch, das dies etwas anders erklärt.
Beispiele für Perzentilberechnungen
Wie Sie oben in der Erklärung zum Ermitteln der Perzentile einer Stichprobe gesehen haben, hängt die Berechnung davon ab, ob das Ergebnis der ersten Formel dezimal ist oder nicht. Deshalb finden Sie unten zwei gelöste Beispiele, eines für jeden Fall.
Beispiel 1
- Berechnen Sie anhand der in der folgenden Tabelle gezeigten Daten das 1., 43. und 89. Perzentil.
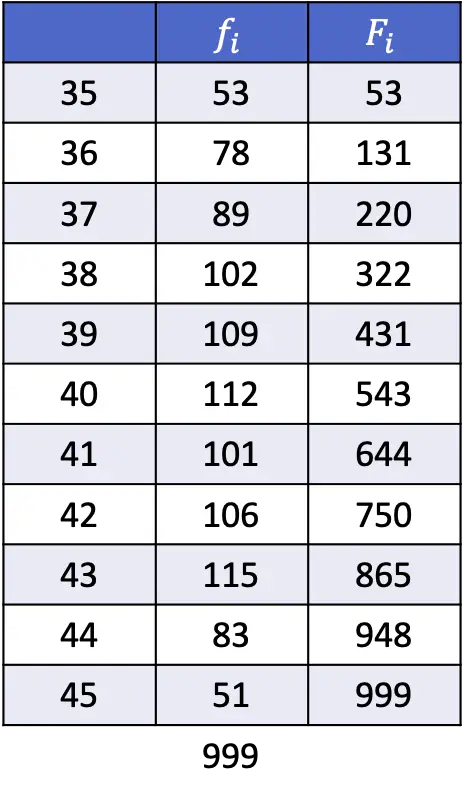
Wie im vorherigen Abschnitt erläutert, lautet die Formel zum Ermitteln der Position eines Perzentils:
![]()
In diesem Fall beträgt die Stichprobengröße für diese Übung 999 statistische Daten. Um die Position des ersten Perzentils zu berechnen, müssen wir n durch 999 und k durch 1 ersetzen:
![]()
Das 1. Perzentil ist also dasjenige, dessen kumulative absolute Häufigkeit unmittelbar größer als 10 ist, was in diesem Fall 35 ist, da es eine kumulative absolute Häufigkeit von 53 hat.
Um das 43. Perzentil zu bestimmen, müssen Sie dieselbe Formel verwenden, aber dieses Mal ersetzen wir natürlich k durch 43.
![]()
Die absolute kumulative Häufigkeit unmittelbar über 430 beträgt 431 der Daten 39, sodass das 43. Perzentil gleich 39 ist.
Schließlich wenden wir dieselbe Formel an, um das 89. Perzentil zu erhalten:
![]()
Die kumulative absolute Häufigkeit des Werts 44 beträgt 948, was unmittelbar größer als 890 ist. Daher beträgt das 89. Perzentil 44.
Beispiel 2
- Finden Sie das 35. und 67. Perzentil der folgenden Datenreihen:
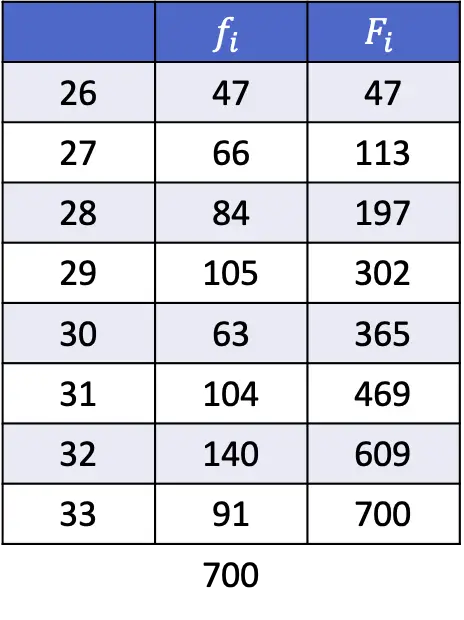
Auch wenn wir in dieser Übung weitere Berechnungen durchführen müssen, ist das Prinzip immer noch dasselbe: Wir müssen die Perzentilposition mit dem folgenden Ausdruck berechnen.
![]()
Um das 35. Perzentil zu berechnen, ersetzen wir also k durch 35 und n durch die Gesamtzahl der Daten, also 700:
![]()
Aber dieses Mal haben wir eine Dezimalzahl aus der Formel erhalten, also müssen wir den folgenden algebraischen Ausdruck anwenden, um den genauen Perzentilwert zu berechnen:
![]()
Die durch die erste Formel angegebene Zahl ist 245,35, das 35. Perzentil liegt also zwischen den Positionen 245 und 246, was den Werten 29 bzw. 29 entspricht. Daher ist x i 29, x i+1 ist 29 und d ist der Dezimalteil der erhaltenen Zahl, also 0,35.
![]()
Um das 67. Perzentil zu finden, müssen wir dieselbe Methode verwenden. Wir berechnen zunächst die Perzentilposition:
![]()
Die resultierende Zahl 469,67 gibt an, dass das Perzentil zwischen den Positionen 469 und 470 liegen wird, deren Werte 31 und 32 sind. Daher verwenden wir dabei die zweite Formel, um den genauen Perzentilwert zu ermitteln:
![]()
Perzentilrechner
Geben Sie einen statistischen Datensatz und die Perzentilzahl, die Sie berechnen möchten, in den folgenden Rechner ein. Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.
Perzentile in gruppierten Daten
Um Perzentile zu berechnen, wenn Daten in Gruppen gruppiert sind , müssen wir zunächst mithilfe der folgenden Formel die Gruppe oder Klasse ermitteln, in die das Perzentil fällt:
![]()
Das Perzentil liegt daher in dem Intervall, dessen absolute Häufigkeit unmittelbar größer ist als die im vorherigen Ausdruck erhaltene Zahl.
Und sobald wir bereits wissen, zu welchem Intervall das Perzentil gehört, müssen wir die folgende Formel anwenden, um den genauen Wert des Perzentils zu ermitteln:
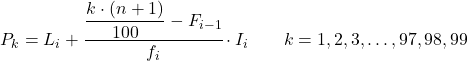
Gold:
- L i ist die untere Grenze des Intervalls, in dem das Perzentil liegt.
- n ist die Gesamtzahl der Beobachtungen.
- F i-1 ist die kumulative absolute Häufigkeit des vorherigen Intervalls.
- f i ist die absolute Häufigkeit des Intervalls, in dem das Perzentil liegt.
- I i ist die Breite des Perzentilintervalls.
Nachfolgend finden Sie eine Schritt-für-Schritt-Übung zum Erhalten von Perzentilen, wenn Daten in Intervallen ausgedrückt werden. Konkret werden das 29., 52. und 98. Perzentil berechnet.

Die Daten in diesem Beispiel sind als Intervalle gruppiert, daher müssen wir zwei Schritte ausführen, um die Perzentile zu bestimmen: Zuerst müssen wir das Intervall ermitteln, in das das Perzentil fällt, und dann die Formel anwenden, um den genauen Wert des Perzentils zu berechnen. Perzentil.
Somit ermitteln wir die Position des 29. Perzentils mit folgendem Ausdruck:
![]()
![]()
Das Perzentilintervall ist dasjenige, dessen kumulative absolute Häufigkeit unmittelbar größer als 145,29 ist, was in diesem Fall das Intervall [350,375) ist, dessen kumulative absolute Häufigkeit 175 beträgt. Und sobald wir das Perzentilintervall kennen, wenden wir die folgende Formel an, um es zu berechnen genauer Wert:
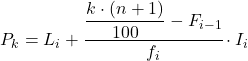
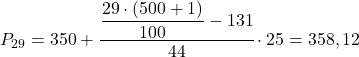
Jetzt wiederholen wir den gleichen Vorgang, um das 52. Perzentil zu berechnen. Wir berechnen zunächst sein Intervall:
![]()
Das 52. Perzentilintervall beträgt [400,425), da seine kumulative absolute Häufigkeit (298) unmittelbar über 260,52 liegt. Der genaue Wert des Perzentils beträgt daher:
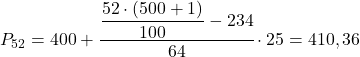
Schließlich finden wir das 98. Perzentil. Wie immer berechnen wir zunächst das Intervall, in dem es liegt:
![]()
Und sobald wir das Intervall kennen, in dem das Perzentil liegt, berechnen wir seinen genauen Wert mit der folgenden Formel: