So berechnen sie einen phi-koeffizienten in r

Ein Phi-Koeffizient (manchmal auch mittlerer quadratischer Kontingenzkoeffizient genannt) ist ein Maß für die Assoziation zwischen zwei binären Variablen.

Für eine 2×2-Tabelle für zwei Zufallsvariablen x und y :

Der Phi-Koeffizient kann wie folgt berechnet werden:

Φ = (AD-BC) / √ (A+B)(C+D)(A+C)(B+D)

Beispiel: Berechnung eines Phi-Koeffizienten in R

Angenommen, wir möchten wissen, ob das Geschlecht mit der Präferenz für eine politische Partei zusammenhängt oder nicht. Wir nehmen also eine einfache Zufallsstichprobe von 25 Wählern und fragen sie nach ihrer Präferenz für eine politische Partei.

Die folgende Tabelle stellt die Ergebnisse der Umfrage dar:

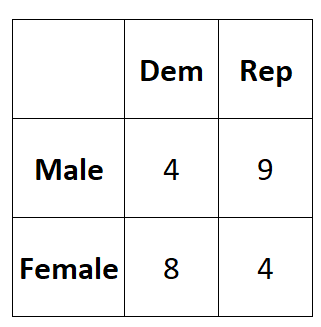
Mit dem folgenden Code können wir diese Daten in eine 2×2-Matrix in R eingeben:

 #create 2x2 table
data = matrix(c(4, 8, 9, 4), nrow = 2 )

#view dataset
data

     [,1] [,2]
[1,] 4 9
[2,] 8 4

Anschließend können wir die Funktion phi() aus dem Paket psych verwenden, um den Phi-Koeffizienten zwischen den beiden Variablen zu berechnen:

 #load psych package
library (psych)

#calculate Phi Coefficient
phi(data)

[1] -0.36

Der Phi-Koeffizient beträgt -0,36 .

Beachten Sie, dass die Phi-Funktion standardmäßig auf zwei Ziffern rundet. Sie können die Funktion jedoch auch so festlegen, dass auf so viele Ziffern gerundet wird, wie Sie möchten:

 #calculate Phi Coefficient and round to 6 digits
phi(data, digits = 6 )

[1] -0.358974

So interpretieren Sie einen Phi-Koeffizienten

Ähnlich wie ein Pearson-Korrelationskoeffizient nimmt ein Phi-Koeffizient Werte zwischen -1 und 1 an, wobei:

• -1 zeigt eine vollkommen negative Beziehung zwischen den beiden Variablen an.
• 0 bedeutet, dass zwischen den beiden Variablen kein Zusammenhang besteht.
• 1 zeigt eine vollkommen positive Beziehung zwischen den beiden Variablen an.

Im Allgemeinen gilt: Je weiter ein Phi-Koeffizient von Null entfernt ist, desto stärker ist die Beziehung zwischen den beiden Variablen.

Mit anderen Worten: Je weiter ein Phi-Koeffizient von Null entfernt ist, desto mehr Hinweise gibt es auf ein systematisches Muster zwischen den beiden Variablen.

Zusätzliche Ressourcen

Eine Einführung in den Phi-Koeffizienten
Rechner für den Phi-Koeffizienten