Was ist eine wahrscheinlichkeitsmassenfunktion (pmf) in der statistik?

Eine Wahrscheinlichkeitsmassenfunktion , oft als PMF abgekürzt, gibt uns die Wahrscheinlichkeit an, mit der eine diskrete Zufallsvariable einen bestimmten Wert annimmt.

Angenommen, wir würfeln einmal. Wenn wir x die Zahl bezeichnen, auf der der Würfel landet, dann lässt sich die Wahrscheinlichkeit, dass x gleich verschiedenen Werten ist, wie folgt beschreiben:

• P(X=1): 1/6
• P(X=2): 1/6
• P(X=3): 1/6
• P(X=4): 1/6
• P(X=5): 1/6
• P(X=6): 1/6

Es besteht die gleiche Chance, dass die Würfel auf einer beliebigen Zahl zwischen 1 und 6 landen.

So würden wir diese Wahrscheinlichkeiten als Wahrscheinlichkeitsmassenfunktion schreiben:

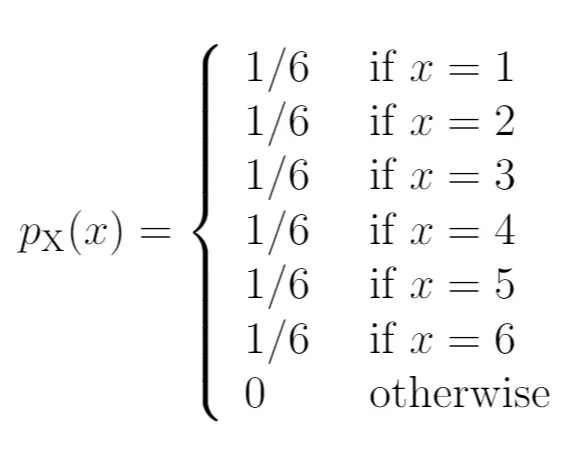
Die linke Seite des Diagramms zeigt die mit den Ergebnissen auf der rechten Seite verbundenen Wahrscheinlichkeiten:

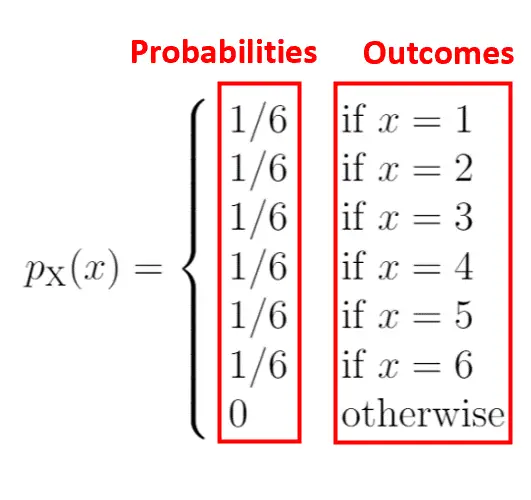
Ein Merkmal einer Wahrscheinlichkeitsmassenfunktion ist, dass sich alle Wahrscheinlichkeiten zu 1 summieren müssen. Sie werden feststellen, dass diese PMF diese Bedingung erfüllt:

Summe der Wahrscheinlichkeiten = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.

Die Unterstützung einer Wahrscheinlichkeitsmassenfunktion bezieht sich auf die Wertemenge, die die diskrete Zufallsvariable annehmen kann. In diesem Beispiel wäre die Unterstützung {1, 2, 3, 4, 5, 6}, da der Wert des Würfels jeden dieser Werte annehmen kann.

Außerhalb der Unterstützung beträgt der PMF-Wert Null. Beispielsweise ist die Wahrscheinlichkeit, dass der Würfel auf „0“, „7“ oder „8“ landet, Null, da keine dieser Zahlen in der Klammer enthalten ist.

Wahrscheinlichkeitsmassenfunktionen in der Praxis

Die beiden in der Praxis häufigsten Beispiele für Wahrscheinlichkeitsmassenfunktionen betreffen die Binomialverteilung und die Poisson-Verteilung .

Binomialverteilung

Wenn eine Zufallsvariable X einer Binomialverteilung folgt, kann die Erfolgswahrscheinlichkeit von X = k mit der folgenden Formel ermittelt werden:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Gold:

• n: Anzahl der Versuche
• k: Anzahl der Erfolge
• p: Erfolgswahrscheinlichkeit bei einem bestimmten Versuch
• _n C _k : die Anzahl der Möglichkeiten, in n Versuchen k Erfolge zu erzielen

Angenommen, wir werfen dreimal eine Münze. Wir können die obige Formel verwenden, um die Wahrscheinlichkeit zu bestimmen, bei diesen drei Würfen 0, 1, 2 und 3 Kopf zu erhalten:

• P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125
• P(X=1) = ₃ C ₁ * 0,5 ¹ * (1-0,5) ^3-1 = 1 * 1 * (0,5) ² = 0,375
• P(X=2) = ₃ C ₂ * 0,5 ² * (1-0,5) ^3-2 = 1 * 1 * (0,5) ¹ = 0,375
• P(X=3) = ₃ C ₃ * 0,5 ³ * (1-0,5) ^3-3 = 1 * 1 * (0,5) ⁰ = 0,125

Fischverteilung

Wenn eine Zufallsvariable X einer Poisson-Verteilung folgt, kann die Erfolgswahrscheinlichkeit von X = k mit der folgenden Formel ermittelt werden:

P(X=k) = λ ^k * e ^{– λ} / k!

Gold:

• λ: durchschnittliche Anzahl von Erfolgen, die während eines bestimmten Intervalls auftreten
• k: Anzahl der Erfolge
• e: eine Konstante, die ungefähr 2,71828 entspricht

Angenommen, in einem bestimmten Krankenhaus gibt es durchschnittlich zwei Geburten pro Stunde. Wir können die obige Formel verwenden, um die Wahrscheinlichkeit zu bestimmen, 0, 1, 2, 3 Geburten usw. zu erleben. in einer bestimmten Stunde:

• P(X=0) = 2 ⁰ * e ^{– 2} / 0! = 0,1353
• P(X=1) = 2 ¹ * e ^{– 2} / 1! = 0,2707
• P(X=2) = 2 ² * e ^{– 2} / 2! = 0,2707
• P(X=3) = 2 ³ * e ^{– 2} / 3! = 0,1805

Sehen Sie sich ein PMF an

Wahrscheinlichkeitsmassenfunktionen visualisieren wir oft mit Balkendiagrammen.

Das folgende Balkendiagramm zeigt beispielsweise die Wahrscheinlichkeiten, die mit der Anzahl der Geburten pro Stunde für die im vorherigen Beispiel beschriebene Poisson-Verteilung verbunden sind:

Beachten Sie, dass die Zahl der Geburten bis ins Unendliche reichen könnte, die Wahrscheinlichkeiten jedoch nach 10 so gering werden, dass Sie sie nicht einmal in einem Balkendiagramm sehen können.

Eigenschaften eines PMF

Eine Wahrscheinlichkeitsmassenfunktion hat die folgenden Eigenschaften:

1. Alle Wahrscheinlichkeiten sind positiv. Beispielsweise ist die Wahrscheinlichkeit, dass ein Würfel zwischen 1 und 6 fällt, positiv, während die Wahrscheinlichkeit aller anderen Ergebnisse Null ist.

2. Alle Ergebnisse haben eine Wahrscheinlichkeit zwischen 0 und 1. Beispielsweise beträgt die Wahrscheinlichkeit, dass ein Würfel zwischen 1 und 6 fällt, 1/6 oder 0,1666666 für jedes Ergebnis.

3. Die Summe aller Wahrscheinlichkeiten muss 1 sein. Beispielsweise beträgt die Summe der Wahrscheinlichkeiten, dass ein Würfel auf eine bestimmte Zahl fällt, 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1. /6 = 1.

Zusätzliche Ressourcen

Was sind Zufallsvariablen?
CDF oder PDF: Was ist der Unterschied?
Eine Einführung in die Binomialverteilung
Eine Einführung in die Poisson-Verteilung