So berechnen sie ein poisson-konfidenzintervall (schritt für schritt)

Die Poisson-Verteilung ist eine Wahrscheinlichkeitsverteilung, die zur Modellierung der Wahrscheinlichkeit des Auftretens einer bestimmten Anzahl von Ereignissen während eines festen Zeitintervalls verwendet wird, wenn bekannt ist, dass die Ereignisse unabhängig voneinander und mit einer konstanten Durchschnittsrate auftreten.

Während es nützlich ist, die durchschnittliche Anzahl der Vorkommnisse eines Poisson-Prozesses zu kennen, kann es noch nützlicher sein, ein Konfidenzintervall um die durchschnittliche Anzahl der Vorkommnisse zu haben.

Nehmen wir zum Beispiel an, wir sammeln an einem beliebigen Tag Daten in einem Callcenter und stellen fest, dass die durchschnittliche Anzahl der Anrufe pro Stunde 15 beträgt.

Da wir die Daten nur für einen einzigen Tag erhoben haben, können wir nicht sicher sein, dass das Callcenter das ganze Jahr über durchschnittlich 15 Anrufe pro Stunde erhält.

Wir können jedoch die folgende Formel verwenden, um ein Konfidenzintervall für die durchschnittliche Anzahl von Anrufen pro Stunde zu berechnen:

Poisson-Konfidenzintervallformel

Konfidenzintervall = [0,5*X ² _{2N, α/2} , 0,5*X ² _{2(N+1), 1-α/2} ]

Gold:

• X ² : Kritischer Wert des Chi-Quadrats
• N: Die Anzahl der beobachteten Ereignisse
• α: das Signifikanzniveau

Das folgende Schritt-für-Schritt-Beispiel veranschaulicht, wie ein 95 %-Poisson-Konfidenzintervall in der Praxis berechnet wird.

Schritt 1: Beobachtete Ereignisse zählen

Angenommen, wir berechnen die durchschnittliche Anzahl der Anrufe pro Stunde in einem Callcenter auf 15. Also ist N = 15 .

Und da wir ein Konfidenzintervall von 95 % berechnen, verwenden wir in den folgenden Berechnungen α = 0,05 .

Schritt 2: Finden Sie die untere Grenze des Konfidenzintervalls

Die untere Grenze des Konfidenzintervalls wird wie folgt berechnet:

• Untere Grenze = 0,5*X ² _{2N, α/2}
• Untere Grenze = 0,5*X ² _{2(15), 0,975}
• Untergrenze = 0,5*X ² _{30, 0,975}
• Untergrenze = 0,5*16,791
• Untergrenze = 8,40

Hinweis: Wir haben den Rechner für den kritischen Chi-Quadrat-Wert verwendet, um X ² _{30, 0,975} zu berechnen.

Schritt 3: Finden Sie die Obergrenze des Konfidenzintervalls

Die Obergrenze des Konfidenzintervalls wird wie folgt berechnet:

• Obergrenze = 0,5*X ² _{2(N+1), 1-α/2}
• Obergrenze = 0,5*X ² _{2(15+1), 0,025}
• Obergrenze = 0,5*X ² _{32, 0,025}
• Obergrenze = 0,5*49,48
• Obergrenze = 24,74

Hinweis: Wir haben den Rechner für den kritischen Chi-Quadrat-Wert verwendet, um X ² _32.0.025 zu berechnen.

Schritt 4: Finden Sie das Konfidenzintervall

Unter Verwendung der zuvor berechneten Unter- und Obergrenzen ergibt sich für unser 95 %-Poisson-Konfidenzintervall folgendes Ergebnis:

• 95 % KI = [8,40, 24,74]

Das bedeutet, dass wir zu 95 % sicher sind, dass die tatsächliche durchschnittliche Anzahl der Anrufe, die das Callcenter pro Stunde erhält, zwischen 8,40 und 24,74 Anrufen liegt.

Bonus: Fisch-Konfidenzintervall-Rechner

Fühlen Sie sich frei, diesen Poisson-Konfidenzintervall-Rechner zu verwenden, um automatisch ein Poisson-Konfidenzintervall zu berechnen.

So ermitteln Sie beispielsweise mit diesem Rechner das Poisson-Konfidenzintervall, das wir gerade manuell berechnet haben:

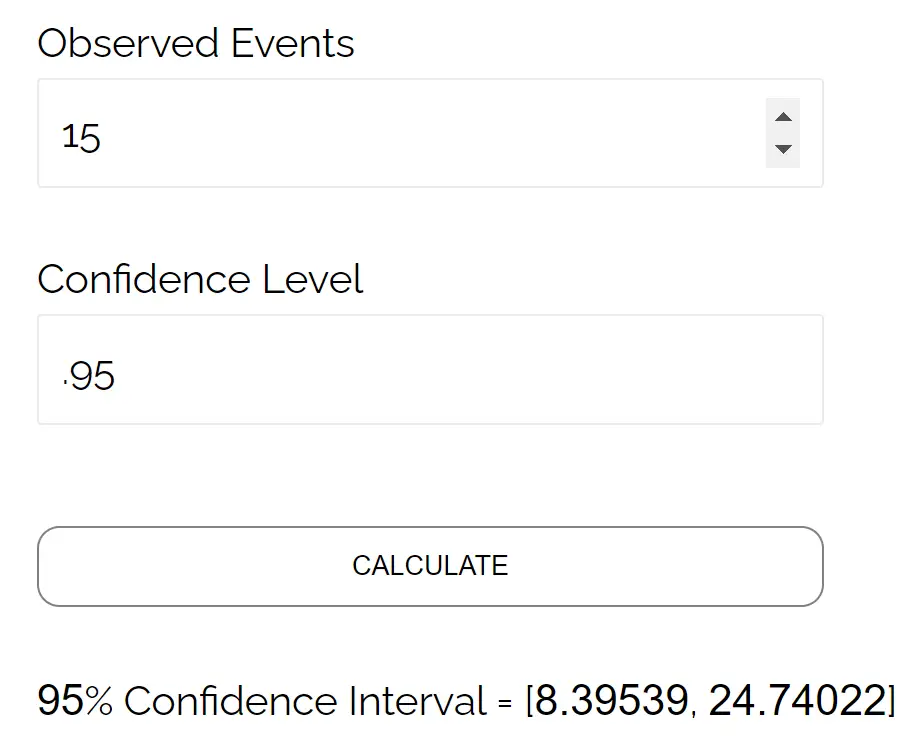
Beachten Sie, dass die Ergebnisse dem Konfidenzintervall entsprechen, das wir manuell berechnet haben.