So führen sie eine polynomregression in python durch

Die Regressionsanalyse wird verwendet, um die Beziehung zwischen einer oder mehreren erklärenden Variablen und einer Antwortvariablen zu quantifizieren.

Die gebräuchlichste Art der Regressionsanalyse ist dieeinfache lineare Regression , die verwendet wird, wenn eine Prädiktorvariable und eine Antwortvariable in einer linearen Beziehung stehen.

Manchmal ist die Beziehung zwischen einer Prädiktorvariablen und einer Antwortvariablen jedoch nichtlinear.

Beispielsweise kann die wahre Beziehung quadratisch sein:

Oder es kann kubisch sein:

In diesen Fällen ist es sinnvoll, eine polynomielle Regression zu verwenden, die die nichtlineare Beziehung zwischen Variablen berücksichtigen kann.

In diesem Tutorial wird erläutert, wie Sie eine Polynomregression in Python durchführen.

Beispiel: Polynomielle Regression in Python

Angenommen, wir haben die folgende Prädiktorvariable (x) und Antwortvariable (y) in Python:

 x = [2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12]
y = [18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29]

Wenn wir ein einfaches Streudiagramm dieser Daten erstellen, können wir erkennen, dass die Beziehung zwischen x und y eindeutig nicht linear ist:

 import matplotlib.pyplot as plt

#create scatterplot 
plt.scatter(x, y)

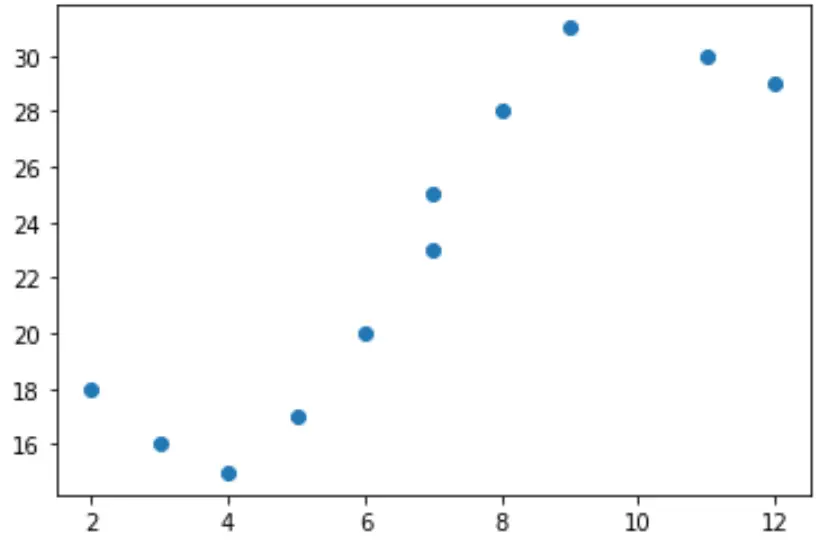
Es wäre daher nicht sinnvoll, ein lineares Regressionsmodell an diese Daten anzupassen. Stattdessen können wir versuchen, ein polynomiales Regressionsmodell mit Grad 3 anzupassen, indem wir die Funktion numpy.polyfit() verwenden:

 import numpy as np

#polynomial fit with degree = 3
model = np.poly1d(np.polyfit(x, y, 3))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 12, 50)
plt.scatter(x, y)
plt.plot(polyline, model(polyline))
plt.show() 

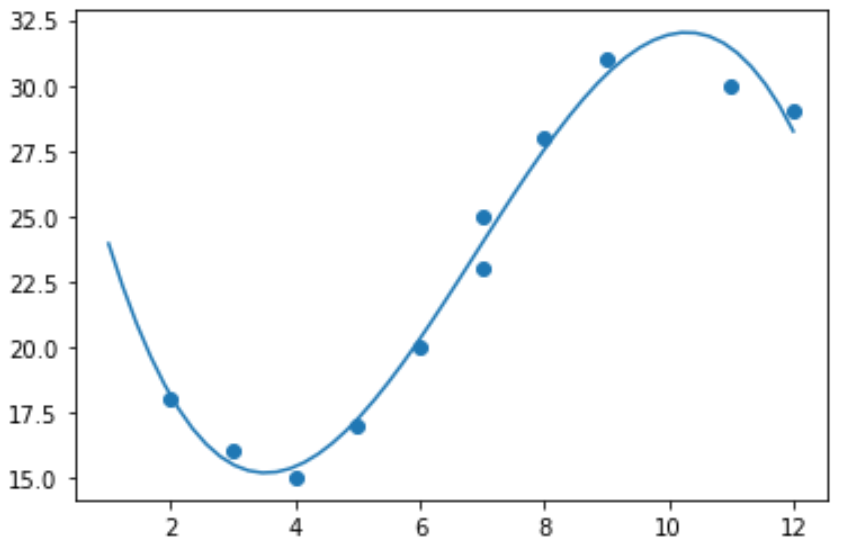
Wir können die angepasste polynomiale Regressionsgleichung erhalten, indem wir die Modellkoeffizienten drucken:

 print(model)

poly1d([ -0.10889554, 2.25592957, -11.83877127, 33.62640038])

Die angepasste polynomiale Regressionsgleichung lautet:

y = -0,109x ³ + 2,256x ² – 11,839x + 33,626

Diese Gleichung kann verwendet werden, um den erwarteten Wert der Antwortvariablen bei gegebenem Wert der erklärenden Variablen zu ermitteln.

Angenommen, x = 4. Der erwartete Wert für die Antwortvariable y wäre:

y = -0,109(4) ³ + 2,256(4) ² – 11,839(4) + 33,626= 15,39 .

Wir können auch eine kurze Funktion schreiben, um das R-Quadrat des Modells zu erhalten, das den Anteil der Varianz in der Antwortvariablen darstellt, der durch die Prädiktorvariablen erklärt werden kann.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = numpy.polyfit(x, y, degree)
    p = numpy.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = numpy.sum(y)/len(y)
    ssreg = numpy.sum((yhat-ybar)**2)
    sstot = numpy.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(x, y, 3)

{'r_squared': 0.9841113454245183}

In diesem Beispiel beträgt das R-Quadrat des Modells 0,9841 .

Dies bedeutet, dass 98,41 % der Variation der Antwortvariablen durch die Prädiktorvariablen erklärt werden können.