Polynomielle regression in r (schritt für schritt)
Die polynomielle Regression ist eine Technik, die wir verwenden können, wenn die Beziehung zwischen einer Prädiktorvariablen und einer Antwortvariablen nichtlinear ist.
Diese Art der Regression hat die Form:
Y = β 0 + β 1 X + β 2 X 2 + … + β h
wobei h der „Grad“ des Polynoms ist.
Dieses Tutorial bietet ein schrittweises Beispiel für die Durchführung einer Polynomregression in R.
Schritt 1: Erstellen Sie die Daten
Für dieses Beispiel erstellen wir einen Datensatz, der die Anzahl der gelernten Stunden und die Abschlussprüfungsnote für eine Klasse mit 50 Schülern enthält:
#make this example reproducible set.seed(1) #create dataset df <- data.frame(hours = runif (50, 5, 15), score=50) df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2) #view first six rows of data head(data) hours score 1 7.655087 64.30191 2 8.721239 70.65430 3 10.728534 73.66114 4 14.082078 86.14630 5 7.016819 59.81595 6 13.983897 83.60510
Schritt 2: Visualisieren Sie die Daten
Bevor wir ein Regressionsmodell an die Daten anpassen, erstellen wir zunächst ein Streudiagramm, um die Beziehung zwischen Lernstunden und Prüfungsergebnis zu visualisieren:
library (ggplot2) ggplot(df, aes (x=hours, y=score)) + geom_point()
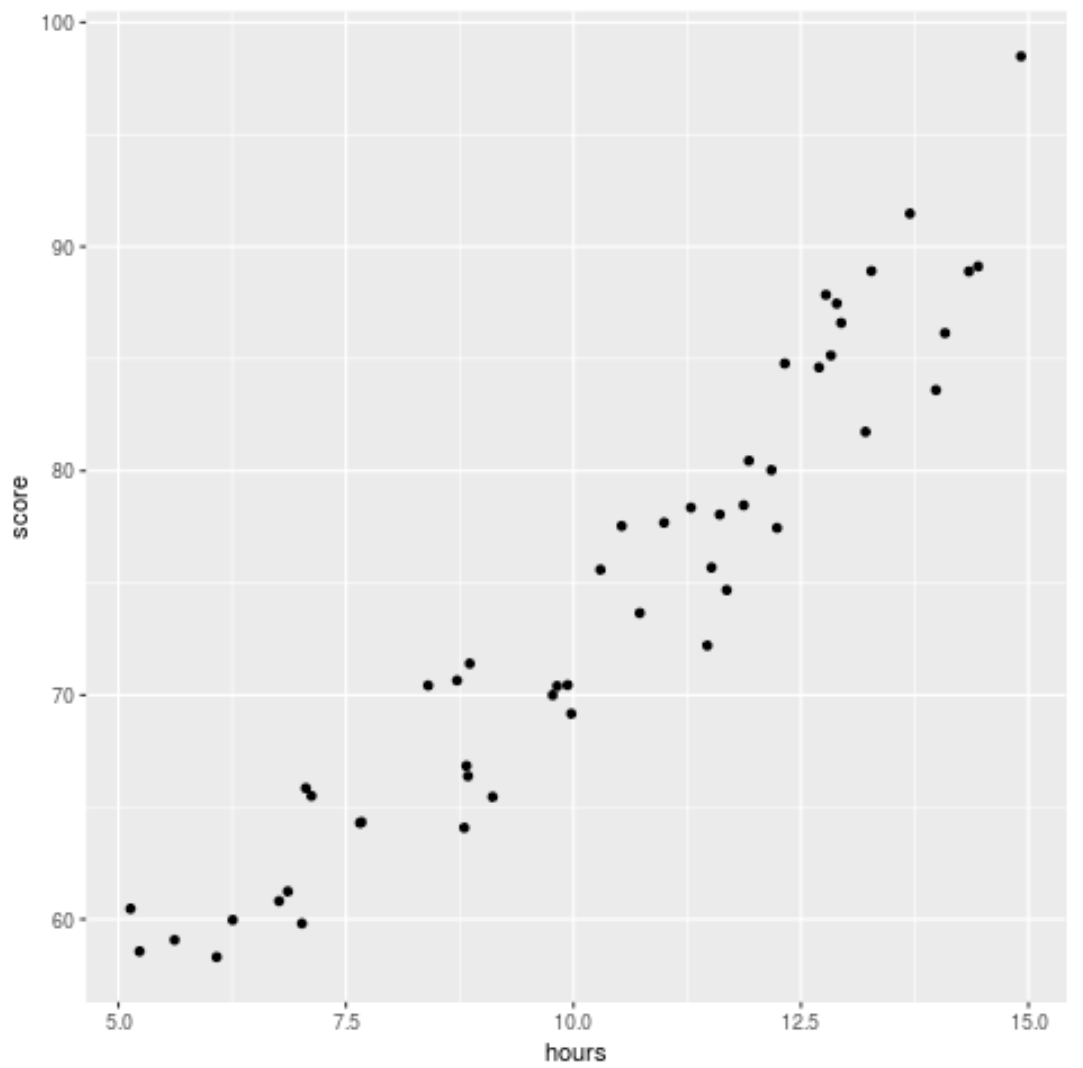
Wir können sehen, dass die Daten eine leicht quadratische Beziehung aufweisen, was darauf hindeutet, dass die polynomiale Regression möglicherweise besser zu den Daten passt als die einfache lineare Regression.
Schritt 3: Polynomielle Regressionsmodelle anpassen
Als nächstes passen wir fünf verschiedene polynomiale Regressionsmodelle mit den Graden h = 1…5 an und verwenden eine k-fache Kreuzvalidierung mit k = 10 Mal, um den MSE-Test für jedes Modell zu berechnen:
#randomly shuffle data
df.shuffled <- df[ sample ( nrow (df)),]
#define number of folds to use for k-fold cross-validation
K <- 10
#define degree of polynomials to fit
degree <- 5
#create k equal-sized folds
folds <- cut( seq (1, nrow (df.shuffled)), breaks=K, labels= FALSE )
#create object to hold MSE's of models
mse = matrix(data=NA,nrow=K,ncol=degree)
#Perform K-fold cross validation
for (i in 1:K){
#define training and testing data
testIndexes <- which (folds==i,arr.ind= TRUE )
testData <- df.shuffled[testIndexes, ]
trainData <- df.shuffled[-testIndexes, ]
#use k-fold cv to evaluate models
for (j in 1:degree){
fit.train = lm (score ~ poly (hours,d), data=trainData)
fit.test = predict (fit.train, newdata=testData)
mse[i,j] = mean ((fit.test-testData$score)^2)
}
}
#find MSE for each degree
colMeans(mse)
[1] 9.802397 8.748666 9.601865 10.592569 13.545547
Aus dem Ergebnis können wir den MSE-Test für jedes Modell sehen:
- MSE-Test mit Grad h = 1: 9,80
- MSE-Test mit Grad h = 2: 8,75
- MSE-Test mit Abschluss h = 3: 9,60
- MSE-Test mit Abschluss h = 4: 10,59
- MSE-Test mit Abschluss h = 5: 13,55
Das Modell mit dem niedrigsten Test-MSE erwies sich als polynomiales Regressionsmodell mit Grad h = 2.
Dies entspricht unserer Intuition aus dem ursprünglichen Streudiagramm: Ein quadratisches Regressionsmodell passt am besten zu den Daten.
Schritt 4: Analysieren Sie das endgültige Modell
Schließlich können wir die Koeffizienten des Modells mit der besten Leistung erhalten:
#fit best model best = lm (score ~ poly (hours,2, raw= T ), data=df) #view summary of best model summary(best) Call: lm(formula = score ~ poly(hours, 2, raw = T), data = df) Residuals: Min 1Q Median 3Q Max -5.6589 -2.0770 -0.4599 2.5923 4.5122 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 54.00526 5.52855 9.768 6.78e-13 *** poly(hours, 2, raw = T)1 -0.07904 1.15413 -0.068 0.94569 poly(hours, 2, raw = T)2 0.18596 0.05724 3.249 0.00214 ** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Aus dem Ergebnis können wir ersehen, dass das endgültig angepasste Modell wie folgt aussieht:
Punktzahl = 54,00526 – 0,07904*(Stunden) + 0,18596*(Stunden) 2
Mit dieser Gleichung können wir die Punktzahl schätzen, die ein Schüler basierend auf der Anzahl der gelernten Stunden erhält.
Beispielsweise sollte ein Student, der 10 Stunden lernt, eine Note von 71,81 bekommen:
Punktzahl = 54,00526 – 0,07904*(10) + 0,18596*(10) 2 = 71,81
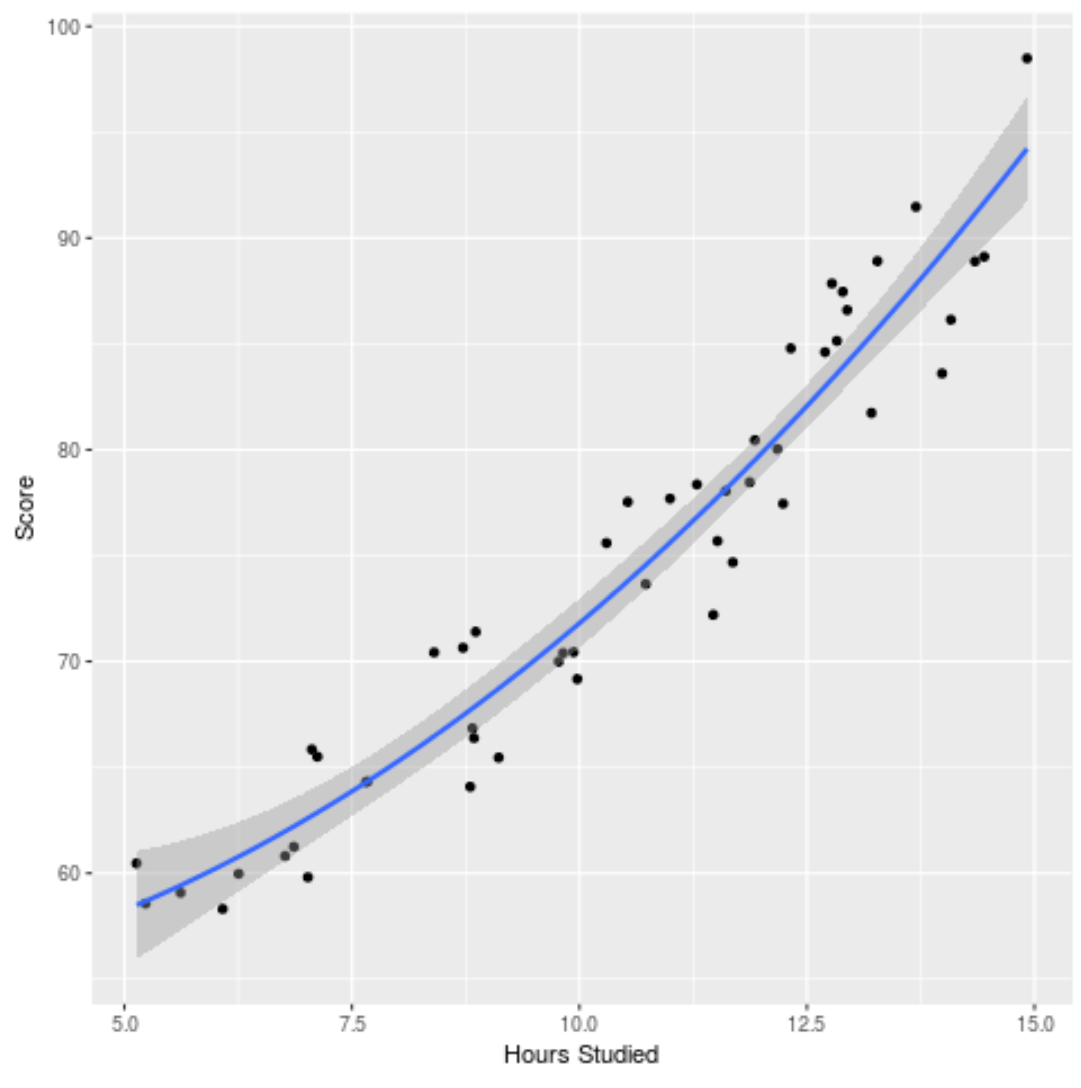
Wir können das angepasste Modell auch grafisch darstellen, um zu sehen, wie gut es zu den Rohdaten passt:
ggplot(df, aes (x=hours, y=score)) + geom_point() + stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + xlab(' Hours Studied ') + ylab(' Score ')
Den vollständigen R-Code, der in diesem Beispiel verwendet wird, finden Sie hier .