So führen sie eine polynomregression mit scikit-learn durch

Die polynomielle Regression ist eine Technik, die wir verwenden können, wenn die Beziehung zwischen einer Prädiktorvariablen und einer Antwortvariablen nichtlinear ist.

Diese Art der Regression hat die Form:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

wobei h der „Grad“ des Polynoms ist.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie Sie mit sklearn eine Polynomregression in Python durchführen.

Schritt 1: Erstellen Sie die Daten

Erstellen wir zunächst zwei NumPy-Arrays, um die Werte eines Prädiktors und einer Antwortvariablen zu speichern:

 import matplotlib. pyplot as plt
import numpy as np

#define predictor and response variables
x = np. array ([2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12])
y = np. array ([18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29])

#create scatterplot to visualize relationship between x and y
plt. scatter (x,y)

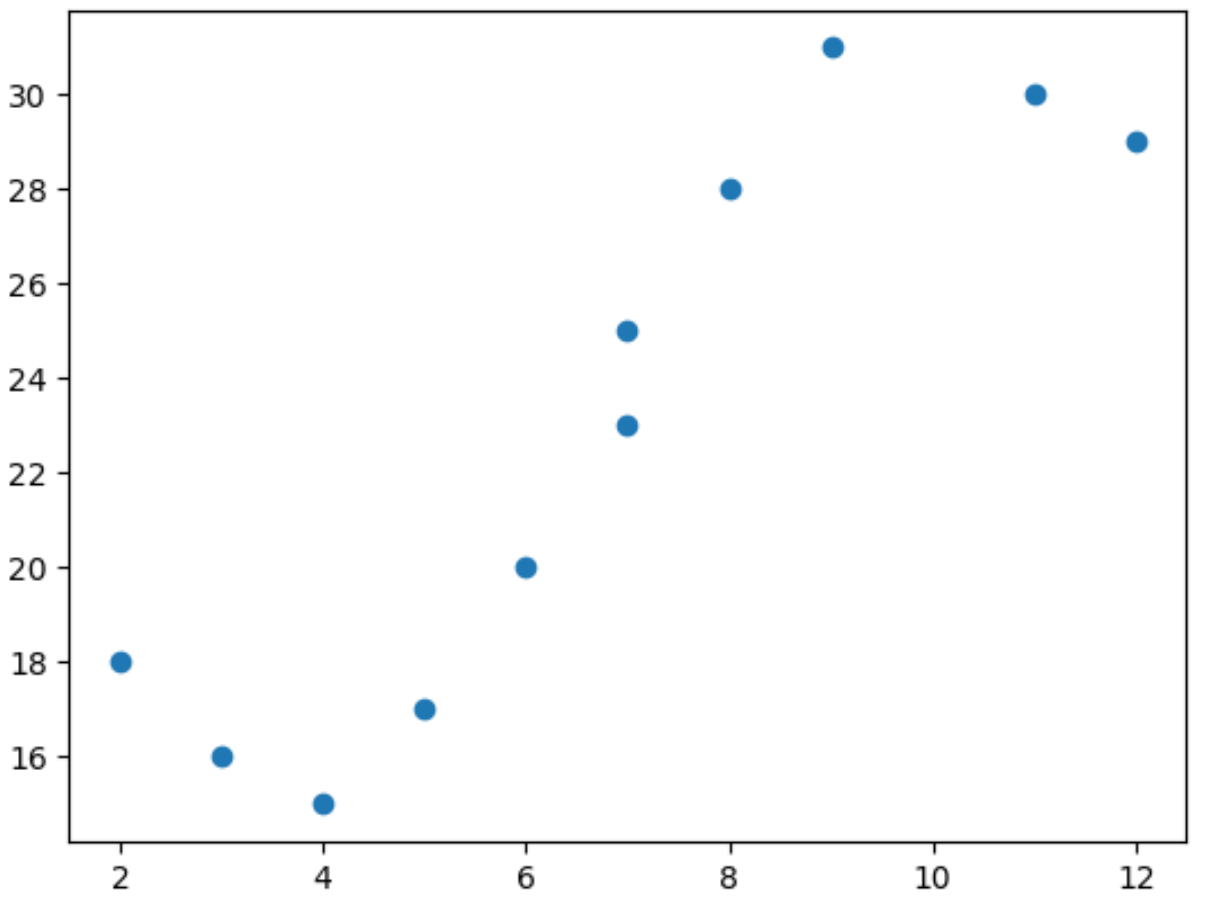
Aus dem Streudiagramm können wir erkennen, dass die Beziehung zwischen x und y nicht linear ist.

Daher ist es eine gute Idee, ein polynomiales Regressionsmodell an die Daten anzupassen, um die nichtlineare Beziehung zwischen den beiden Variablen zu erfassen.

Schritt 2: Passen Sie das polynomiale Regressionsmodell an

Der folgende Code zeigt, wie sklearn-Funktionen verwendet werden, um ein Polynom-Regressionsmodell 3. Grades an diesen Datensatz anzupassen:

 from sklearn. preprocessing import PolynomialFeatures
from sklearn. linear_model import LinearRegression

#specify degree of 3 for polynomial regression model
#include bias=False means don't force y-intercept to equal zero
poly = PolynomialFeatures(degree= 3 , include_bias= False )

#reshape data to work properly with sklearn
poly_features = poly. fit_transform ( x.reshape (-1, 1))

#fit polynomial regression model
poly_reg_model = LinearRegression()
poly_reg_model. fit (poly_features,y)

#display model coefficients
print (poly_reg_model. intercept_ , poly_reg_model. coef_ )

33.62640037532282 [-11.83877127 2.25592957 -0.10889554]

Mithilfe der in der letzten Zeile angezeigten Modellkoeffizienten können wir die angepasste polynomiale Regressionsgleichung wie folgt schreiben:

y = -0,109x ³ + 2,256x ² – 11,839x + 33,626

Diese Gleichung kann verwendet werden, um den erwarteten Wert der Antwortvariablen bei gegebenem Wert der vorhergesagten Variablen zu ermitteln.

Wenn x beispielsweise 4 ist, wäre der erwartete Wert für die Antwortvariable y 15,39:

y = -0,109(4) ³ + 2,256(4) ² – 11,839(4) + 33,626= 15,39

Hinweis : Um ein polynomiales Regressionsmodell mit einem anderen Grad anzupassen, ändern Sie einfach den Wert des Gradarguments in der Funktion PolynomialFeatures() .

Schritt 3: Visualisieren Sie das polynomiale Regressionsmodell

Schließlich können wir ein einfaches Diagramm erstellen, um das an die ursprünglichen Datenpunkte angepasste polynomielle Regressionsmodell zu visualisieren:

 #use model to make predictions on response variable
y_predicted = poly_reg_model. predict (poly_features)

#create scatterplot of x vs. y
plt. scatter (x,y)

#add line to show fitted polynomial regression model
plt. plot (x,y_predicted,color=' purple ')

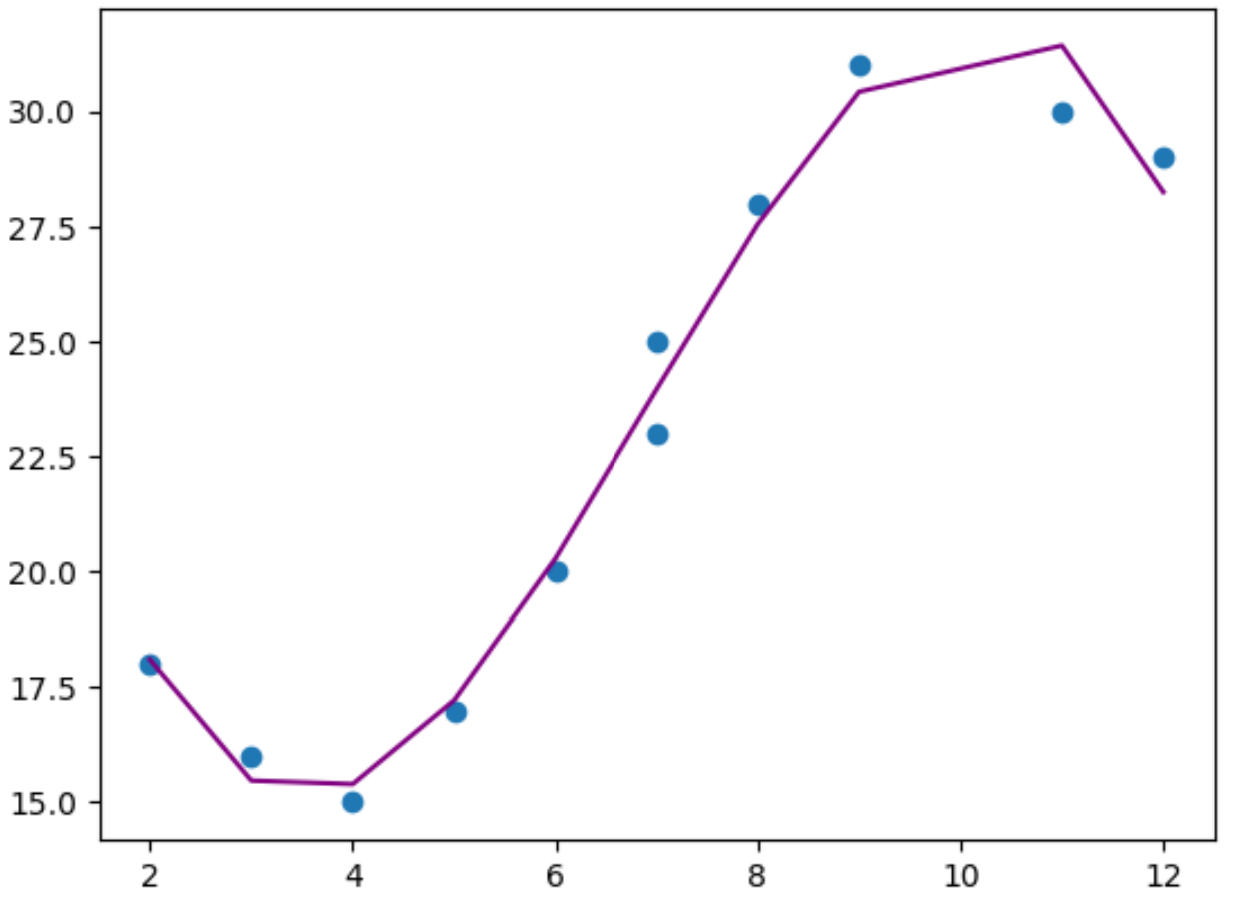
Aus der Grafik können wir ersehen, dass das polynomiale Regressionsmodell gut zu den Daten zu passen scheint, ohne dass es zu einer Überanpassung kommt .

Hinweis : Die vollständige Dokumentation für die Funktion sklearn PolynomialFeatures() finden Sie hier .

Zusätzliche Ressourcen

Die folgenden Tutorials erklären, wie Sie andere häufige Aufgaben mit sklearn ausführen:

So extrahieren Sie Regressionskoeffizienten aus sklearn
So berechnen Sie die ausgewogene Präzision mit sklearn
So interpretieren Sie den Klassifizierungsbericht in Sklearn