Positive korrelation

In diesem Artikel erfahren Sie, was positive Korrelation in der Statistik bedeutet, Beispiele für Variablen mit positiver Korrelation und welche Unterschiede zwischen anderen Korrelationsarten bestehen.

Was ist eine positive Korrelation?

In der Statistik ist eine positive Korrelation eine Art Korrelation zwischen zwei verschiedenen Variablen. Genauer gesagt bedeutet eine positive Korrelation zwischen zwei Variablen, dass wenn der Wert einer Variablen steigt, auch die andere Variable zunimmt.

Damit eine Korrelation zwischen zwei Variablen als positiv angesehen wird, muss der Wert des Korrelationskoeffizienten zwischen 0 (nicht enthalten) und 1 (einschließlich) liegen.

Beachten Sie, dass positive Korrelation auch als direkte Korrelation bezeichnet werden kann.

Beispiel für positive Korrelation

In Anbetracht der Definition einer positiven Korrelation finden Sie unten ein Beispiel für zwei Variablen, die eine solche Korrelation aufweisen.

• In der folgenden Häufigkeitstabelle wurden die Mathematik- und Statistikergebnisse einer Stichprobe von 20 Schülern als Daten erfasst. Analysieren Sie die Beziehung zwischen den beiden Variablen.

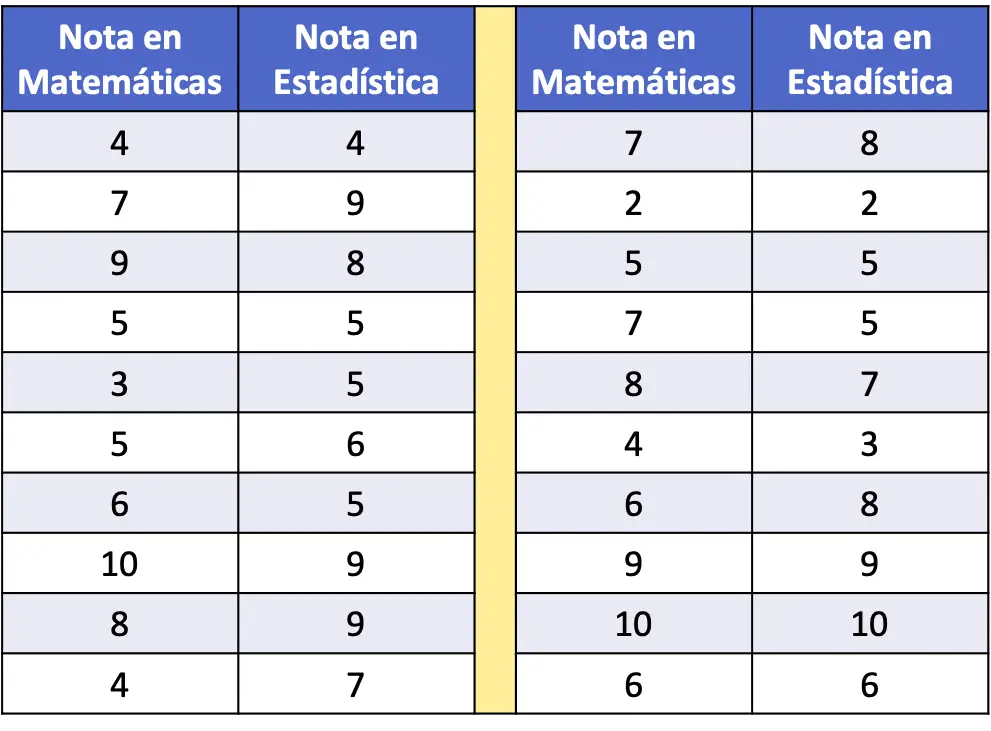
Vor der Berechnung des Korrelationskoeffizienten empfiehlt es sich, den statistischen Datensatz zur Vorerkundung zunächst in einem Streudiagramm darzustellen.

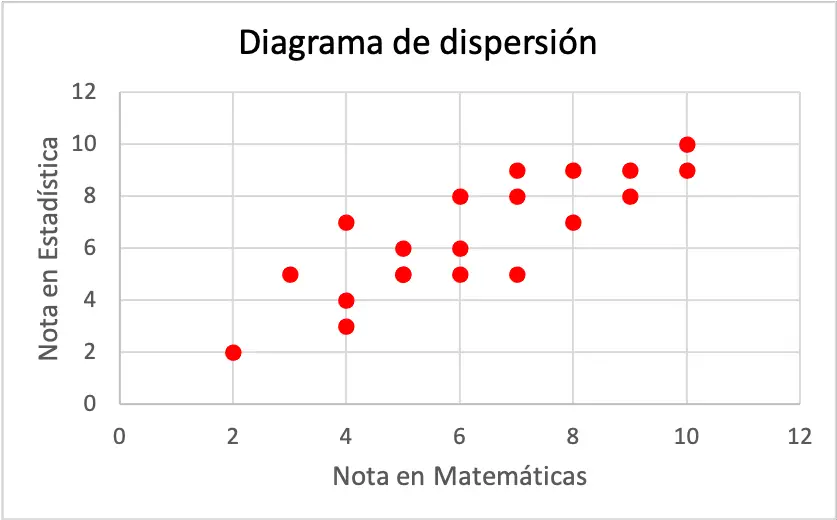
Wie die Grafik zeigt, scheint zwischen den beiden Variablen eine positive lineare Korrelation zu bestehen, da mit steigender Mathematiknote auch die Statistiknote steigt. Um jedoch die Art der Korrelation mit Sicherheit zu bestimmen, muss der Korrelationskoeffizient berechnet werden :

Der Wert des Pearson-Korrelationskoeffizienten ist größer als 0 und sehr nahe bei 1, die Korrelation zwischen den beiden untersuchten Variablen ist also tatsächlich positiv.

Interpretation der positiven Korrelation

Um die Bedeutung der positiven Korrelation in der Statistik vollständig zu verstehen, erfahren Sie in diesem Abschnitt, wie der Wert einer positiven Korrelation zwischen zwei Variablen interpretiert wird.

Je höher der Wert des Korrelationskoeffizienten ist, desto stärker korrelieren die beiden Variablen positiv. Wenn der Wert des Korrelationskoeffizienten also nahe bei 1 liegt, bedeutet dies, dass die Korrelation zwischen den beiden Variablen positiv und sehr stark ist.

Wenn andererseits der Wert des Korrelationskoeffizienten niedrig ist und nahe bei Null liegt, bedeutet dies, dass die Korrelation zwischen den beiden Variablen positiv, aber schwach ist. Selbst wenn der Korrelationskoeffizient null oder negativ wird, bedeutet dies, dass die Korrelation null bzw. negativ ist. Im Folgenden werden wir die Unterschiede zwischen diesen drei Korrelationstypen sehen.

Abschließend ist zu beachten, dass eine positive Korrelation keine Kausalität zwischen den Variablen bedeutet. Das heißt, wenn zwei Variablen eine positive Korrelation aufweisen, bedeutet dies, dass sie linear miteinander verbunden sind, eine Variable jedoch nicht unbedingt die Ursache für die andere ist.

Ähnlich wie im vorherigen Abschnitt korrelieren die Noten in Mathematik und Statistik positiv miteinander. Eine gute Note in Mathematik garantiert jedoch nicht automatisch eine gute Note in Statistik, sondern es müssen beide Fächer studiert werden. Zusammenfassend lässt sich sagen, dass die Note in Mathematik nicht die Ursache für die Note in Statistik ist, sondern dass die beiden Variablen lediglich miteinander verknüpft sind.

Positive, negative und Nullkorrelation

Neben einer positiven Korrelation können in der Statistik zwei Variablen auch eine negative oder keine Korrelation aufweisen. Daher werden wir in diesem Abschnitt sehen, wie diese drei Korrelationstypen unterschieden werden.

• Positive Korrelation : Eine Variable nimmt zu, wenn auch die andere zunimmt. Der Wert des Korrelationskoeffizienten liegt zwischen 0 (nicht enthalten) und 1 (einschließlich).
• Negative Korrelation : Wenn eine Variable zunimmt, nimmt die andere ab, und umgekehrt, wenn eine Variable abnimmt, nimmt die andere zu. Der Wert des Korrelationskoeffizienten liegt zwischen -1 (einschließlich) und 0 (nicht einschließlich).
• Nullkorrelation : Es besteht keine Beziehung zwischen den beiden Variablen. Der Korrelationskoeffizient ist gleich 0.

In den folgenden Diagrammen können Sie jeden dargestellten Korrelationstyp sehen: