So führen sie eine potenzregression in r durch (schritt für schritt)

Die Potenzregression ist eine Art nichtlineare Regression, die die folgende Form annimmt:

y = ^axb

Gold:

• y: die Antwortvariable
• x: die Vorhersagevariable
• a, b: die Regressionskoeffizienten, die die Beziehung zwischen x und y beschreiben

Diese Art der Regression wird verwendet, um Situationen zu modellieren, in denen die Antwortvariable gleich der Prädiktorvariablen potenziert ist.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie eine Potenzregression für einen bestimmten Datensatz in R durchgeführt wird.

Schritt 1: Erstellen Sie die Daten

Erstellen wir zunächst gefälschte Daten für zwei Variablen: x und y.

 #create data
x=1:20
y=c(1, 8, 5, 7, 6, 20, 15, 19, 23, 37, 33, 38, 49, 50, 56, 52, 70, 89, 97, 115)

Schritt 2: Visualisieren Sie die Daten

Als Nächstes erstellen wir ein Streudiagramm, um die Beziehung zwischen x und y zu visualisieren:

 #create scatterplot
plot(x, y) 

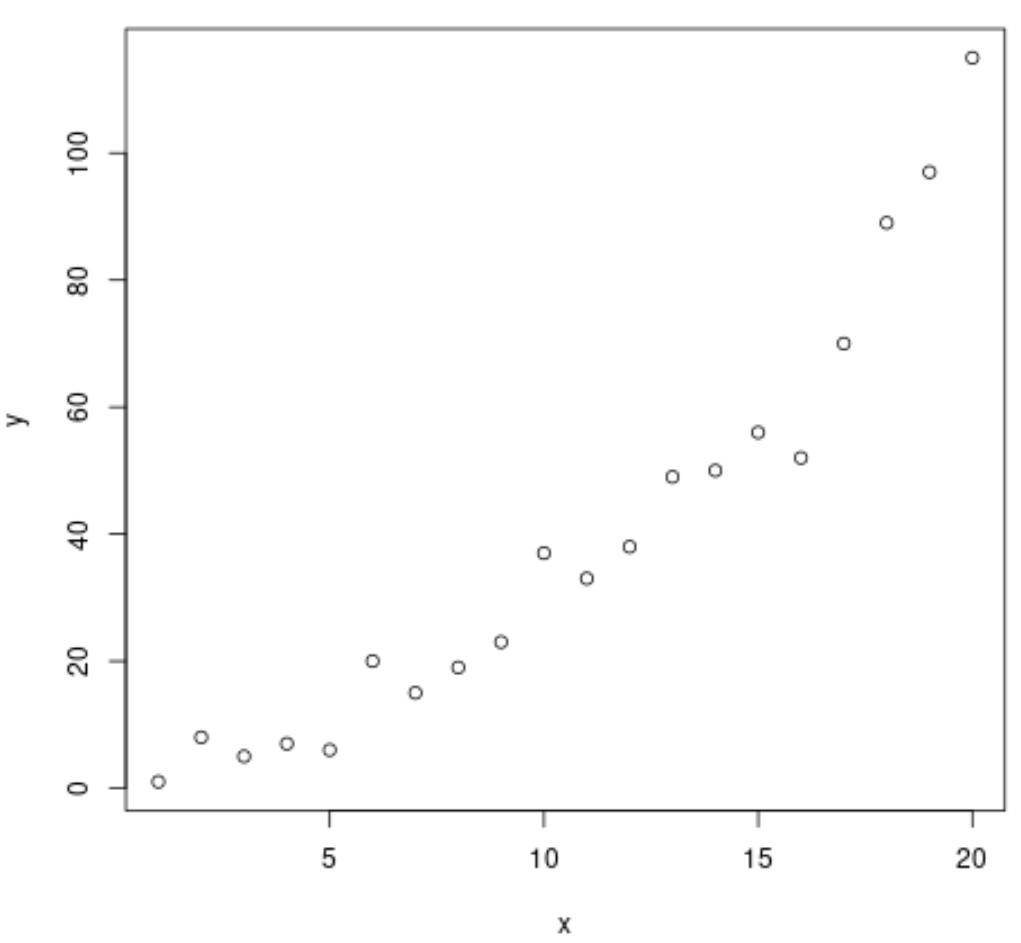
Die Grafik zeigt, dass zwischen den beiden Variablen ein klarer Machtzusammenhang besteht. Daher erscheint es sinnvoll, anstelle eines linearen Regressionsmodells eine Potenzregressionsgleichung an die Daten anzupassen.

Schritt 3: Passen Sie das Power-Regressionsmodell an

Als Nächstes verwenden wir die Funktion lm() , um ein Regressionsmodell an die Daten anzupassen, und geben an, dass R beim Anpassen des Modells das Antwortvariablenprotokoll und das Prädiktorvariablenprotokoll verwenden soll:

 #fit the model
model <- lm(log(y)~ log(x))

#view the output of the model
summary(model)

Call:
lm(formula = log(y) ~ log(x))

Residuals:
     Min 1Q Median 3Q Max 
-0.67014 -0.17190 -0.05341 0.16343 0.93186 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.15333 0.20332 0.754 0.461    
log(x) 1.43439 0.08996 15.945 4.62e-12 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3187 on 18 degrees of freedom
Multiple R-squared: 0.9339, Adjusted R-squared: 0.9302 
F-statistic: 254.2 on 1 and 18 DF, p-value: 4.619e-12

Der Gesamt-F-Wert des Modells beträgt 252,1 und der entsprechende p-Wert ist extrem niedrig (4,619e-12), was darauf hinweist, dass das Modell als Ganzes nützlich ist.

Anhand der Koeffizienten aus der Ausgabetabelle können wir sehen, dass die angepasste Leistungsregressionsgleichung wie folgt lautet:

ln(y) = 0,15333 + 1,43439ln(x)

Wenn wir e auf beide Seiten anwenden, können wir die Gleichung wie folgt umschreiben:

• y = e ^{0,15333 + 1,43439ln(x)}
• y = 1,1657x ^1,43439

Wir können diese Gleichung verwenden, um die Antwortvariable y basierend auf dem Wert der Prädiktorvariablen x vorherzusagen.

Wenn zum Beispiel x = 12, dann würden wir vorhersagen, dass y 41,167 wäre:

y = 1,1657(12) ^1,43439 = 41,167

Bonus: Fühlen Sie sich frei, diesen Online-Leistungsregressionsrechner zu verwenden, um die Leistungsregressionsgleichung für einen bestimmten Prädiktor und eine bestimmte Antwortvariable automatisch zu berechnen.

Zusätzliche Ressourcen

So führen Sie eine multiple lineare Regression in R durch
So führen Sie eine exponentielle Regression in R durch
So führen Sie eine logarithmische Regression in R durch