Was ist ein probenraum? definition und beispiele

Der Probenraum eines Experiments ist die Menge aller möglichen Ergebnisse des Experiments.

Angenommen, wir würfeln einmal. Der Beispielraum möglicher Ergebnisse umfasst:

Probenraum = 1, 2, 3, 4, 5, 6

Unter Verwendung der Notation schreiben wir das Beispielraumsymbol als kursives S und die Ergebnisse in Klammern wie folgt:

S = {1, 2, 3, 4, 5, 6}

Beispiele für Beispielräume

Hier sind einige weitere Beispiele für Beispielräume:

Beispiel 1: Zeichnen

Angenommen, wir werfen einmal eine Münze. Wenn wir annehmen, dass H = die Münze auf „Kopf“ landet und T = die Münze auf „Zahl“ landet, dann ist der Beispielraum für diesen Münzwurf:

S = {H, T}

Beispiel 2: Murmeln in einer Tüte

Angenommen, wir wählen zufällig eine Murmel aus einem Beutel mit drei Murmeln aus: einer roten Murmel, einer grünen Murmel und einer blauen Murmel. Wenn wir R = Rot, G = Grün und B = Blau lassen, dann ist der Probenraum:

S = {R, G, B}

Beispiel 3: Münzwurf und Würfelwurf

Angenommen, wir werfen eine Münze und würfeln gleichzeitig. Wenn wir H1 das Ergebnis eines „Head“ und einer „1“ darstellen lassen, dann ist der Probenraum für die Ergebnisse:

S = {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}

Das Grundprinzip des Zählens

Das Grundprinzip des Zählens ist eine Methode zur Berechnung der Gesamtzahl möglicher Ergebnisse eines Experiments.

Dieses Prinzip besagt, dass, wenn Ereignis A n unterschiedliche Ergebnisse hat und Ereignis B m unterschiedliche Ergebnisse hat, die Gesamtzahl der potenziellen Ergebnisse wie folgt berechnet werden kann:

Gesamtergebnisse = m * n

Beispiel 1: Münzwurf und Würfelwurf

Wenn wir beispielsweise eine Münze werfen und gleichzeitig einen Würfel werfen, kann die Gesamtzahl der Ergebnisse im Stichprobenraum wie folgt berechnet werden:

Gesamtergebnis = (2 Möglichkeiten, wie eine Münze landen kann) * (6 Möglichkeiten, wie ein Würfel landen kann) = 12 mögliche Ergebnisse.

Diese 12 Ergebnisse haben wir im vorherigen Beispiel geschrieben:

S = {H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}

Beispiel 2: Outfit-Kombinationen zählen

Dieses Prinzip kann auch verwendet werden, um Gesamtergebnisse in einem Stichprobenraum für mehr als zwei Ereignisse zu berechnen.

Angenommen, eine zufällige Schublade enthält drei verschiedene Hemden, vier verschiedene Hosen und zwei verschiedene Socken. Wenn wir ohne hinzusehen zufällig jeweils ein Kleidungsstück auswählen, errechnet sich die Gesamtzahl der möglichen Outfits wie folgt:

Gesamtoutfits = 3 * 4 * 2 = 24 mögliche Outfits

Beispielräume mit Baumdiagrammen visualisieren

Wenn die Anzahl der Ergebnisse in einem Stichprobenraum groß ist, kann es nützlich sein, ein Baumdiagramm zu erstellen, um die verschiedenen Ergebniskombinationen zu visualisieren.

Angenommen, ein Schrank enthält zwei verschiedene Hemden, zwei verschiedene Hosen und zwei verschiedene Socken. Wenn wir ohne hinzusehen zufällig jeweils ein Kleidungsstück auswählen, könnte sich die Gesamtzahl der möglichen Outfits wie folgt vorstellen:

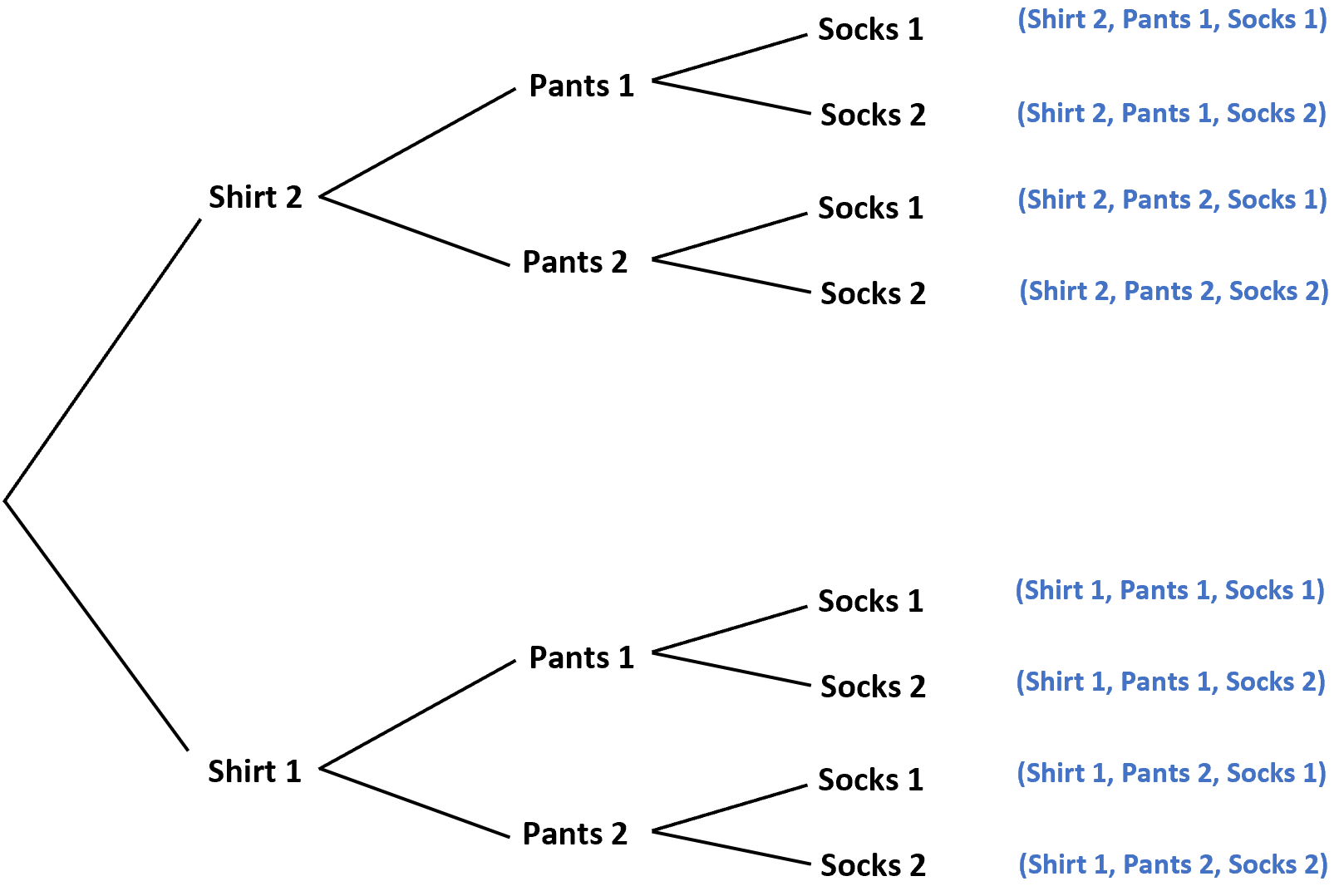
Dieses Diagramm hilft uns, die acht verschiedenen möglichen Ergebnisse im Beispielraum zu visualisieren.

Wir können auch das Grundprinzip des Zählens verwenden, um zu bestätigen, dass es acht verschiedene Ergebnisse geben muss:

Gesamtergebnis = 2 Hemden * 2 Hosen * 2 Socken = 8 mögliche Outfits

Berechnung von Ergebniswahrscheinlichkeiten in Stichprobenräumen

Sobald wir den Probenraum eines Experiments identifiziert haben, können wir die Wahrscheinlichkeit des Eintretens von Ereignis A mithilfe der folgenden Formel berechnen:

P(A) = (Probenraum von A) / (Gesamtprobenraum)

Angenommen, wir würfeln einmal. Der Beispielraum kann in der Form geschrieben werden:

S = {1, 2, 3, 4, 5, 6}

Wenn wir Ereignis A als die Landung des Würfels auf der Zahl „2“ definieren, dann kann der Probenraum von Ereignis A wie folgt geschrieben werden:

S = {2}

Somit lässt sich die Eintrittswahrscheinlichkeit von Ereignis A wie folgt berechnen:

P(A) = 1/6

Wenn wir Ereignis A als die Landung des Würfels auf einer geraden Zahl definieren, dann kann der Probenraum von Ereignis A wie folgt geschrieben werden:

S = {2, 4, 6}

Somit lässt sich die Eintrittswahrscheinlichkeit von Ereignis A wie folgt berechnen:

P(A) = 3/6