Was ist eine punktschätzung in der statistik?
In der Statistik sind wir häufig an der Messung von Populationsparametern interessiert, also Zahlen, die bestimmte Merkmale einer gesamten Population beschreiben.
Zwei der häufigsten Populationsparameter sind:
1. Bevölkerungsmittelwert: der Durchschnittswert einer Variablen in einer Bevölkerung (z. B. die durchschnittliche Körpergröße von Männern in einer bestimmten Stadt)
2. Bevölkerungsanteil: der Anteil einer Variablen in einer Bevölkerung (z. B. der Anteil der Einwohner eines Landkreises, die ein bestimmtes Gesetz unterstützen)
Selbst wenn wir diese Parameter messen wollen, ist es im Allgemeinen zu teuer und zeitaufwändig, Daten über jedes Individuum in einer Population zu sammeln.
Stattdessen nehmen wir eine Zufallsstichprobe aus der Grundgesamtheit und verwenden die Stichprobendaten, um den Grundgesamtheitsparameter zu schätzen.
Die Zahl, die wir in der Stichprobe zur Schätzung des Populationsparameters verwenden, wird als Punktschätzung bezeichnet. Dies ist unsere bestmögliche Schätzung des tatsächlichen Bevölkerungsparameters.
Die folgende Tabelle zeigt die Punktschätzung, die wir zur Schätzung der Populationsparameter verwenden:
| Die Maßnahme | Bevölkerungsparameter | Punktschätzung |
|---|---|---|
| Bedeuten | μ (Bevölkerungsdurchschnitt) | x (Stichprobendurchschnitt) |
| Anteil | π (Anteil der Bevölkerung) | p (Stichprobenanteil) |
Wir möchten Bevölkerungsparameter berechnen, aber da dies zu lange dauert und zu viel kostet, verwenden wir stattdessen Stichproben zur Berechnung von Punktschätzungen.
Nehmen wir zum Beispiel an, wir möchten das Durchschnittsgewicht einer bestimmten Schildkrötenart in Florida schätzen. Da es in Florida Tausende von Schildkröten gibt, wäre es äußerst zeitaufwändig und teuer, jede Schildkröte einzeln zu wiegen. Stattdessen könnten wir eine einfache Zufallsstichprobe von 50 Schildkröten nehmen und das Durchschnittsgewicht der Schildkröten in dieser Stichprobe verwenden, um den wahren Mittelwert der Population zu schätzen:

Wenn der Stichprobenmittelwert 150,4 Pfund beträgt, dann würde unsere Punktschätzung des wahren Populationsmittelwerts der gesamten Art 150,4 Pfund betragen.
Die Bedeutung repräsentativer Stichproben
Wenn wir eine Stichprobe aus einer Grundgesamtheit sammeln, möchten wir im Idealfall, dass die Stichprobe einer „Miniversion“ unserer Grundgesamtheit ähnelt.
Eine Stichprobe gilt als repräsentativ für eine Population , wenn die Merkmale der Individuen in der Stichprobe weitgehend mit den Merkmalen der Individuen in der Gesamtpopulation übereinstimmen.
Wenn dies geschieht, können wir die Ergebnisse der Stichprobe sicher auf die Gesamtpopulation übertragen und sagen, dass die Stichprobenpunktschätzung eine unvoreingenommene Schätzung des wahren Populationsparameters ist.
Punktschätzungen und Konfidenzintervalle
Obwohl eine Punktschätzung unsere bestmögliche Schätzung eines echten Populationsparameters darstellt, ist es unwahrscheinlich, dass sie genau dem Populationsparameter entspricht.
In unserem vorherigen Beispiel kann nicht garantiert werden, dass das Durchschnittsgewicht der Schildkröten in der Stichprobe genau mit dem Durchschnittsgewicht der Schildkröten in der gesamten Population übereinstimmt. Beispielsweise könnten wir eine Stichprobe voller Schildkröten mit geringem Gewicht oder vielleicht eine Stichprobe voller schwerer Schildkröten auswählen.
Um diese Unsicherheit zu erfassen, können wir ein Konfidenzintervall erstellen – einen Wertebereich, der wahrscheinlich einen Populationsparameter mit einem bestimmten Konfidenzniveau enthält.
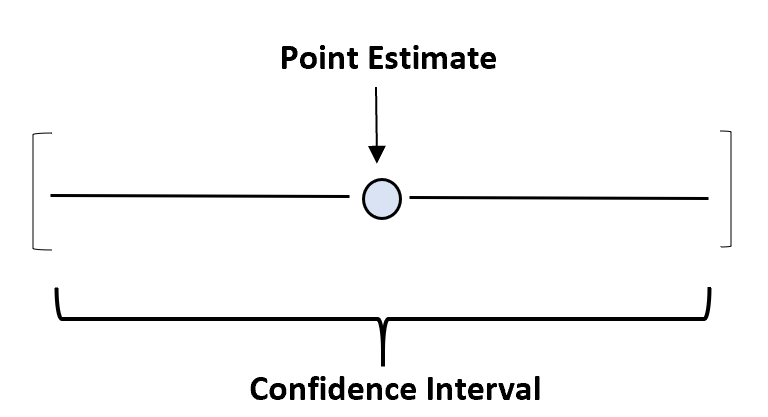
Beispielsweise können wir unseren Stichprobendurchschnitt von 150,4 Pfund verwenden, um das wahre Durchschnittsgewicht einer Schildkrötenart abzuschätzen. Unser Konfidenzintervall wäre dann ein Wertebereich – vielleicht 145 Pfund bis 155,8 Pfund.
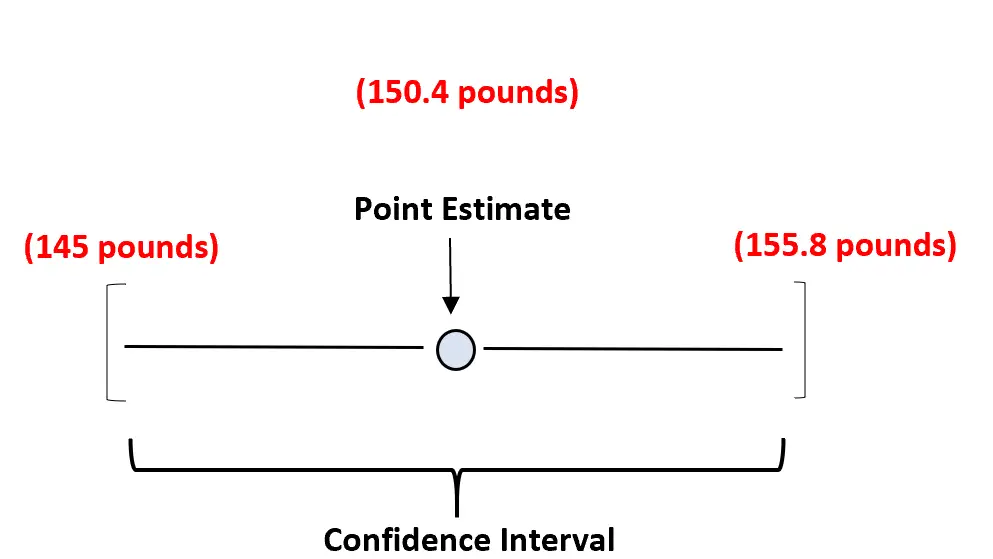
Unsere Punktschätzung ist unsere beste Schätzung des wahren Durchschnittsgewichts der Bevölkerung, und das Konfidenzintervall liefert einen Wertebereich, der wahrscheinlich das wahre Durchschnittsgewicht der Bevölkerung enthält.
Weitere Informationen zu Konfidenzintervallen finden Sie hier .
Zusätzliche Ressourcen
Statistik vs. Parameter: Was ist der Unterschied?
Bevölkerung vs. Beispiel: Was ist der Unterschied?
Eine Einführung in Konfidenzintervalle