So erstellen sie eine korrelationsmatrix in python
Eine Möglichkeit, die Beziehung zwischen zwei Variablen zu quantifizieren, ist die Verwendung des Pearson-Korrelationskoeffizienten , der ein Maß für den linearen Zusammenhang zwischen zwei Variablen ist .
Es nimmt einen Wert zwischen -1 und 1 an, wobei:
- -1 zeigt eine vollkommen negative lineare Korrelation an.
- 0 bedeutet keine lineare Korrelation.
- 1 zeigt eine vollkommen positive lineare Korrelation an.
Je weiter der Korrelationskoeffizient von Null entfernt ist, desto stärker ist die Beziehung zwischen den beiden Variablen.
In manchen Fällen möchten wir jedoch die Korrelation zwischen mehreren Variablenpaaren verstehen. In diesen Fällen können wir eine Korrelationsmatrix erstellen, bei der es sich um eine quadratische Tabelle handelt, die die Korrelationskoeffizienten zwischen mehreren paarweisen Kombinationen von Variablen zeigt.
In diesem Tutorial wird erläutert, wie Sie eine Korrelationsmatrix in Python erstellen und interpretieren.
So erstellen Sie eine Korrelationsmatrix in Python
Führen Sie die folgenden Schritte aus, um eine Korrelationsmatrix in Python zu erstellen.
Schritt 1: Erstellen Sie den Datensatz.
import pandas as pd data = {'assists': [4, 5, 5, 6, 7, 8, 8, 10], 'rebounds': [12, 14, 13, 7, 8, 8, 9, 13], 'points': [22, 24, 26, 26, 29, 32, 20, 14] } df = pd. DataFrame (data, columns=['assists','rebounds','points']) df assist rebound points 0 4 12 22 1 5 14 24 2 5 13 26 3 6 7 26 4 7 8 29 5 8 8 32 6 8 9 20 7 10 13 14
Schritt 2: Erstellen Sie die Korrelationsmatrix.
#create correlation matrix df. corr () assists rebound points assists 1.000000 -0.244861 -0.329573 rebounds -0.244861 1.000000 -0.522092 points -0.329573 -0.522092 1.000000 #create same correlation matrix with coefficients rounded to 3 decimals df. corr (). round (3) assists rebound points assists 1.000 -0.245 -0.330 rebounds -0.245 1.000 -0.522 points -0.330 -0.522 1.000
Schritt 3: Interpretieren Sie die Korrelationsmatrix.
Die Korrelationskoeffizienten entlang der Diagonalen der Tabelle sind alle gleich 1, da jede Variable perfekt mit sich selbst korreliert.
Alle anderen Korrelationskoeffizienten geben die Korrelation zwischen verschiedenen paarweisen Kombinationen von Variablen an. Zum Beispiel:
- Der Korrelationskoeffizient zwischen Assists und Rebounds beträgt -0,245 .
- Der Korrelationskoeffizient zwischen Assists und Punkten beträgt -0,330 .
- Der Korrelationskoeffizient zwischen Rebounds und Punkten beträgt -0,522 .
Schritt 4: Visualisieren Sie die Korrelationsmatrix (optional).
Sie können die Korrelationsmatrix mithilfe der in Pandas verfügbaren Stiloptionen visualisieren:
corr = df. corr () corr. style . background_gradient (cmap='coolwarm')
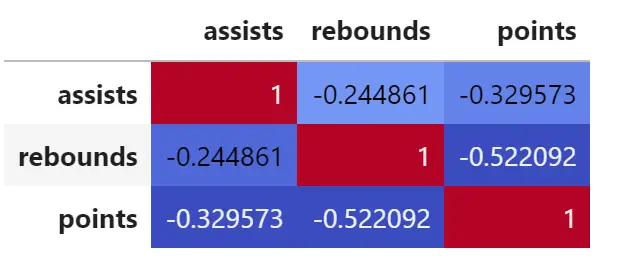
Sie können auch das Argument cmap ändern, um eine Korrelationsmatrix mit verschiedenen Farben zu erstellen.
corr = df. corr () corr. style . background_gradient (cmap=' RdYlGn ')
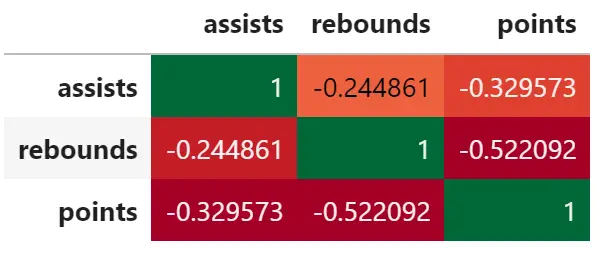
corr = df. corr () corr. style . background_gradient (cmap=' bwr ')
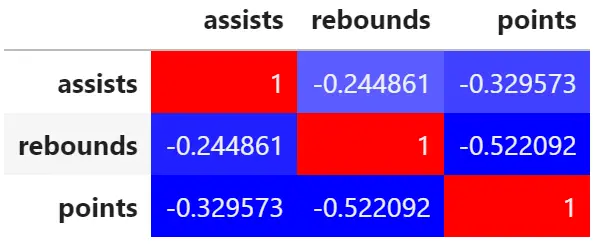
corr = df. corr () corr. style . background_gradient (cmap=' PuOr ')

Hinweis : Eine vollständige Liste der cmap- Argumente finden Sie in der Matplotlib-Dokumentation .