Kurvenanpassung in python (mit beispielen)

Häufig möchten Sie möglicherweise eine Kurve an einen Datensatz in Python anpassen.

Das folgende Schritt-für-Schritt-Beispiel erklärt, wie man in Python mit der Funktion numpy.polyfit() Kurven an Daten anpasst und wie man ermittelt, welche Kurve am besten zu den Daten passt.

Schritt 1: Daten erstellen und visualisieren

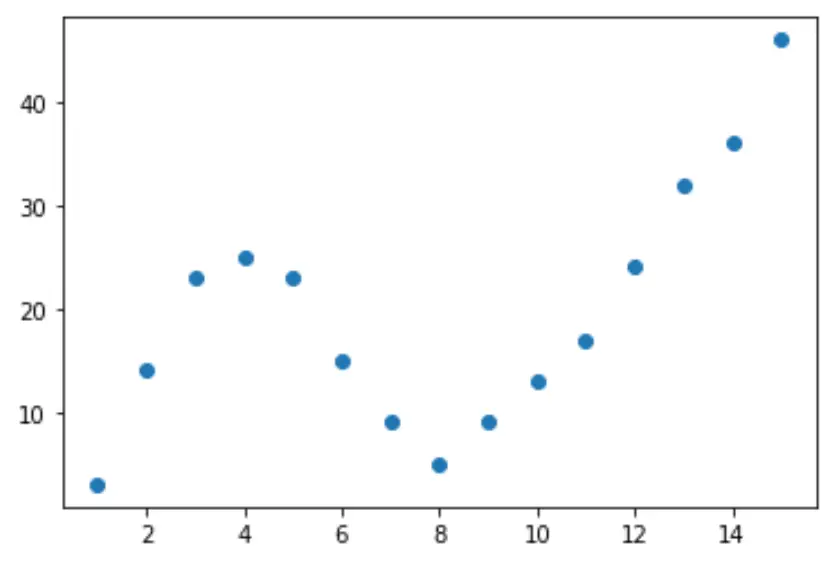
Beginnen wir mit der Erstellung eines gefälschten Datensatzes und erstellen dann ein Streudiagramm, um die Daten zu visualisieren:

 import pandas as pd
import matplotlib. pyplot as plt

#createDataFrame
df = pd. DataFrame ({' x ': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15],
                   ' y ': [3, 14, 23, 25, 23, 15, 9, 5, 9, 13, 17, 24, 32, 36, 46]})

#create scatterplot of x vs. y
plt. scatter (df. x , df. y ) 

Schritt 2: Passen Sie mehrere Kurven an

Passen wir dann mehrere polynomiale Regressionsmodelle an die Daten an und visualisieren die Kurve jedes Modells im selben Diagramm:

 import numpy as np

#fit polynomial models up to degree 5
model1 = np. poly1d (np. polyfit (df. x , df. y , 1))
model2 = np. poly1d (np. polyfit (df. x , df. y , 2))
model3 = np. poly1d (np. polyfit (df. x , df. y , 3))
model4 = np. poly1d (np. polyfit (df. x , df. y , 4))
model5 = np. poly1d (np. polyfit (df. x , df. y , 5))

#create scatterplot
polyline = np. linspace (1, 15, 50)
plt. scatter (df. x , df. y )

#add fitted polynomial lines to scatterplot 
plt. plot (polyline, model1(polyline), color=' green ')
plt. plot (polyline, model2(polyline), color=' red ')
plt. plot (polyline, model3(polyline), color=' purple ')
plt. plot (polyline, model4(polyline), color=' blue ')
plt. plot (polyline, model5(polyline), color=' orange ')
plt. show ()

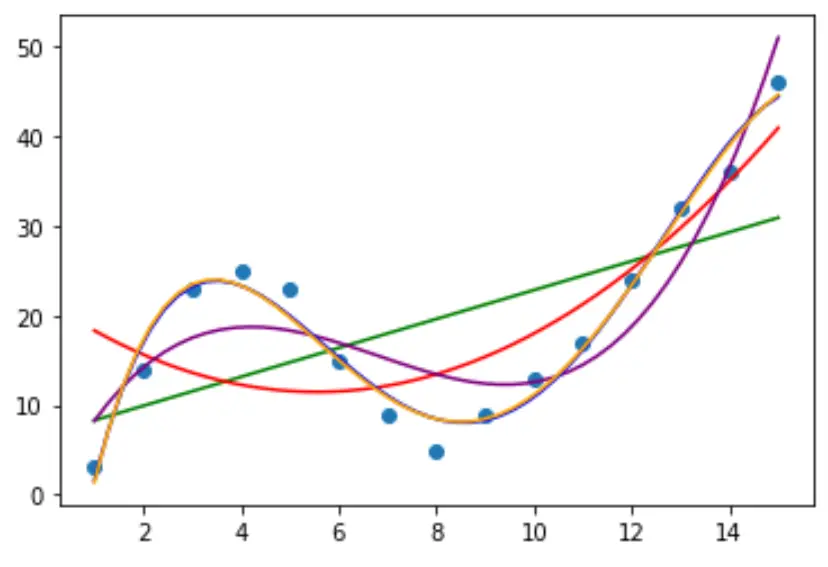
Um zu bestimmen, welche Kurve am besten zu den Daten passt, können wir uns das angepasste R-Quadrat jedes Modells ansehen.

Dieser Wert gibt uns den Prozentsatz der Variation in der Antwortvariablen an, der durch die Prädiktorvariablen im Modell erklärt werden kann, angepasst an die Anzahl der Prädiktorvariablen.

 #define function to calculate adjusted r-squared
def adjR(x, y, degree):
    results = {}
    coeffs = np. polyfit (x, y, degree)
    p = np. poly1d (coeffs)
    yhat = p(x)
    ybar = np. sum (y)/len(y)
    ssreg = np. sum ((yhat-ybar)**2)
    sstot = np. sum ((y - ybar)**2)
    results[' r_squared '] = 1- (((1-(ssreg/sstot))*(len(y)-1))/(len(y)-degree-1))

    return results

#calculated adjusted R-squared of each model
adjR(df. x , df. y , 1)
adjR(df. x , df. y , 2)
adjR(df. x , df. y , 3)
adjR(df. x , df. y , 4)
adjR(df. x , df. y , 5)

{'r_squared': 0.3144819}
{'r_squared': 0.5186706}
{'r_squared': 0.7842864}
{'r_squared': 0.9590276}
{'r_squared': 0.9549709}

Aus dem Ergebnis können wir ersehen, dass das Modell mit dem höchsten angepassten R-Quadrat das Polynom vierten Grades ist, das einen angepassten R-Quadrat von 0,959 aufweist.

Schritt 3: Visualisieren Sie die endgültige Kurve

Schließlich können wir ein Streudiagramm mit der Kurve des Polynommodells vierten Grades erstellen:

 #fit fourth-degree polynomial
model4 = np. poly1d (np. polyfit (df. x , df. y , 4))

#define scatterplot
polyline = np. linspace (1, 15, 50)
plt. scatter (df. x , df. y )

#add fitted polynomial curve to scatterplot
plt. plot (polyline, model4(polyline), ' -- ', color=' red ')
plt. show ()

Wir können die Gleichung für diese Zeile auch mit der Funktion print() erhalten:

 print (model4)

          4 3 2
-0.01924x + 0.7081x - 8.365x + 35.82x - 26.52

Die Gleichung der Kurve lautet wie folgt:

y = -0,01924x ⁴ + 0,7081x ³ – 8,365x ² + 35,82x – 26,52

Wir können diese Gleichung verwenden, um den Wert der Antwortvariablen basierend auf den Prädiktorvariablen im Modell vorherzusagen. Wenn zum Beispiel x = 4, dann würden wir y = 23,32 vorhersagen:

y = -0,0192(4) ⁴ + 0,7081(4) ³ – 8,365(4) ² + 35,82(4) – 26,52 = 23,32

Zusätzliche Ressourcen

Eine Einführung in die Polynomregression
So führen Sie eine Polynomregression in Python durch