So testen sie die normalität in python (4 methoden)

Viele statistische Tests gehen davon aus , dass Datensätze normalverteilt sind.

Es gibt vier gängige Methoden, diese Hypothese in Python zu überprüfen:

1. (Visuelle Methode) Erstellen Sie ein Histogramm.

• Wenn das Histogramm annähernd „glockenförmig“ ist, wird davon ausgegangen, dass die Daten normalverteilt sind.

2. (Visuelle Methode) Erstellen Sie ein QQ-Diagramm.

• Wenn die Punkte im Diagramm ungefähr auf einer geraden diagonalen Linie liegen, wird davon ausgegangen, dass die Daten normalverteilt sind.

3. (Formeller statistischer Test) Führen Sie einen Shapiro-Wilk-Test durch.

• Wenn der p-Wert des Tests größer als α = 0,05 ist, wird davon ausgegangen, dass die Daten normalverteilt sind.

4. (Formeller statistischer Test) Führen Sie einen Kolmogorov-Smirnov-Test durch.

• Wenn der p-Wert des Tests größer als α = 0,05 ist, wird davon ausgegangen, dass die Daten normalverteilt sind.

Die folgenden Beispiele zeigen, wie jede dieser Methoden in der Praxis angewendet werden kann.

Methode 1: Erstellen Sie ein Histogramm

Der folgende Code zeigt, wie man ein Histogramm für einen Datensatz erstellt, der einer logarithmischen Normalverteilung folgt:

 import math
import numpy as np
from scipy. stats import lognorm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create histogram to visualize values in dataset
plt. hist (lognorm_dataset, edgecolor=' black ', bins=20) 

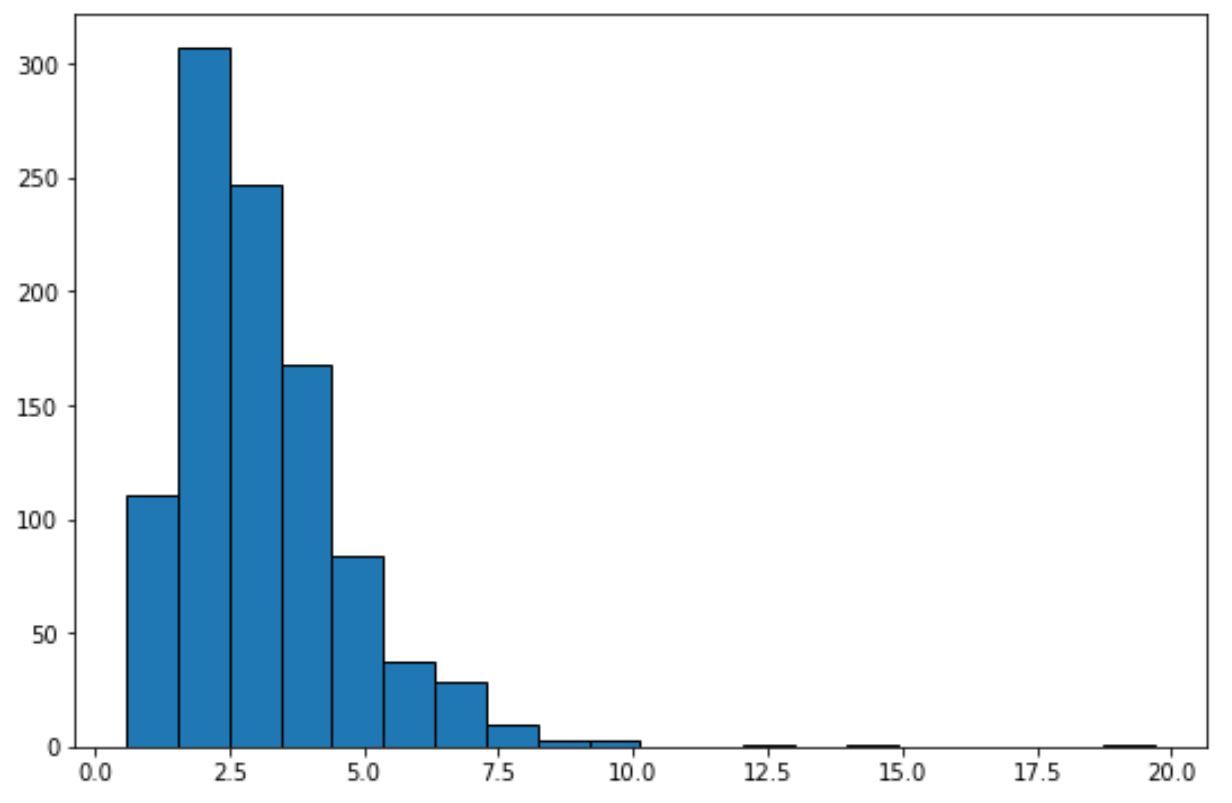
Wenn wir uns dieses Histogramm ansehen, können wir erkennen, dass der Datensatz keine „Glockenform“ aufweist und nicht normalverteilt ist.

Methode 2: Erstellen Sie ein QQ-Diagramm

Der folgende Code zeigt, wie ein QQ-Diagramm für einen Datensatz erstellt wird, der einer logarithmischen Normalverteilung folgt:

 import math
import numpy as np
from scipy. stats import lognorm
import statsmodels. api as sm
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#create QQ plot with 45-degree line added to plot
fig = sm. qqplot (lognorm_dataset, line=' 45 ')

plt. show ()

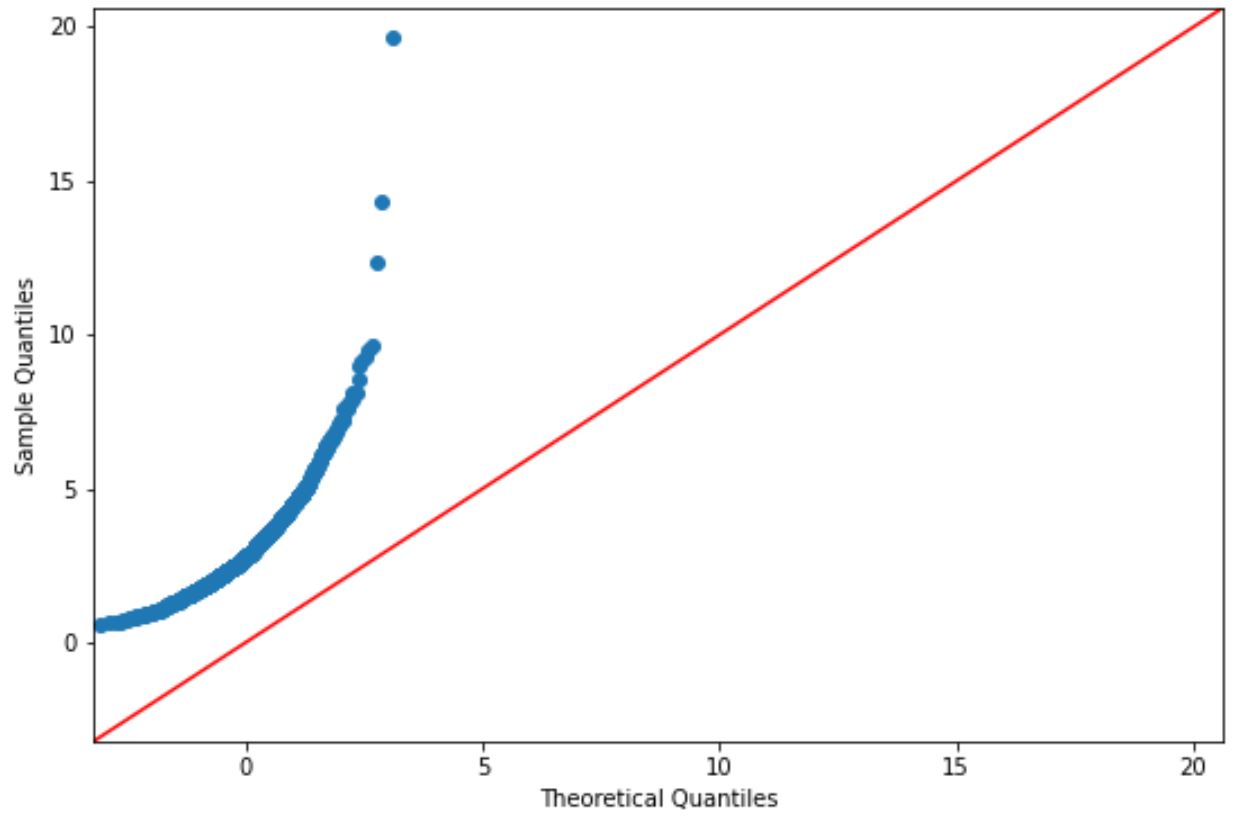
Liegen die Plotpunkte ungefähr auf einer geraden Diagonale, gehen wir im Allgemeinen davon aus, dass ein Datensatz normalverteilt ist.

Allerdings entsprechen die Punkte in diesem Diagramm eindeutig nicht der roten Linie, sodass wir nicht davon ausgehen können, dass dieser Datensatz normalverteilt ist.

Dies sollte sinnvoll sein, da wir die Daten mithilfe einer logarithmischen Normalverteilungsfunktion generiert haben.

Methode 3: Führen Sie einen Shapiro-Wilk-Test durch

Der folgende Code zeigt, wie ein Shapiro-Wilk für einen Datensatz durchgeführt wird, der einer logarithmischen Normalverteilung folgt:

 import math
import numpy as np
from scipy.stats import shapiro 
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Shapiro-Wilk test for normality
shapiro(lognorm_dataset)

ShapiroResult(statistic=0.8573324680328369, pvalue=3.880663073872444e-29)

Aus dem Ergebnis können wir ersehen, dass die Teststatistik 0,857 beträgt und der entsprechende p-Wert 3,88e-29 beträgt (extrem nahe bei Null).

Da der p-Wert kleiner als 0,05 ist, lehnen wir die Nullhypothese des Shapiro-Wilk-Tests ab.

Das bedeutet, dass wir genügend Beweise dafür haben, dass die Stichprobendaten nicht aus einer Normalverteilung stammen.

Methode 4: Führen Sie einen Kolmogorov-Smirnov-Test durch

Der folgende Code zeigt, wie ein Kolmogorov-Smirnov-Test für einen Datensatz durchgeführt wird, der einer logarithmischen Normalverteilung folgt:

 import math
import numpy as np
from scipy.stats import kstest
from scipy. stats import lognorm

#make this example reproducible
n.p. random . seeds (1)

#generate dataset that contains 1000 log-normal distributed values
lognorm_dataset = lognorm. rvs (s=.5, scale= math.exp (1), size=1000)

#perform Kolmogorov-Smirnov test for normality
kstest(lognorm_dataset, ' norm ')

KstestResult(statistic=0.84125708308077, pvalue=0.0)

Aus dem Ergebnis können wir ersehen, dass die Teststatistik 0,841 beträgt und der entsprechende p-Wert 0,0 beträgt.

Da der p-Wert kleiner als 0,05 ist, lehnen wir die Nullhypothese des Kolmogorov-Smirnov-Tests ab.

Das bedeutet, dass wir genügend Beweise dafür haben, dass die Stichprobendaten nicht aus einer Normalverteilung stammen.

Umgang mit nicht normalen Daten

Wenn ein bestimmter Datensatz nicht normalverteilt ist , können wir häufig eine der folgenden Transformationen durchführen, um ihn normaler zu verteilen:

1. Log-Transformation: x-Werte in log(x) umwandeln.

2. Quadratwurzeltransformation: Transformieren Sie die Werte von x in √x .

3. Kubikwurzeltransformation: Transformieren Sie die Werte von x in x ^1/3 .

Durch die Durchführung dieser Transformationen wird der Datensatz im Allgemeinen normaler verteilt.

Lesen Sie dieses Tutorial, um zu erfahren, wie Sie diese Transformationen in Python durchführen.