So führen sie eine quadratische regression in r durch
Wenn zwei Variablen eine lineare Beziehung haben, können wir oft eine einfache lineare Regression verwenden, um ihre Beziehung zu quantifizieren.

Wenn jedoch zwei Variablen in einer quadratischen Beziehung stehen, können wir die quadratische Regression verwenden, um ihre Beziehung zu quantifizieren.

In diesem Tutorial wird erklärt, wie man eine quadratische Regression in R durchführt.
Beispiel: Quadratische Regression in R
Angenommen, wir möchten den Zusammenhang zwischen der Anzahl der geleisteten Arbeitsstunden und der gemeldeten Zufriedenheit verstehen. Wir haben die folgenden Daten zur Anzahl der pro Woche geleisteten Arbeitsstunden und zum gemeldeten Grad der Zufriedenheit (auf einer Skala von 0 bis 100) für 11 verschiedene Personen:

Führen Sie die folgenden Schritte aus, um ein quadratisches Regressionsmodell in R anzupassen.
Schritt 1: Geben Sie die Daten ein.
Zuerst erstellen wir einen Datenrahmen, der unsere Daten enthält:
#createdata data <- data.frame(hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60), happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27)) #viewdata data hours happiness 1 6 14 2 9 28 3 12 50 4 14 70 5 30 89 6 35 94 7 40 90 8 47 75 9 51 59 10 55 44 11 60 27
Schritt 2: Visualisieren Sie die Daten.
Als Nächstes erstellen wir ein einfaches Streudiagramm zur Visualisierung der Daten.
#create scatterplot
plot(data$hours, data$happiness, pch=16)
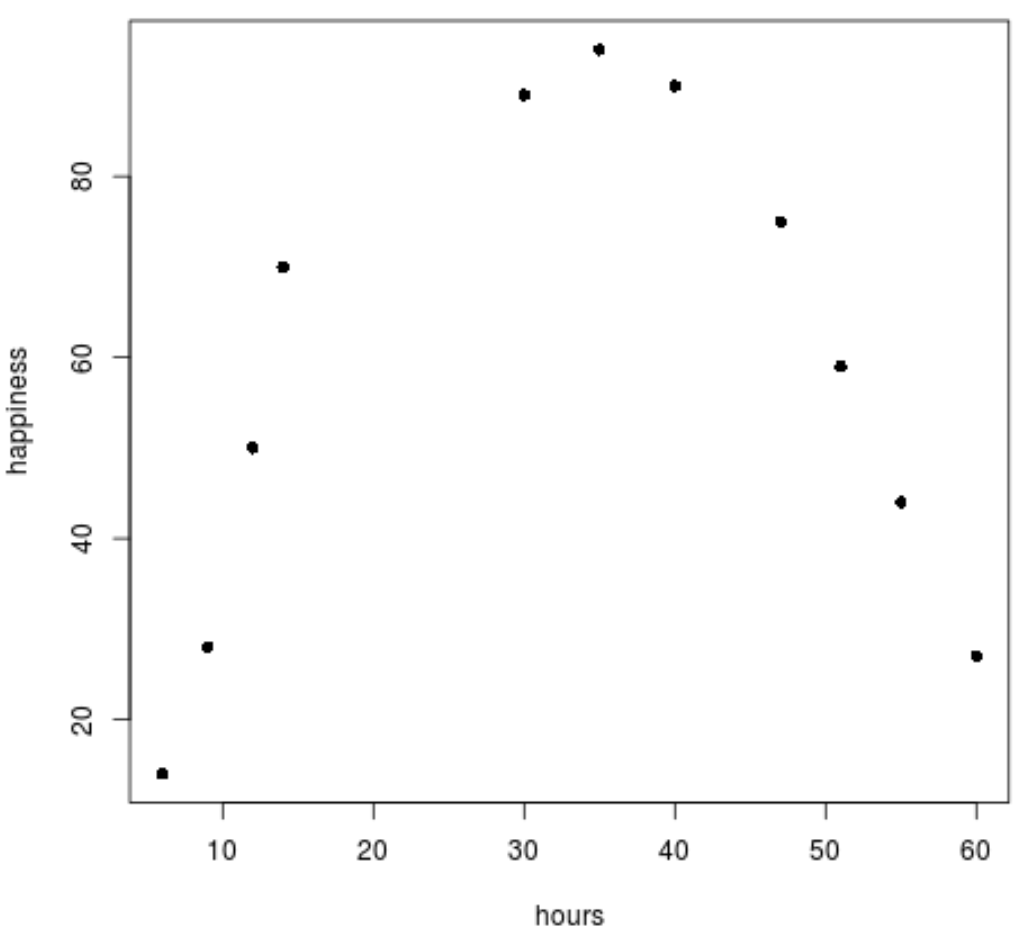
Wir können deutlich erkennen, dass die Daten keinem linearen Muster folgen.
Schritt 3: Passen Sie ein einfaches lineares Regressionsmodell an.
Als Nächstes passen wir ein einfaches lineares Regressionsmodell an, um zu sehen, wie gut es zu den Daten passt:
#fit linear model linearModel <- lm(happiness ~ hours, data=data) #view model summary summary(linearModel) Call: lm(formula = happiness ~ hours) Residuals: Min 1Q Median 3Q Max -39.34 -21.99 -2.03 23.50 35.11 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 48.4531 17.3288 2.796 0.0208 * hours 0.2981 0.4599 0.648 0.5331 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 28.72 on 9 degrees of freedom Multiple R-squared: 0.0446, Adjusted R-squared: -0.06156 F-statistic: 0.4201 on 1 and 9 DF, p-value: 0.5331
Die durch das Modell erklärte Gesamtvarianz des Glücks beträgt nur 4,46 % , wie der multiple R-Quadrat-Wert zeigt.
Schritt 4: Passen Sie ein quadratisches Regressionsmodell an.
Als nächstes passen wir ein quadratisches Regressionsmodell an.
#create a new variable for hours 2 data$hours2 <- data$hours^2 #fit quadratic regression model quadraticModel <- lm(happiness ~ hours + hours2, data=data) #view model summary summary(quadraticModel) Call: lm(formula = happiness ~ hours + hours2, data = data) Residuals: Min 1Q Median 3Q Max -6.2484 -3.7429 -0.1812 1.1464 13.6678 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -18.25364 6.18507 -2.951 0.0184 * hours 6.74436 0.48551 13.891 6.98e-07 *** hours2 -0.10120 0.00746 -13.565 8.38e-07 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 6.218 on 8 degrees of freedom Multiple R-squared: 0.9602, Adjusted R-squared: 0.9502 F-statistic: 96.49 on 2 and 8 DF, p-value: 2.51e-06
Die durch das Modell erklärte Gesamtvarianz des Glücks stieg auf 96,02 % .
Mit dem folgenden Code können wir visualisieren, wie gut das Modell zu den Daten passt:
#create sequence of hour values hourValues <- seq(0, 60, 0.1) #create list of predicted happiness levels using quadratic model happinessPredict <- predict(quadraticModel, list(hours=hourValues, hours2=hourValues^2)) #create scatterplot of original data values plot(data$hours, data$happiness, pch=16) #add predicted lines based on quadratic regression model lines(hourValues, happinessPredict, col='blue')
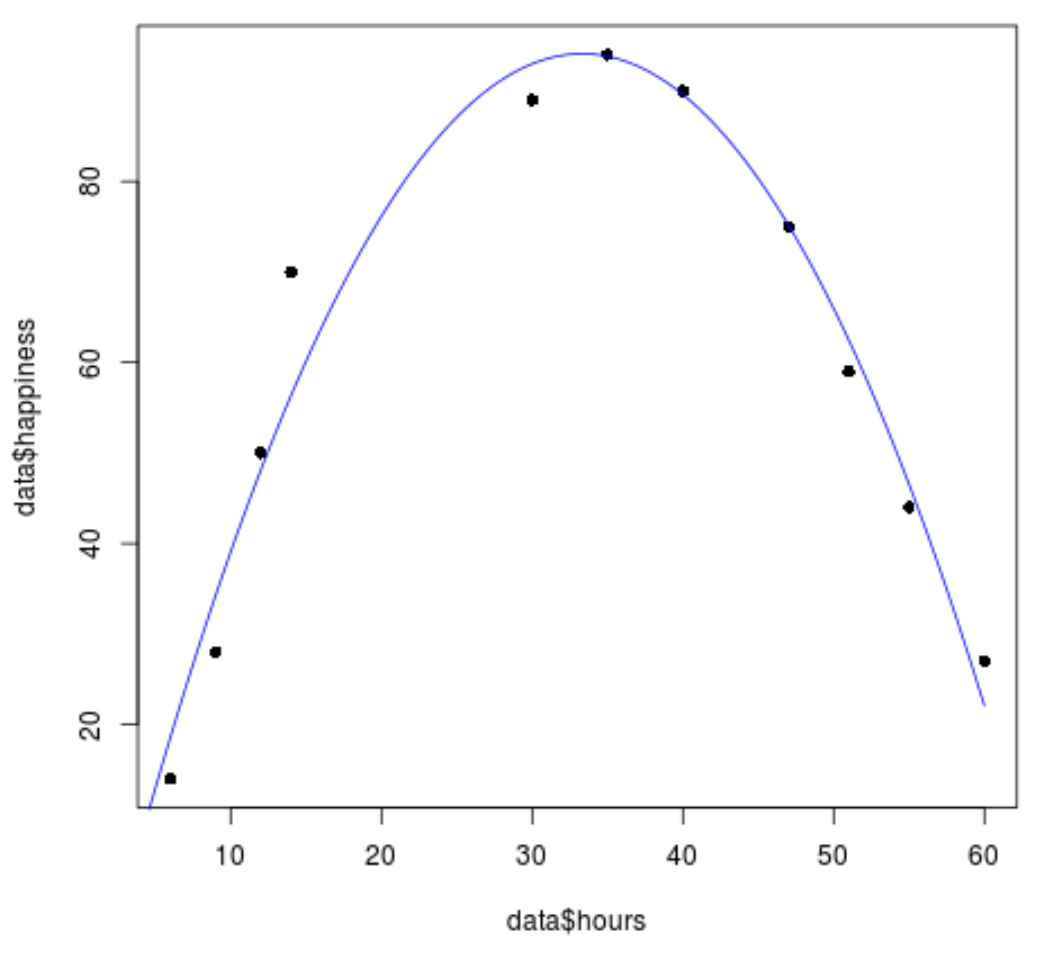
Wir können sehen, dass die quadratische Regressionslinie recht gut zu den Datenwerten passt.
Schritt 5: Interpretieren Sie das quadratische Regressionsmodell.
Im vorherigen Schritt haben wir gesehen, dass das Ergebnis des quadratischen Regressionsmodells war:
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -18.25364 6.18507 -2.951 0.0184 *
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***
Basierend auf den hier dargestellten Koeffizienten wäre die angepasste quadratische Regression:
Glück = -0,1012 (Stunden) 2 + 6,7444 (Stunden) – 18,2536
Mit dieser Gleichung können wir das prognostizierte Glück einer Person anhand der Anzahl der Stunden, die sie pro Woche arbeitet, ermitteln.
Beispielsweise hätte eine Person, die 60 Stunden pro Woche arbeitet, einen Glücksgrad von 22,09 :
Glück = -0,1012(60) 2 + 6,7444(60) – 18,2536 = 22,09
Umgekehrt sollte eine Person, die 30 Stunden pro Woche arbeitet, einen Glücksgrad von 92,99 haben:
Glück = -0,1012(30) 2 + 6,7444(30) – 18,2536 = 92,99