So führen sie eine quadratische regression in stata durch

Wenn zwei Variablen in einer linearen Beziehung stehen, können Sie häufig eine einfache lineare Regression verwenden, um ihre Beziehung zu quantifizieren.

Wenn jedoch zwei Variablen in einer quadratischen Beziehung stehen, können Sie die quadratische Regression verwenden, um ihre Beziehung zu quantifizieren.

In diesem Tutorial wird erklärt, wie man eine quadratische Regression in Stata durchführt.

Beispiel: Quadratische Regression in Stata

Angenommen, wir möchten den Zusammenhang zwischen der Anzahl der geleisteten Arbeitsstunden und dem Glück verstehen. Wir haben die folgenden Daten zur Anzahl der pro Woche geleisteten Arbeitsstunden und zum gemeldeten Grad der Zufriedenheit (auf einer Skala von 0 bis 100) für 16 verschiedene Personen:

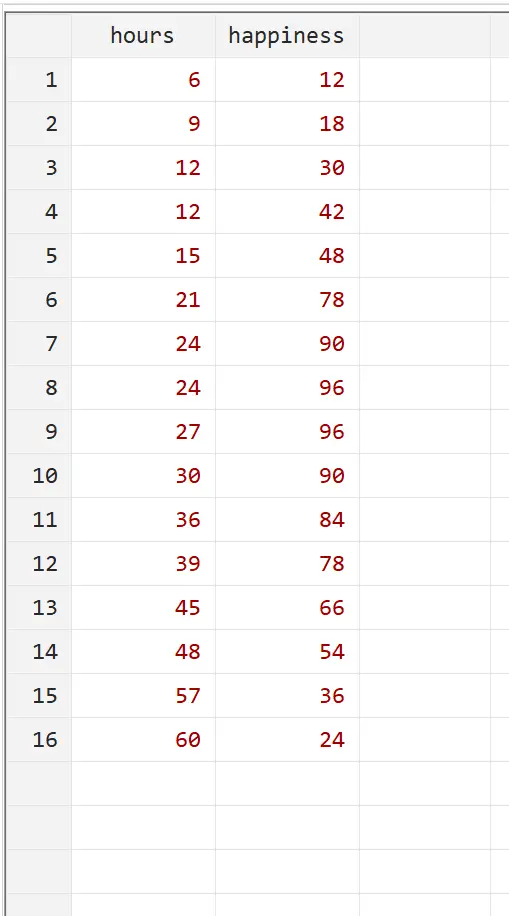
Sie können dieses Beispiel reproduzieren, indem Sie im oberen Menü über Daten > Dateneditor > Dateneditor (Bearbeiten) genau diese Daten in Stata eingeben.

Führen Sie die folgenden Schritte aus, um eine quadratische Regression in Stata durchzuführen.

Schritt 1: Visualisieren Sie die Daten.

Bevor wir die quadratische Regression verwenden können, müssen wir sicherstellen, dass die Beziehung zwischen der erklärenden Variablen (Stunden) und der Antwortvariablen (Glück) tatsächlich quadratisch ist. Lassen Sie uns die Daten mithilfe eines Streudiagramms visualisieren , indem wir Folgendes in das Befehlsfeld eingeben:

zerstreue die Stunden des Glücks

Dadurch entsteht das folgende Streudiagramm:

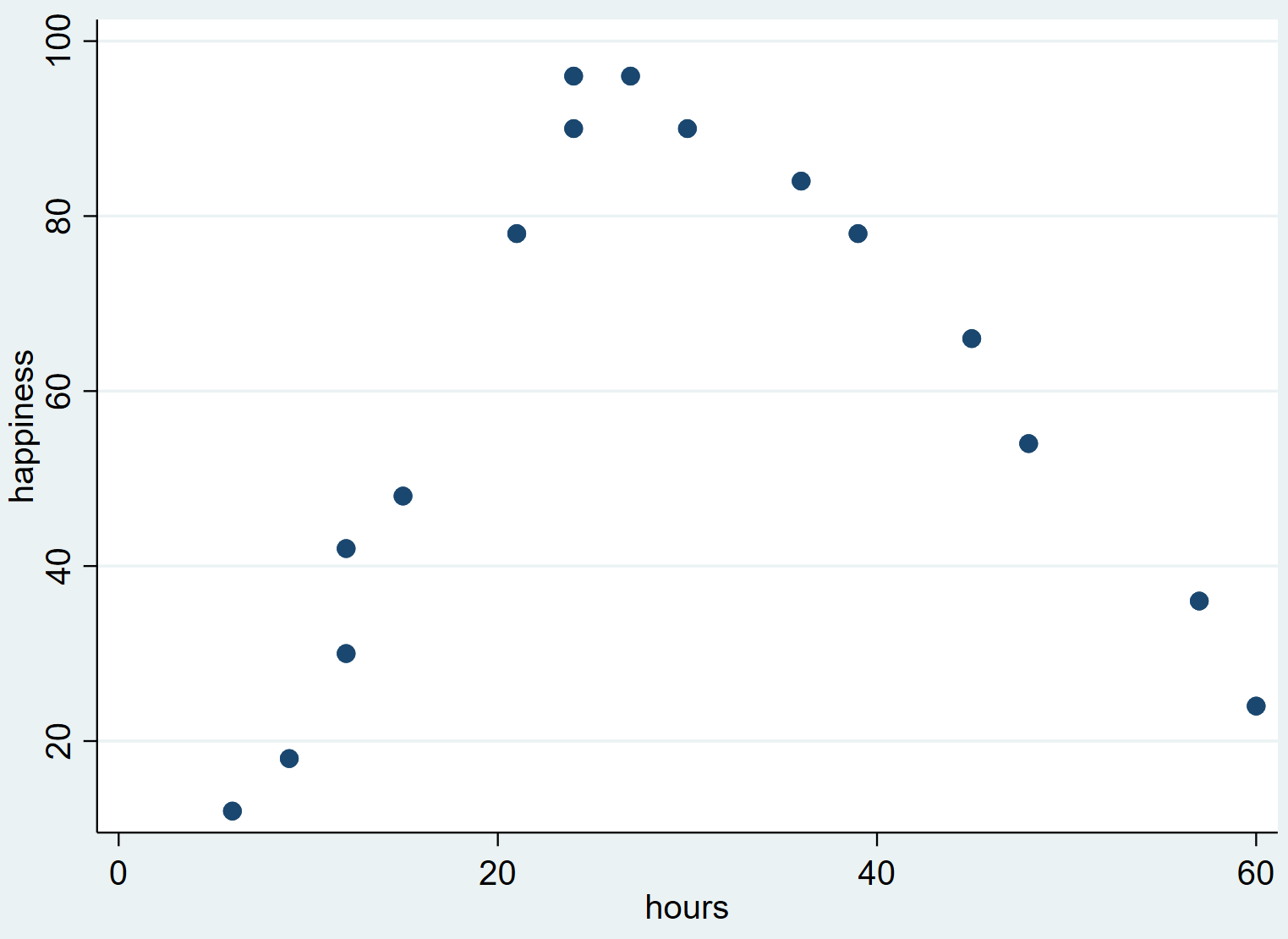
Wir können sehen, dass das Glück tendenziell zunimmt, wenn die Anzahl der geleisteten Arbeitsstunden von Null auf einen bestimmten Punkt ansteigt, dann aber zu sinken beginnt, wenn die Anzahl der geleisteten Arbeitsstunden etwa 30 übersteigt.

Diese umgekehrte „U“-Form im Streudiagramm weist darauf hin, dass zwischen geleisteten Arbeitsstunden und Glück ein quadratischer Zusammenhang besteht, was bedeutet, dass wir zur Quantifizierung dieses Zusammenhangs eine quadratische Regression verwenden sollten.

Schritt 2: Führen Sie eine quadratische Regression durch.

Bevor wir das quadratische Regressionsmodell an die Daten anpassen, müssen wir eine neue Variable für die quadrierten Werte unserer Stunden- Prädiktorvariablen erstellen. Wir können dies tun, indem wir Folgendes in das Befehlsfeld eingeben:

Genstunden2 = Stunden*Stunden

Wir können diese neue Variable anzeigen, indem wir im oberen Menü zu Daten > Dateneditor > Dateneditor (Durchsuchen) gehen.

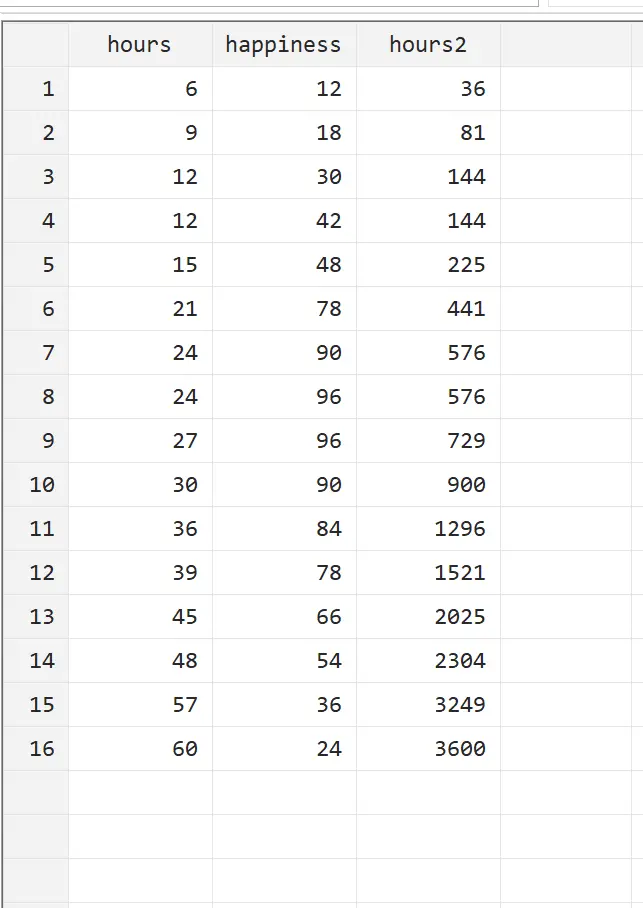
Wir können sehen, dass Stunden2 einfach Stunden im Quadrat sind. Wir können nun eine quadratische Regression durchführen, indem wir Stunden und Stunden2 als erklärende Variablen und Glück als Antwortvariable verwenden. Um eine quadratische Regression durchzuführen, geben Sie Folgendes in das Befehlsfeld ein:

Rückschritt Stunden des Glücks Stunden2

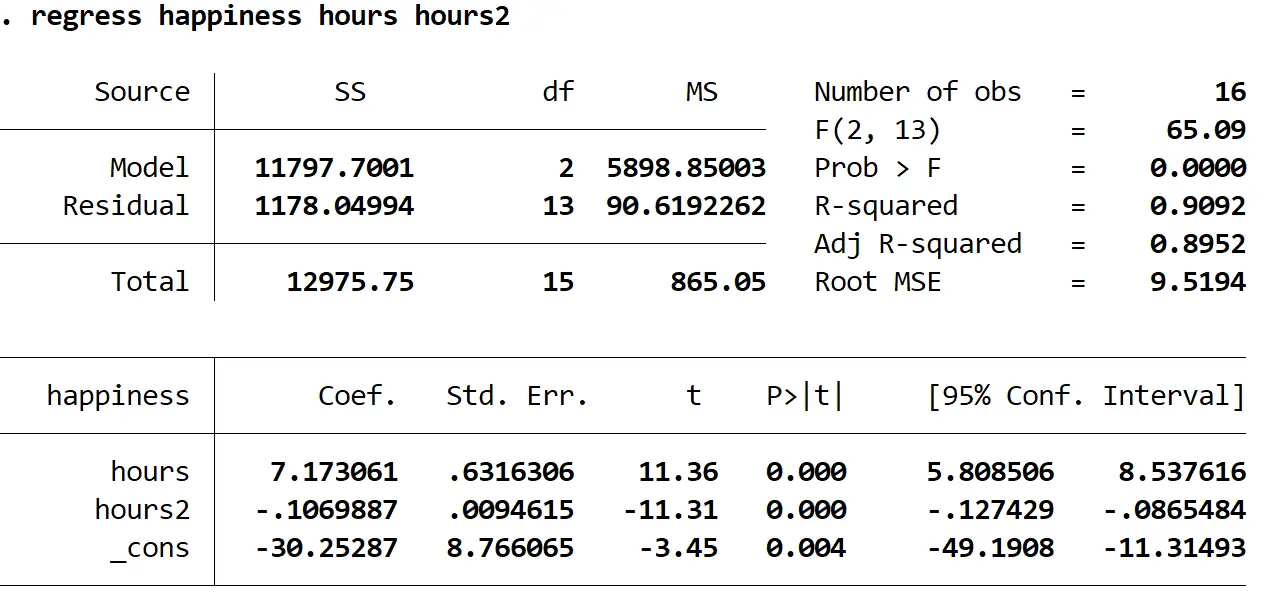
So interpretieren Sie die interessantesten Zahlen im Ergebnis:

Wahrscheinlich > F: 0,000. Dies ist der p-Wert für die Gesamtregression. Da dieser Wert kleiner als 0,05 ist, bedeutet dies, dass die Prädiktorvariablen Stunden und Stunden ² zusammen einen statistisch signifikanten Zusammenhang mit der Antwortvariablen Glück haben.

R im Quadrat: 0,9092. Dies ist der Anteil der Varianz der Antwortvariablen, der durch die erklärende Variable erklärt werden kann. In diesem Beispiel können 90,92 % der Glücksschwankungen durch Stunden und Stunden erklärt werden ² .

Regressionsgleichung: Mithilfe der in der Ausgabetabelle angezeigten Koeffizientenwerte können wir eine Regressionsgleichung erstellen. In diesem Fall wäre die Gleichung:

vorhergesagtes Glück = -30,25287 + 7,173061 (Stunden) – 0,1069887 ( ² Stunden)

Mit dieser Gleichung können wir das prognostizierte Glück einer Person anhand der Anzahl der Stunden, die sie pro Woche arbeitet, ermitteln.

Beispielsweise sollte eine Person, die 60 Stunden pro Woche arbeitet, einen Glücksgrad von 14,97 haben:

vorhergesagtes Glück = -30,25287 + 7,173061(60) – .1069887(60 ² ) = 14,97 .

Umgekehrt sollte eine Person, die 30 Stunden pro Woche arbeitet, einen Glücksgrad von 88,65 haben:

vorhergesagtes Glück = -30,25287 + 7,173061(30) – .1069887(30 ² ) = 88,65 .

Schritt 3: Melden Sie die Ergebnisse.

Abschließend möchten wir die Ergebnisse unserer quadratischen Regression berichten. Hier ist ein Beispiel dafür:

Eine quadratische Regression wurde durchgeführt, um die Beziehung zwischen der Anzahl der Arbeitsstunden einer Person und ihrem entsprechenden Zufriedenheitsgrad (gemessen von 0 bis 100) zu quantifizieren. Für die Analyse wurde eine Stichprobe von 16 Personen herangezogen.

Die Ergebnisse zeigten, dass zwischen den erklärenden Variablen Stunden und Stunden ² und der Antwortvariablen Glück ein statistisch signifikanter Zusammenhang bestand (F(2, 13) = 65,09, p < 0,0001).

Zusammen machten diese beiden erklärenden Variablen 90,92 % der erklärten Variabilität des Glücks aus.

Es stellte sich heraus, dass die Regressionsgleichung lautete:

vorhergesagtes Glück = -30,25287 + 7,173061 (Stunden) – 0,1069887 ( ² Stunden)