So berechnen sie den root mean square error (rmse) in excel

In der Statistik ist die Regressionsanalyse eine Technik, die wir verwenden, um die Beziehung zwischen einer Prädiktorvariablen x und einer Antwortvariablen y zu verstehen.

Wenn wir eine Regressionsanalyse durchführen, erhalten wir ein Modell, das uns den vorhergesagten Wert der Antwortvariablen basierend auf dem Wert der Prädiktorvariablen mitteilt.

Eine Möglichkeit zu beurteilen, wie gut unser Modell zu einem bestimmten Datensatz passt, besteht darin, den mittleren quadratischen Fehler zu berechnen. Dabei handelt es sich um eine Metrik, die uns sagt, wie weit unsere vorhergesagten Werte im Durchschnitt von unseren beobachteten Werten entfernt sind.

Die Formel zum Ermitteln des mittleren quadratischen Fehlers, besser bekannt als RMSE , lautet:

RMSE = √[ Σ(P _i – O _i ) ² / n ]

Gold:

• Σ ist ein ausgefallenes Symbol, das „Summe“ bedeutet
• P _i ist der vorhergesagte Wert für die ^i-te Beobachtung im Datensatz
• O _i ist der beobachtete Wert für die ^i-te Beobachtung im Datensatz
• n ist die Stichprobengröße

Technische Hinweise :

• Der mittlere quadratische Fehler kann für jede Art von Modell berechnet werden, das vorhergesagte Werte erzeugt, die dann mit den beobachteten Werten eines Datensatzes verglichen werden können.
• Der mittlere quadratische Fehler wird manchmal auch als mittlere quadratische Abweichung bezeichnet, die oft als RMSD abgekürzt wird.

Schauen wir uns als Nächstes ein Beispiel für die Berechnung des mittleren quadratischen Fehlers in Excel an.

So berechnen Sie den mittleren quadratischen Fehler in Excel

Es gibt keine integrierte Funktion zur Berechnung des RMSE in Excel, aber wir können ihn ganz einfach mit einer einzigen Formel berechnen. Wir zeigen, wie man den RMSE für zwei verschiedene Szenarien berechnet.

Szenario 1

In einem Szenario können Sie eine Spalte mit den vorhergesagten Werten Ihres Modells und eine andere Spalte mit den beobachteten Werten haben. Das Bild unten zeigt ein Beispiel für dieses Szenario:

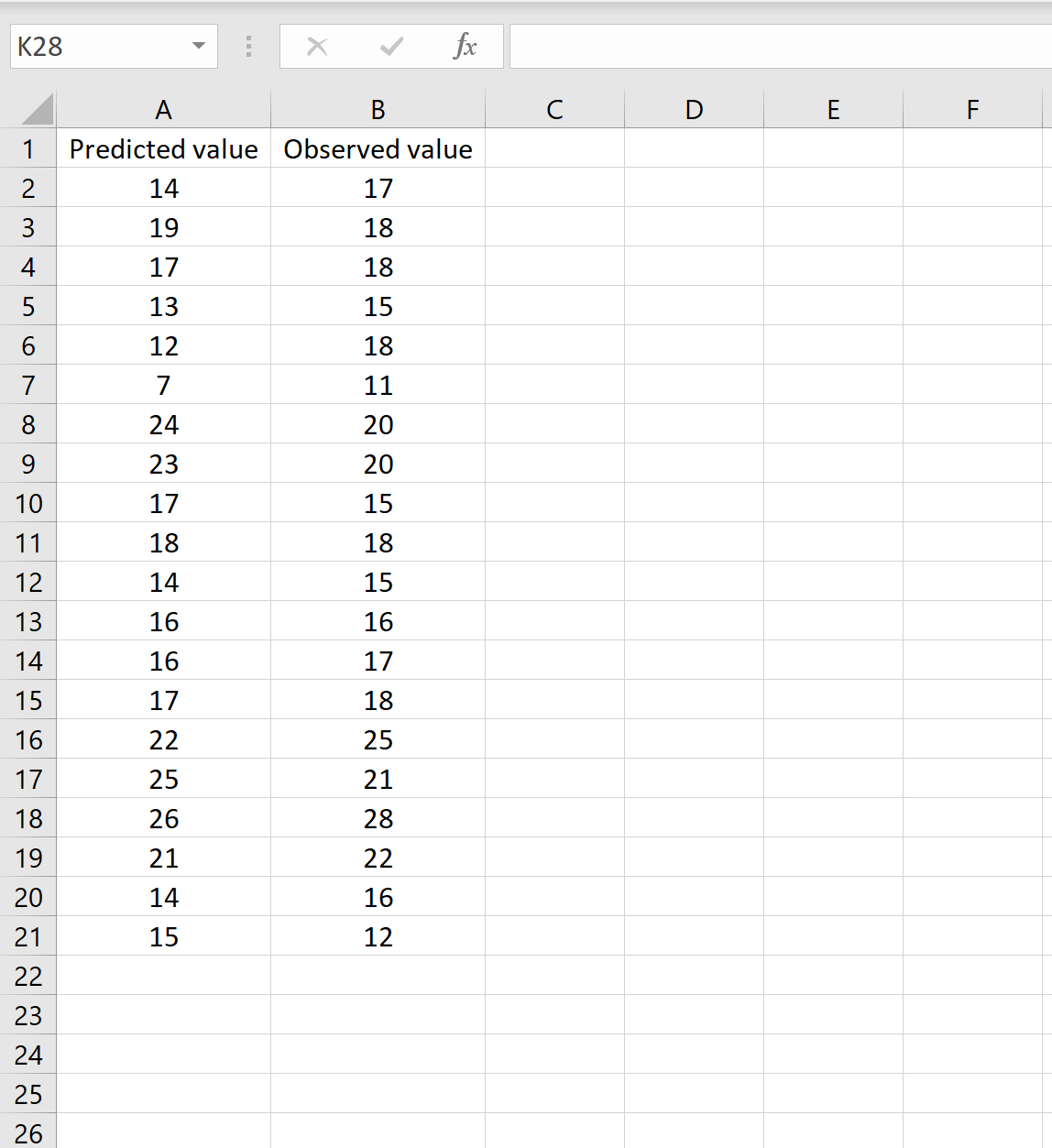
Wenn ja, können Sie den RMSE berechnen, indem Sie die folgende Formel in eine beliebige Zelle eingeben und dann auf STRG+UMSCHALT+EINGABETASTE klicken:

=SQRT(SUMSQ(A2:A21-B2:B21) / COUNT(A2:A21))

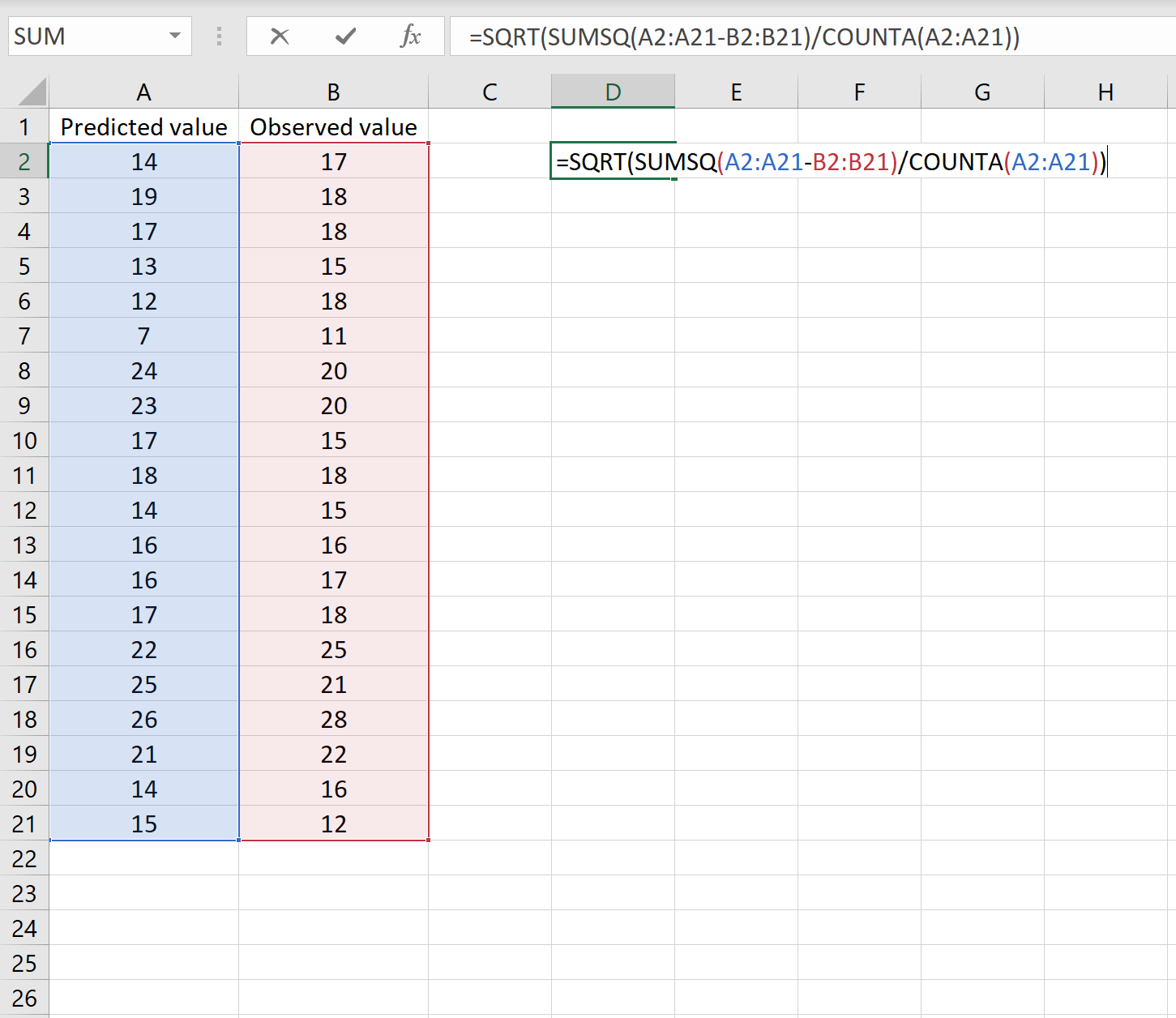
Dies sagt uns, dass der mittlere quadratische Fehler 2,6646 beträgt.

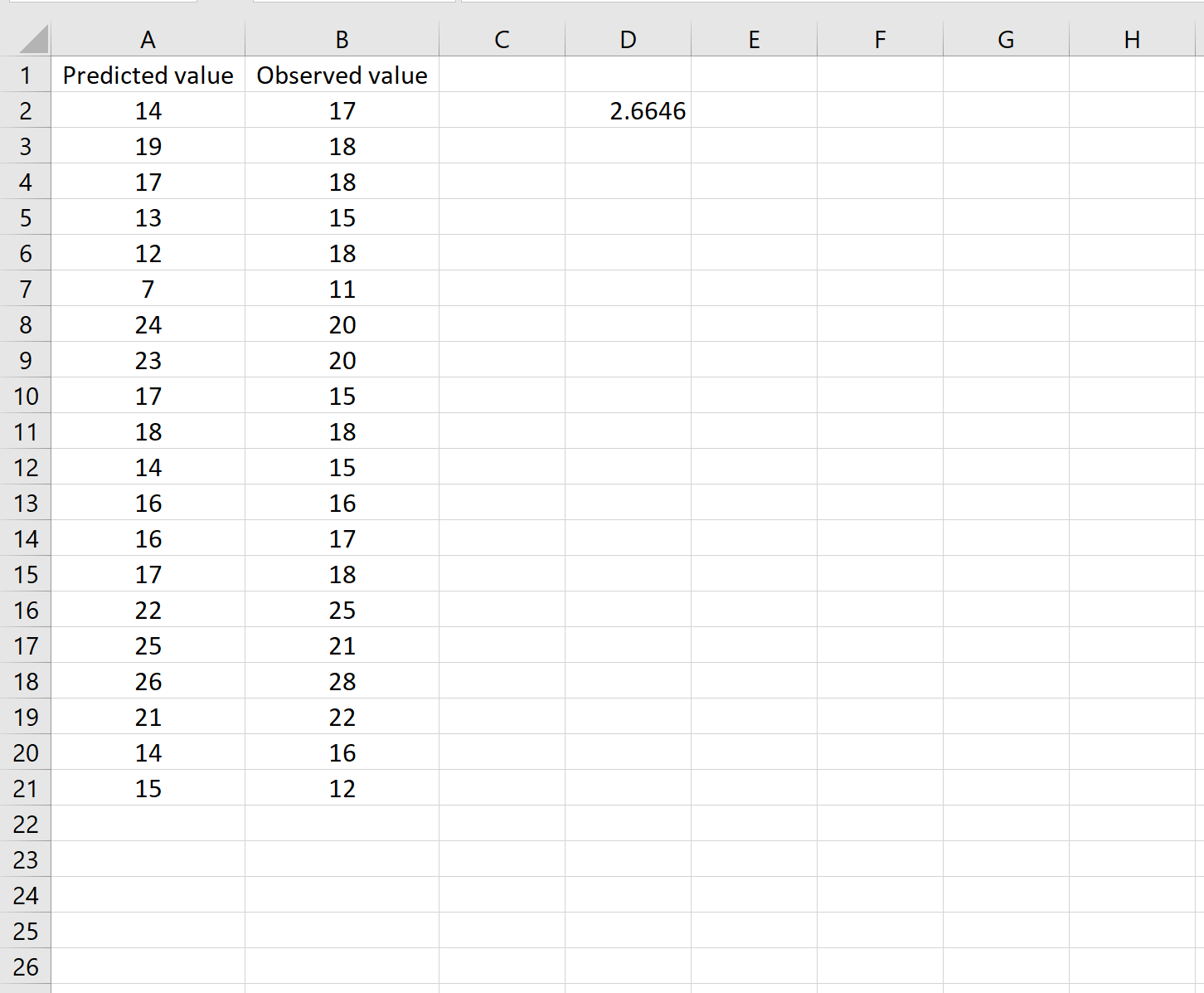
Die Formel mag etwas knifflig erscheinen, ergibt aber Sinn, wenn man sie einmal aufschlüsselt:

= SQRT( SUMSQ(A2:A21-B2:B21) / COUNT(A2:A21) )

• Zuerst berechnen wir mit der Funktion SUMSQ() die Summe der Quadrate der Differenzen zwischen den vorhergesagten und den beobachteten Werten.
• Als nächstes dividieren wir durch die Stichprobengröße des Datensatzes mit COUNTA() , das die Anzahl der Zellen in einem Bereich zählt, die nicht leer sind.
• Schließlich ziehen wir mit der Funktion SQRT() die Quadratwurzel der gesamten Berechnung.

Szenario 2

In einem anderen Szenario haben Sie möglicherweise bereits die Unterschiede zwischen vorhergesagten und beobachteten Werten berechnet. In diesem Fall haben Sie nur eine Spalte, in der die Unterschiede angezeigt werden.

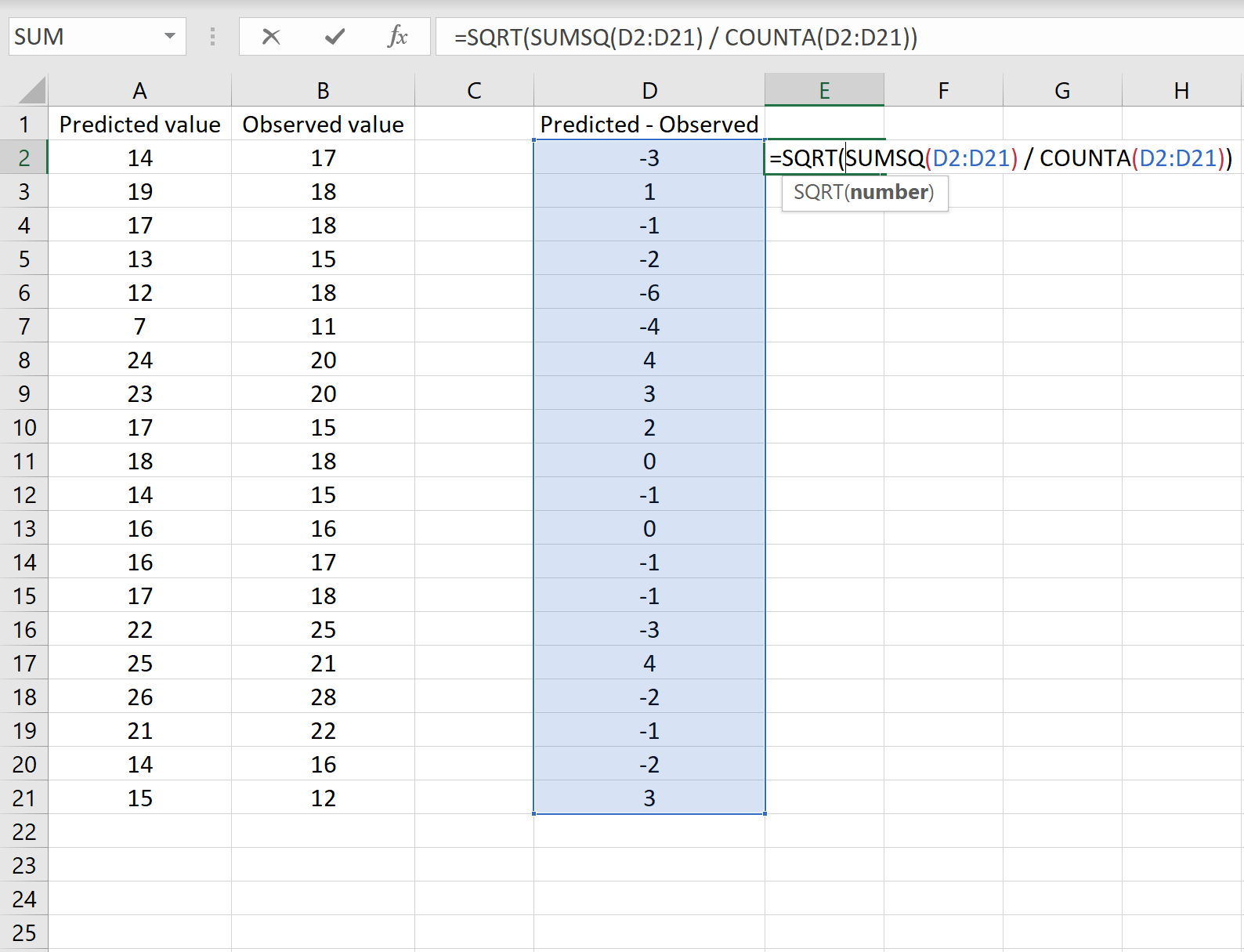
Das Bild unten zeigt ein Beispiel für dieses Szenario. Die vorhergesagten Werte werden in Spalte A angezeigt, die beobachteten Werte in Spalte B und die Differenz zwischen den vorhergesagten und beobachteten Werten in Spalte D:

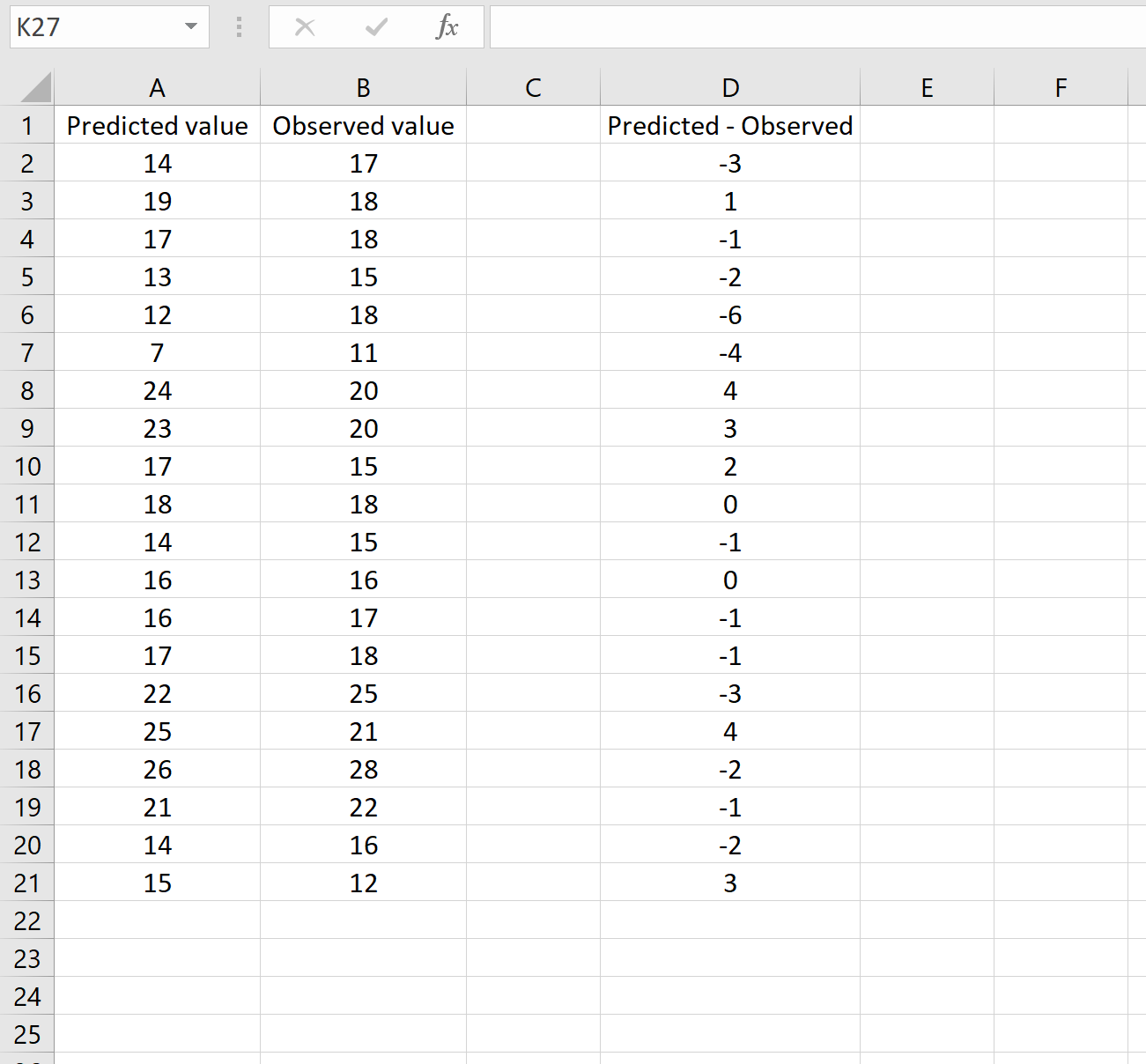
Wenn ja, können Sie den RMSE berechnen, indem Sie die folgende Formel in eine beliebige Zelle eingeben und dann auf STRG+UMSCHALT+EINGABETASTE klicken:

=SQRT(SUMSQ(D2:D21) / COUNT(D2:D21))

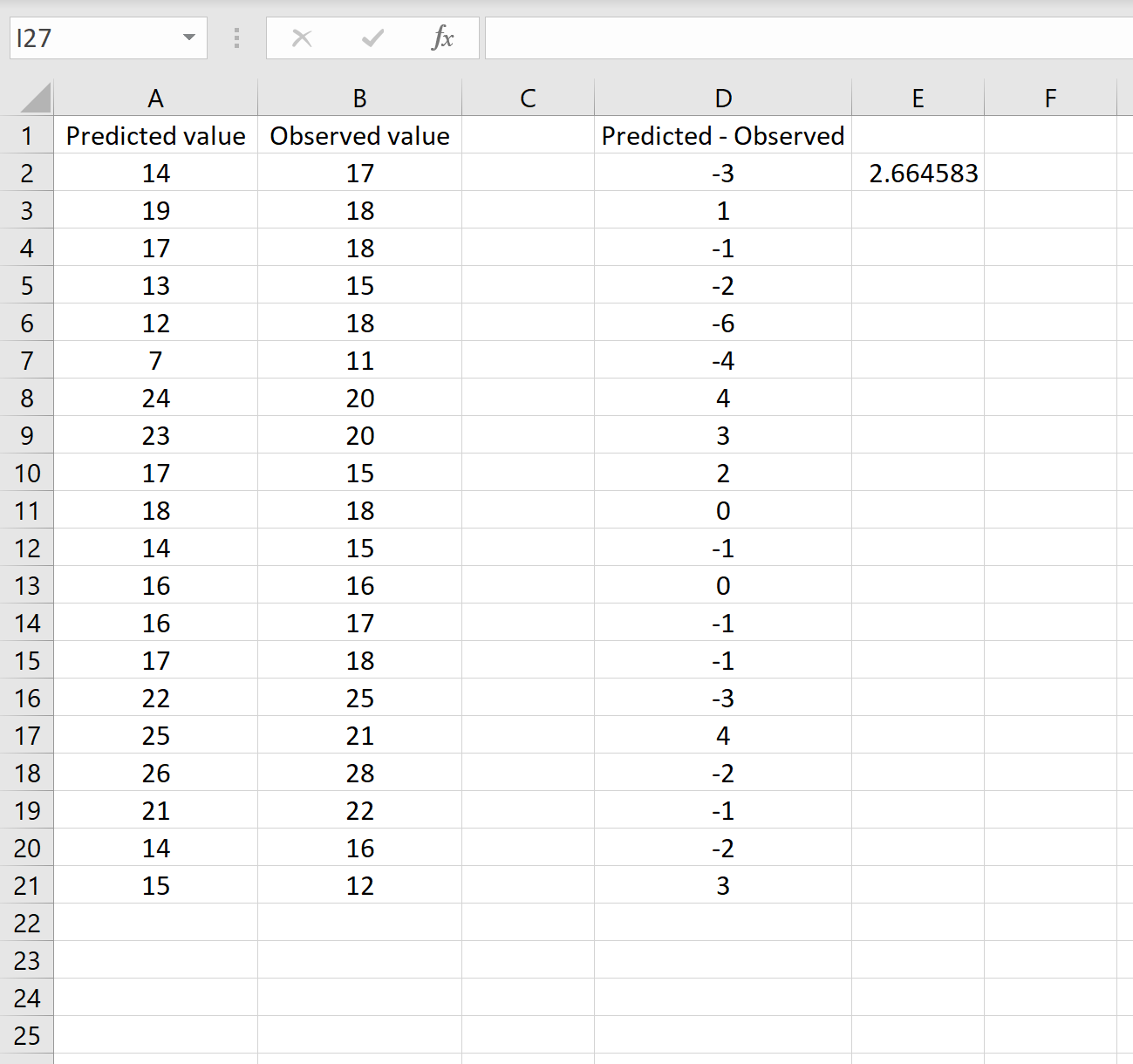
Dies sagt uns, dass der mittlere quadratische Fehler 2,6646 beträgt, was dem im ersten Szenario erzielten Ergebnis entspricht. Dies bestätigt, dass diese beiden Ansätze zur Berechnung des RMSE gleichwertig sind.

Die Formel, die wir in diesem Szenario verwendet haben, unterscheidet sich nur geringfügig von der Formel, die wir im vorherigen Szenario verwendet haben:

= SQRT( SUMSQ(D2:D21) / COUNT(D2:D21) )

• Da wir in Spalte D bereits die Differenzen zwischen den vorhergesagten und den beobachteten Werten berechnet haben, können wir die Summe der quadrierten Differenzen mit der Funktion SUMSQ() berechnen.   Funktion nur mit den Werten aus Spalte D.
• Als nächstes dividieren wir durch die Stichprobengröße des Datensatzes mit COUNTA() , das die Anzahl der Zellen in einem Bereich zählt, die nicht leer sind.
• Schließlich ziehen wir mit der Funktion SQRT() die Quadratwurzel der gesamten Berechnung .

So interpretieren Sie den RMSE

Wie bereits erwähnt, ist RMSE eine nützliche Methode, um zu sehen, wie gut ein Regressionsmodell (oder jedes Modell, das vorhergesagte Werte erzeugt) in der Lage ist, einen Datensatz „anzupassen“.

Je größer der RMSE, desto größer ist der Unterschied zwischen den vorhergesagten und den beobachteten Werten, d. h. desto schlechter passt das Regressionsmodell an die Daten. Umgekehrt gilt: Je kleiner der RMSE, desto besser kann das Modell die Daten anpassen.

Es kann besonders nützlich sein, den RMSE zweier verschiedener Modelle zu vergleichen, um herauszufinden, welches Modell am besten zu den Daten passt.

Weitere Tutorials in Excel finden Sie auf unserer Seite mit Excel-Anleitungen , auf der alle Excel-Tutorials zu Statistiken aufgeführt sind.