So führen sie eine quantilregression in python durch

Die lineare Regression ist eine Methode, mit der wir die Beziehung zwischen einer oder mehreren Prädiktorvariablen und einer Antwortvariablen verstehen können.

Wenn wir eine lineare Regression durchführen, möchten wir normalerweise den Durchschnittswert der Antwortvariablen schätzen.

Wir könnten jedoch stattdessen eine Methode namens Quantilregression verwenden, um einen beliebigen Quantil- oder Perzentilwert des Antwortwerts zu schätzen, beispielsweise das 70. Perzentil, das 90. Perzentil, das 98. Perzentil usw.

Dieses Tutorial bietet ein schrittweises Beispiel für die Verwendung dieser Funktion zur Durchführung einer Quantilregression in Python.

Schritt 1: Laden Sie die erforderlichen Pakete

Zuerst laden wir die notwendigen Pakete und Funktionen:

 import numpy as np
import pandas as pd
import statsmodels. api as sm
import statsmodels. formula . api as smf
import matplotlib. pyplot as plt

Schritt 2: Erstellen Sie die Daten

Für dieses Beispiel erstellen wir einen Datensatz mit den Lernstunden und Prüfungsergebnissen von 100 Studenten einer Universität:

 #make this example reproducible
n.p. random . seeds (0)

#create dataset
obs = 100

hours = np. random . uniform (1, 10, obs)
score = 60 + 2*hours + np. random . normal (loc=0, scale=.45*hours, size=100)

df = pd. DataFrame ({' hours ':hours, ' score ':score})

#view first five rows
df. head ()

hours score
0 5.939322 68.764553
1 7.436704 77.888040
2 6.424870 74.196060
3 5.903949 67.726441
4 4.812893 72.849046

Schritt 3: Quantilregression durchführen

Als Nächstes passen wir ein Quantil-Regressionsmodell an, wobei wir die untersuchten Stunden als Prädiktorvariable und die Prüfungsergebnisse als Antwortvariable verwenden.

Wir werden das Modell verwenden, um das erwartete 90. Perzentil der Prüfungsergebnisse basierend auf der Anzahl der gelernten Stunden vorherzusagen:

 #fit the model
model = smf. quantreg ('score~hours', df). fit (q= 0.9 )

#view model summary
print ( model.summary ())

                         QuantReg Regression Results                          
==================================================== ============================
Dept. Variable: Pseudo R-squared score: 0.6057
Model: QuantReg Bandwidth: 3.822
Method: Least Squares Sparsity: 10.85
Date: Tue, 29 Dec 2020 No. Observations: 100
Time: 15:41:44 Df Residuals: 98
                                        Model: 1
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
Intercept 59.6104 0.748 79.702 0.000 58.126 61.095
hours 2.8495 0.128 22.303 0.000 2.596 3.103
==================================================== ============================

Aus dem Ergebnis können wir die geschätzte Regressionsgleichung erkennen:

90. Perzentil der Prüfungspunktzahl = 59,6104 + 2,8495*(Stunden)

Beispielsweise sollte der 90. Perzentilwert aller Schüler, die 8 Stunden lernen, 82,4 betragen:

90. Perzentil der Prüfungspunktzahl = 59,6104 + 2,8495*(8) = 82,4 .

Die Ausgabe zeigt auch die oberen und unteren Konfidenzgrenzen für den Schnittpunkt und die Zeiten der Prädiktorvariablen an.

Schritt 4: Visualisieren Sie die Ergebnisse

Wir können die Regressionsergebnisse auch visualisieren, indem wir ein Streudiagramm mit der angepassten Quantil-Regressionsgleichung über dem Diagramm erstellen:

 #define figure and axis
fig, ax = plt.subplots(figsize=(8, 6))

#get y values
get_y = lambda a, b: a + b * hours
y = get_y( model.params [' Intercept '], model.params [' hours '])

#plot data points with quantile regression equation overlaid
ax. plot (hours, y, color=' black ')
ax. scatter (hours, score, alpha=.3)
ax. set_xlabel (' Hours Studied ', fontsize=14)
ax. set_ylabel (' Exam Score ', fontsize=14)

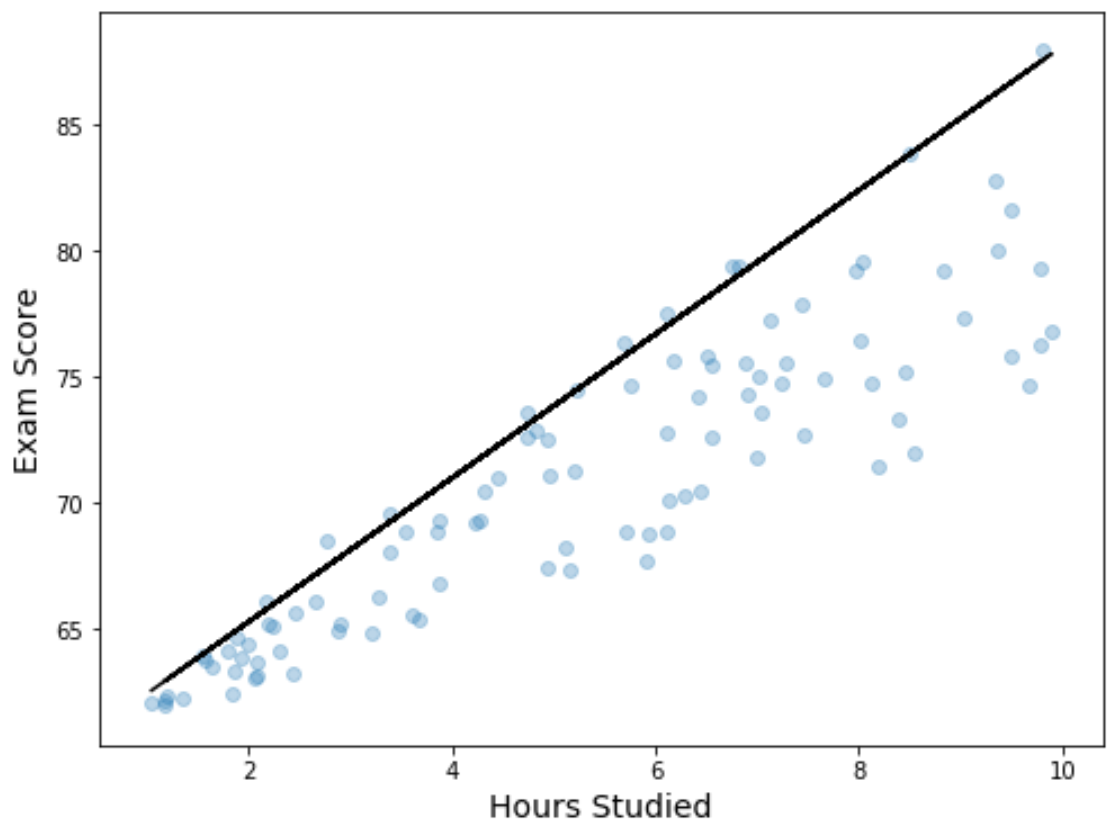
Beachten Sie, dass diese angepasste Linie im Gegensatz zu einer einfachen linearen Regressionslinie nicht die „Best-Fit-Linie“ für die Daten darstellt. Stattdessen durchläuft es das geschätzte 90. Perzentil auf jeder Ebene der Prädiktorvariablen.

Zusätzliche Ressourcen

So führen Sie eine einfache lineare Regression in Python durch
So führen Sie eine quadratische Regression in Python durch