So führen sie eine quantilregression in r durch
Die lineare Regression ist eine Methode, mit der wir die Beziehung zwischen einer oder mehreren Prädiktorvariablen und einer Antwortvariablen verstehen können.
Wenn wir eine lineare Regression durchführen, möchten wir normalerweise den Durchschnittswert der Antwortvariablen schätzen.
Wir könnten jedoch stattdessen eine Methode namens Quantilregression verwenden, um einen beliebigen Quantil- oder Perzentilwert des Antwortwerts zu schätzen, beispielsweise das 70. Perzentil, das 90. Perzentil, das 98. Perzentil usw.
Um eine Quantilregression in R durchzuführen, können wir die Funktion rq() aus dem Paket quantreg verwenden, die die folgende Syntax verwendet:
library (quantreg) model <- rq(y ~ x, data = dataset, tau = 0.5 )
Gold:
- y: die Antwortvariable
- x: die Vorhersagevariable(n)
- Daten: der Name des Datensatzes
- Tau: Das zu findende Perzentil. Der Standardwert ist der Median (Tau = 0,5), Sie können ihn jedoch auf eine beliebige Zahl zwischen 0 und 1 festlegen.
Dieses Tutorial bietet ein schrittweises Beispiel für die Verwendung dieser Funktion zur Durchführung einer Quantilregression in R.
Schritt 1: Geben Sie die Daten ein
Für dieses Beispiel erstellen wir einen Datensatz mit den Lernstunden und Prüfungsergebnissen von 100 verschiedenen Studenten einer Universität:
#make this example reproducible set.seed(0) #create data frame hours <- runif(100, 1, 10) score <- 60 + 2*hours + rnorm(100, mean=0, sd=.45*hours) df <- data.frame(hours, score) #view first six rows head(df) hours score 1 9.070275 79.22682 2 3.389578 66.20457 3 4.349115 73.47623 4 6.155680 70.10823 5 9.173870 78.12119 6 2.815137 65.94716
Schritt 2: Quantilregression durchführen
Als Nächstes passen wir ein Quantil-Regressionsmodell an, wobei wir die untersuchten Stunden als Prädiktorvariable und die Prüfungsergebnisse als Antwortvariable verwenden.
Wir werden das Modell verwenden, um das erwartete 90. Perzentil der Prüfungsergebnisse basierend auf der Anzahl der gelernten Stunden vorherzusagen:
library (quantreg) #fit model model <- rq(score ~ hours, data = df, tau = 0.9 ) #view summary of model summary(model) Call: rq(formula = score ~ hours, tau = 0.9, data = df) tau: [1] 0.9 Coefficients: coefficients lower bd upper bd (Intercept) 60.25185 59.27193 62.56459 hours 2.43746 1.98094 2.76989
Aus dem Ergebnis können wir die geschätzte Regressionsgleichung erkennen:
90. Perzentil-Prüfungsergebnis = 60,25 + 2,437*(Stunden)
Beispielsweise sollte der 90. Perzentilwert für alle Schüler, die 8 Stunden lernen, 79,75 betragen:
90. Perzentil der Prüfungspunktzahl = 60,25 + 2,437*(8) = 79,75 .
Die Ausgabe zeigt auch die oberen und unteren Konfidenzgrenzen für den Schnittpunkt und die Zeiten der Prädiktorvariablen an.
Schritt 3: Visualisieren Sie die Ergebnisse
Wir können die Regressionsergebnisse auch visualisieren, indem wir ein Streudiagramm mit der angepassten Quantil-Regressionsgleichung über dem Diagramm erstellen:
library (ggplot2) #create scatterplot with quantile regression line ggplot(df, aes(hours,score)) + geom_point() + geom_abline(intercept= coef (model)[1], slope= coef (model)[2])
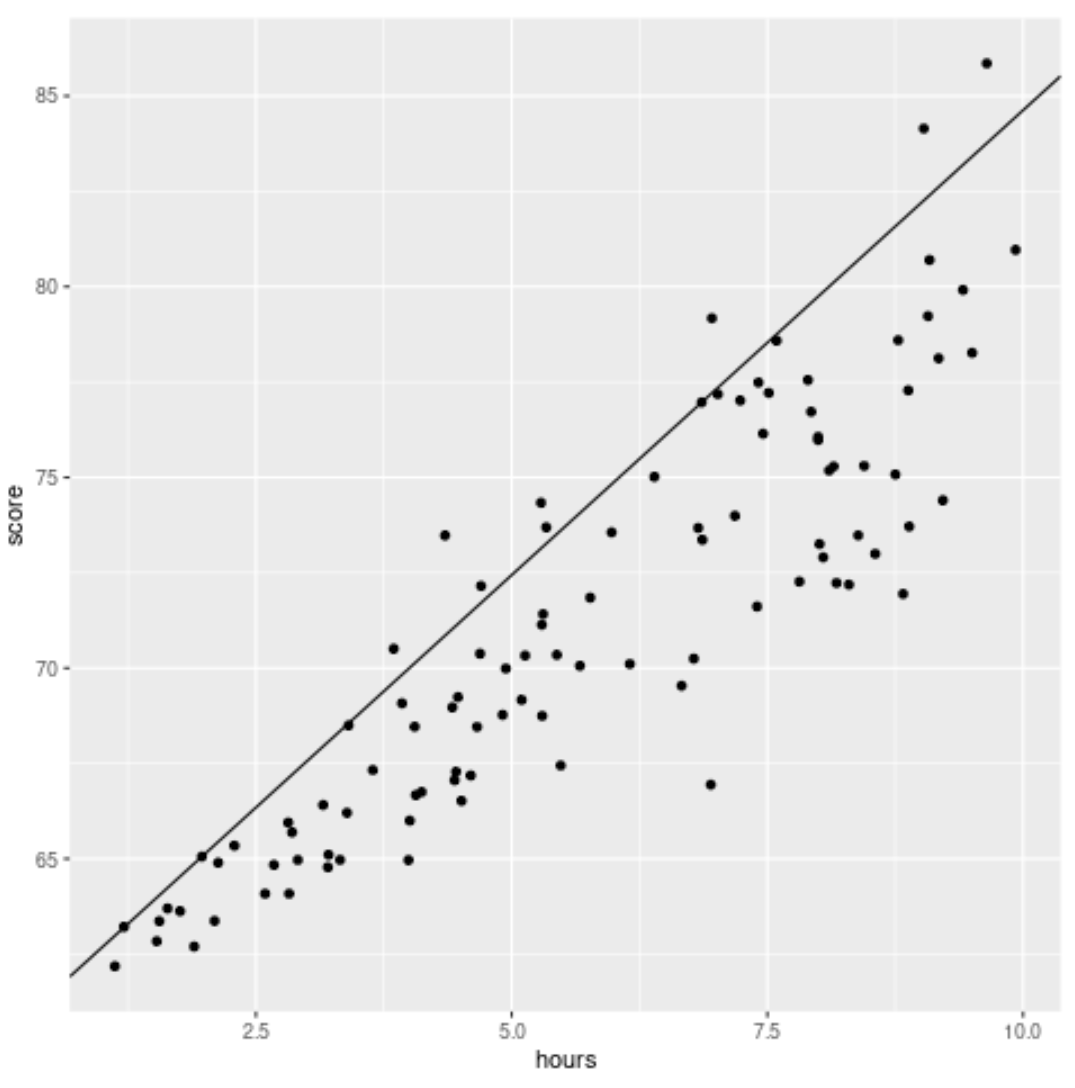
Beachten Sie, dass diese angepasste Linie im Gegensatz zu einer herkömmlichen linearen Regressionslinie nicht durch das Herzstück der Daten verläuft. Stattdessen durchläuft es das geschätzte 90. Perzentil auf jeder Ebene der Prädiktorvariablen.
Wir können den Unterschied zwischen der angepassten Quantilregressionsgleichung und der einfachen linearen Regressionsgleichung erkennen, indem wir das Argument geom_smooth() hinzufügen:
library (ggplot2) #create scatterplot with quantile regression line and simple linear regression line ggplot(df, aes(hours,score)) + geom_point() + geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) + geom_smooth(method=" lm ", se= F )
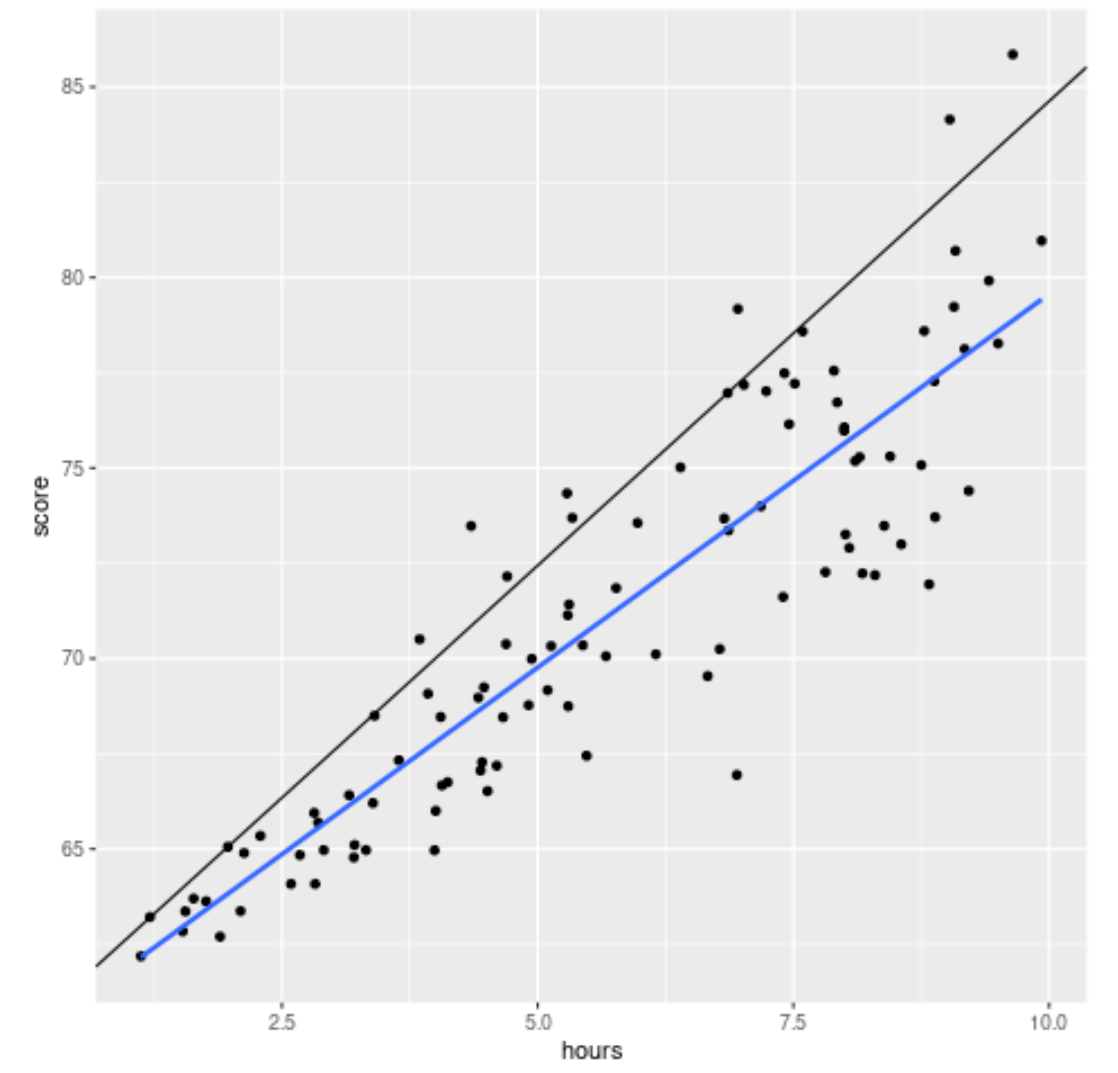
Die schwarze Linie zeigt die für das 90. Perzentil angepasste Quantil-Regressionslinie und die blaue Linie zeigt die einfache lineare Regressionslinie, die den Mittelwert der Antwortvariablen schätzt.
Wie erwartet verläuft die einfache lineare Regressionslinie durch die Daten und zeigt uns den geschätzten Mittelwert der Prüfungsergebnisse auf jeder Stundenebene.
Zusätzliche Ressourcen
Die folgenden Tutorials erklären, wie Sie andere häufige Aufgaben in R ausführen:
So führen Sie eine einfache lineare Regression in R durch
So führen Sie eine multiple lineare Regression in R durch
So führen Sie eine quadratische Regression in R durch