Quartile

In diesem Artikel erklären wir, was Quartile sind. Sie finden die Definition der einzelnen Quartile, deren Berechnung und einige konkrete Beispiele. Wir zeigen Ihnen auch, wie Sie Quartile für gruppierte Daten berechnen. Darüber hinaus können Sie Quartile jedes Datensatzes mit einem Online-Rechner berechnen.

Was sind Quartile?

In der Statistik sind Quartile die drei Werte, die einen Satz geordneter Daten in vier gleiche Teile teilen. Somit machen das erste, zweite und dritte Quartil jeweils 25 %, 50 % und 75 % aller statistischen Daten aus.

Quartile werden durch ein großes Q und den Quartilindex dargestellt, also ist das erste Quartil Q ₁ , das zweite Quartil Q ₂ und das dritte Quartil Q ₃ .

👉 Mit dem Rechner unten können Sie Quartile eines beliebigen Datensatzes berechnen.

Es ist zu beachten, dass Quartile ebenso wie Quintile, Dezile und Perzentile ein Maß für die nicht zentrale Position sind. Auf dieser Webseite können Sie überprüfen, um welche Quantiltypen es sich handelt.

erstes Quartil

Das erste Quartil , auch Quartil 1 genannt, ist der Wert, der größer als 25 % der statistischen Daten in einer Stichprobe ist. Mit anderen Worten: Das erste Quartil repräsentiert mehr als 25 % der beobachteten Daten.

Das erste Quartil wird durch das Symbol Q ₁ ausgedrückt und dient zur Bezeichnung der kleinsten Datenwerte in der Stichprobe.

zweites Quartil

Das zweite Quartil , auch Quartil 2 genannt, ist der Wert, der größer als 50 % der statistischen Daten in einer Stichprobe ist. Daher teilt das zweite Quartil den Datensatz in zwei Hälften und fällt mit dem Median und dem fünften Dezil zusammen.

Das Symbol für das zweite Quartil ist _Q2 .

drittes Quartil

Das dritte Quartil , auch 3. Quartil genannt, ist der Wert, der 75 % der statistischen Daten einer Stichprobe übersteigt. Mit anderen Worten: Das dritte Quartil repräsentiert mehr als 75 % der gesammelten Daten.

Das dritte Quartil wird durch das Symbol Q ₃ ausgedrückt und stellt die größten Werte in der Stichprobe dar.

So berechnen Sie Quartile

Um die Position der Quartile eines statistischen Datensatzes zu berechnen , müssen Sie die Anzahl der Quartile mit der Summe der Gesamtzahl der Daten plus eins multiplizieren und das Ergebnis durch vier dividieren.

Die Formel für die Quartile lautet daher wie folgt:

Bitte beachten Sie: Diese Formel gibt uns die Position des Quartils an, nicht den Wert des Quartils. Das Quartil sind die Daten, die sich an der durch die Formel ermittelten Position befinden.

Manchmal liefert uns das Ergebnis dieser Formel jedoch eine Dezimalzahl. Wir müssen also zwei Fälle unterscheiden, je nachdem, ob das Ergebnis eine Dezimalzahl ist oder nicht:

• Wenn das Ergebnis der Formel eine Zahl ohne Dezimalteil ist, ist das Quartil die Daten, die sich an der durch die obige Formel bereitgestellten Position befinden.
• Wenn das Formelergebnis eine Zahl mit einem Dezimalteil ist, wird der Quartilwert anhand der folgenden Formel berechnet:

Dabei sind x _i und x _i+1 die Zahlen der Positionen, zwischen denen sich die durch die erste Formel erhaltene Zahl befindet, und d ist der Dezimalteil der durch die erste Formel erhaltenen Zahl.

Vielleicht ist die Berechnung von Quartilen für Sie sehr kompliziert, da es viele Dinge zu berücksichtigen gilt. Aber anhand der beiden Beispiele im nächsten Abschnitt werden Sie sehen, wie einfach es eigentlich ist.

Hinweis : In der wissenschaftlichen Gemeinschaft besteht kein Konsens darüber, wie Quartile berechnet werden. Daher gibt es ein Statistikbuch, das dies etwas anders erklärt.

Beispiele für die Berechnung von Quartilen

Um vollständig zu verstehen, wie Quartile berechnet werden, finden Sie unten zwei gelöste Übungen. Im ersten sind die Quartile ganze Zahlen und im zweiten sind die Quartile Dezimalzahlen, sodass Sie sehen können, welche zwei Fälle Sie finden können.

Beispiel 1

• Berechnen Sie die drei Quartile des folgenden Datensatzes:

Wie wir oben gesehen haben, lautet die Formel zur Bestimmung von Quartilen:

In diesem Fall beträgt n die Gesamtzahl der Beobachtungen 15, daher müssen wir n durch 15 und k durch 1 ersetzen, um das erste Quartil zu finden:

Daher ist das erste Quartil die Zahl an Position vier der geordneten Werteliste, in diesem Fall 39.

Auf die gleiche Weise berechnen wir das zweite Quartil, indem wir den Koeffizienten k durch a 2 ersetzen:

Quartil 2 ist somit die achte Zahl in der sortierten Liste, die dem Wert 48 entspricht.

Abschließend wenden wir die Formel ein letztes Mal mit k =3 an, um das dritte Quartil zu berechnen:

Quartil 3 entspricht den Daten an zwölfter Stelle, also 60.

Beispiel 2

• Finden Sie die drei Quartile der folgenden Datenreihe:

In diesem zweiten Beispiel haben wir 24 Beobachtungen, daher sind die aus der Quartilformel erhaltenen Zahlen dezimal.

Wir berechnen zunächst die Position des ersten Quartils, indem wir in der allgemeinen Formel k für 1 einsetzen:

Aber wir haben die Dezimalzahl 6,25 erhalten, also liegt das erste Quartil zwischen den sechsten und siebten Daten, die 22 bzw. 25 sind. Um das genaue Quartil zu berechnen, müssen wir daher die folgende Formel anwenden:

In diesem Fall ist x _i 22, x _i+1 25 und d ist der Dezimalteil der erhaltenen Zahl, also 0,25. Noch:

Jetzt führen wir das gleiche Verfahren durch, um das zweite Quartil zu finden:

Auch hier erhalten wir eine Dezimalzahl aus der Formel, in diesem Fall ist es 12,5. Wir müssen daher dieselbe Formel für die zwölfte und dreizehnte Zahl in der Datentabelle verwenden, die 49 und 50 entspricht:

Abschließend wiederholen wir den gleichen Vorgang, um das dritte Quartil zu erhalten:

Aber die Zahl 18,75 liegt zwischen der Zahl 18 und 19, sodass das dritte Quartil zwischen den Werten dieser Positionen (71 und 73) liegen wird. Genauer gesagt ist dies der Wert, den wir aus dem folgenden Ausdruck erhalten:

Quartilrechner

Geben Sie einen statistischen Datensatz in den Rechner unten ein, um Quartile zu berechnen. Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.

Quartile in gruppierten Daten

Um Quartile zu berechnen, wenn Daten in Intervalle gruppiert werden, müssen wir zunächst mithilfe der folgenden Formel das Intervall oder die Klasse ermitteln, in die das Quartil fällt:

Das Quartil liegt daher in dem Intervall, dessen absolute kumulative Häufigkeit unmittelbar größer ist als die mit dem vorherigen Ausdruck erhaltene Zahl.

Und sobald wir das Intervall kennen, zu dem das Quartil gehört, müssen wir die folgende Formel anwenden, um den genauen Wert des Quartils zu ermitteln:

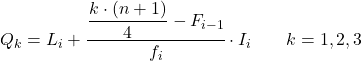
Gold:

• L _i ist die untere Grenze des Intervalls, in dem das Quartil liegt.
• n ist die Gesamtzahl der Beobachtungen.
• F _i-1 ist die kumulative absolute Häufigkeit des vorherigen Intervalls.
• f _i ist die absolute Häufigkeit des Intervalls, in dem das Quartil liegt.
• I _i ist die Breite des Quartilintervalls.

Als Beispiel sehen Sie hier eine Übung zur Berechnung von Quartilen in einer Reihe gruppierter Daten:

Um das erste Quartil zu berechnen, müssen Sie zunächst das Intervall bestimmen, in das es fällt. Dazu wenden wir die folgende Formel an:

Das erste Quartil liegt also in dem Intervall, dessen kumulative absolute Häufigkeit unmittelbar größer als 7,75 ist. In diesem Fall ist es das Intervall [50,60), dessen kumulative absolute Häufigkeit 15 beträgt. Und sobald wir das Quartilintervall kennen, verwenden wir die zweite Prozessformel :

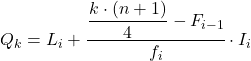
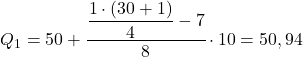
Wir wenden das gleiche Verfahren noch einmal an, um das zweite Quartil zu erhalten. Wir bestimmen zunächst das Intervall, in dem das Quartil liegt:

Das Intervall, dessen kumulative absolute Häufigkeit unmittelbar größer als 15,5 ist, ist [60,70] mit einer kumulativen absoluten Häufigkeit von 26. Das zweite Quartil ist daher:

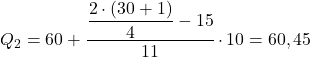
Und schließlich wiederholen wir den Vorgang, um das dritte Quartil zu finden. Wir berechnen zunächst das Intervall, das das Quartil enthält:

Die kumulative absolute Häufigkeit unmittelbar über 23,25 beträgt 26, sodass der dritte Quartilbereich [60,70] beträgt. Wir wenden daher die Formel zur Berechnung des Quartils mit diesem Intervall an:

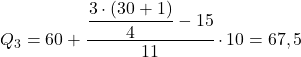
Wofür werden Quartile verwendet?

Quartile sind ein Maß für die Position und werden daher verwendet, um zu wissen, wie Daten positioniert sind. Mit anderen Worten: Anhand der Werte der drei Quartile können wir erkennen, ob ein zufälliges Datenelement in der Stichprobe sehr groß, sehr klein oder ein Durchschnittswert ist.

Wenn wir zufällig ein Datenelement aus der Stichprobe entnehmen, können wir durch einen Vergleich mit den Quartilen feststellen, ob sein Wert hoch oder niedrig ist. Wenn der Zufallsdatenwert kleiner als das erste Quartil ist, handelt es sich um einen kleinen Wert, wenn sein Wert jedoch größer als das dritte Quartil ist, handelt es sich um einen großen Wert. Liegt der Wert dieser Daten ebenfalls zwischen dem ersten und dritten Quartil, handelt es sich um einen Zwischenwert.

Andererseits werden Quartile auch zur Berechnung anderer statistischer Maße verwendet, beispielsweise des Interquartilbereichs (oder Interquartilbereichs) und zur Erstellung von Diagrammen, beispielsweise dem Box- und Whisker-Plot (oder Boxplot).