Wie man quotenverhältnisse interpretiert

In der Statistik bezieht sich die Wahrscheinlichkeit auf die Wahrscheinlichkeit, dass ein Ereignis eintritt. Es wird wie folgt berechnet:

WAHRSCHEINLICHKEIT:

P(Ereignis) = (# wünschenswerte Ergebnisse) / (# mögliche Ergebnisse)

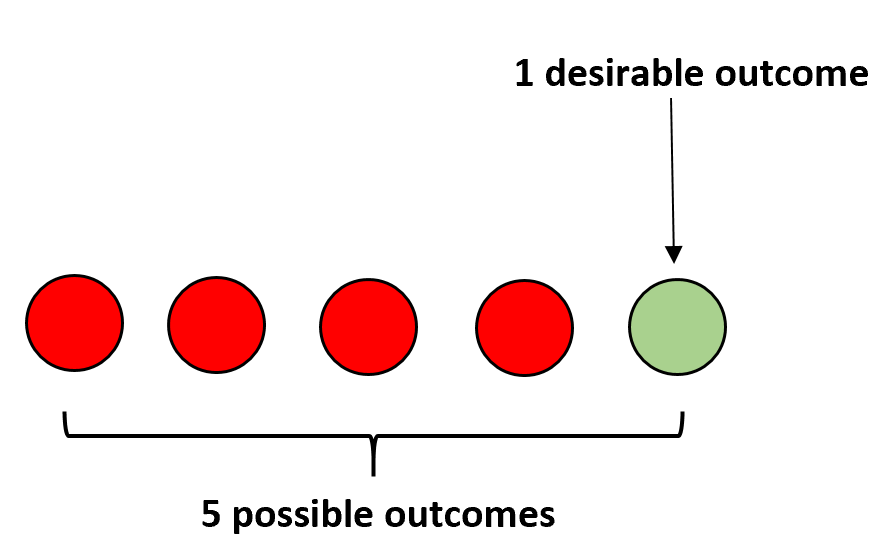
Angenommen, wir haben vier rote Bälle und einen grünen Ball in einer Tüte. Wenn Sie Ihre Augen schließen und zufällig einen Ball auswählen, berechnet sich die Wahrscheinlichkeit, dass Sie einen grünen Ball auswählen, wie folgt:

P(grün) = 1 / 5 = 0,2 .

Die Eintrittswahrscheinlichkeit eines Ereignisses lässt sich wie folgt berechnen:

CHANCEN:

Chancen (Ereignis) = P (Ereignis tritt ein) / 1-P (Ereignis tritt ein)

Beispielsweise beträgt die Wahrscheinlichkeit, einen grünen Ball zu schießen, (0,2)/1-(0,2) = 0,2/0,8 = 0,25 .

Das Odds Ratio ist das Verhältnis zweier Wahrscheinlichkeiten.

GLÜCKSBERICHT:

Quotenverhältnis = Quote von Ereignis A / Quote von Ereignis B

Wir könnten zum Beispiel das Quotenverhältnis zwischen der Wahl eines roten und eines grünen Balls berechnen.

Die Wahrscheinlichkeit, eine rote Kugel zu ziehen, beträgt 4/5 = 0,8 .

Die Wahrscheinlichkeit, eine rote Kugel zu ziehen, beträgt (0,8) / 1-(0,8) = 0,8 / 0,2 = 4 .

Das Quotenverhältnis für die Wahl eines roten Balls gegenüber einem grünen Ball wird wie folgt berechnet:

Quote (rot) / Quote (grün) = 4 / 0,25 = 16 .

Die Chance, einen roten Ball zu schießen, ist also 16-mal größer als die Chance, einen grünen Ball zu schießen.

Wann werden Quotenverhältnisse in der realen Welt verwendet?

In der realen Welt werden Quotenverhältnisse in verschiedenen Zusammenhängen verwendet, in denen Forscher die Wahrscheinlichkeit des Eintretens zweier Ereignisse vergleichen möchten. Hier sind einige Beispiele.

Beispiel Nr. 1: Quotenverhältnisse interpretieren

Forscher möchten wissen, ob eine neue Behandlung die Chancen eines Patienten auf ein positives Gesundheitsergebnis im Vergleich zu einer bestehenden Behandlung verbessert. Die folgende Tabelle zeigt die Anzahl der Patienten, bei denen es je nach Behandlung zu einem positiven oder negativen Gesundheitsergebnis kam.

Die Chancen, dass ein Patient mit der neuen Behandlung ein positives Ergebnis erzielt, lassen sich wie folgt berechnen:

Chancen = P(positiv) / 1 – P(positiv) = (50/90) / 1-(50/90) = (50/90) / (40/90) = 1,25

Die Chancen, dass ein Patient mit der bestehenden Behandlung ein positives Ergebnis erzielt, lassen sich wie folgt berechnen:

Chancen = P(positiv) / 1 – P(positiv) = (42/90) / 1-(42/90) = (42/90) / (48/90) = 0,875

Somit lässt sich die Wahrscheinlichkeit, mit der neuen Behandlung im Vergleich zur bestehenden Behandlung ein positives Ergebnis zu erzielen, wie folgt berechnen:

Quotenverhältnis = 1,25 / 0,875 = 1,428 .

Wir interpretieren dies so, dass die Wahrscheinlichkeit, dass ein Patient mit der neuen Behandlung ein positives Ergebnis erzielt, 1,428- mal höher ist als die Wahrscheinlichkeit eines Patienten, mit der bestehenden Behandlung ein positives Ergebnis zu erzielen.

Mit anderen Worten: Die Chancen auf ein positives Ergebnis erhöhen sich mit der neuen Behandlung um 42,8 % .

Beispiel #2: Quotenverhältnisse interpretieren

Vermarkter möchten wissen, ob eine Anzeige dazu führt, dass Kunden einen bestimmten Artikel häufiger kaufen als eine andere Anzeige. Sie zeigen also jede Anzeige 100 Personen. Die folgende Tabelle zeigt die Anzahl der Personen, die den Artikel gekauft haben, basierend auf der Anzeige, die sie gesehen haben:

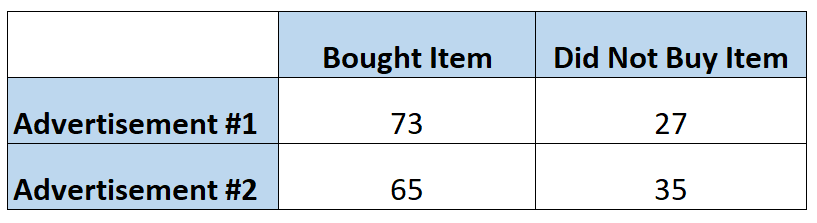
Die Wahrscheinlichkeit, dass eine Einzelperson den Artikel kauft, nachdem sie die erste Anzeige gesehen hat, lässt sich wie folgt berechnen:

Quote = P(gekauft) / 1 – P(gekauft) = (73/100) / 1-(73/100) = (73/100) / (27/100) = 2,704

Die Wahrscheinlichkeit, dass eine Einzelperson den Artikel kauft, nachdem sie die zweite Anzeige gesehen hat, lässt sich wie folgt berechnen:

Quote = P(gekauft) / 1 – P(gekauft) = (65/100) / 1-(65/10) = (65/100) / (35/100) = 1,857

Das Verhältnis der Wahrscheinlichkeit, dass ein Kunde den Artikel kauft, nachdem er die erste Anzeige gesehen hat, im Vergleich zu einem Kauf, nachdem er die zweite Anzeige gesehen hat, kann also wie folgt berechnet werden:

Quotenverhältnis = 2,704 / 1,857 = 1,456 .

Wir interpretieren dies so, dass die Wahrscheinlichkeit, dass eine Einzelperson den Artikel kauft, nachdem sie die erste Anzeige gesehen hat , 1,456- mal höher ist als die Wahrscheinlichkeit , dass eine Einzelperson den Artikel kauft, nachdem sie die zweite Anzeige gesehen hat.

Mit anderen Worten: Die Kaufchancen des Artikels erhöhen sich durch die Erstlistung um 45,6 % .

Zusätzliche Ressourcen

So berechnen Sie das Odds Ratio und das relative Risiko in Excel
So interpretieren Sie ein Odds Ratio von weniger als 1
Wie ist das relative Risiko zu interpretieren?