Kurvenanpassung in r (mit beispielen)

Oft möchten Sie möglicherweise die Gleichung finden, die am besten zu einer Kurve von R passt.

Das folgende Schritt-für-Schritt-Beispiel erklärt, wie man mit der Funktion poly() Kurven an Daten in R anpasst und wie man ermittelt, welche Kurve am besten zu den Daten passt.

Schritt 1: Daten erstellen und visualisieren

Beginnen wir mit der Erstellung eines gefälschten Datensatzes und erstellen dann ein Streudiagramm, um die Daten zu visualisieren:

 #create data frame
df <- data. frame (x=1:15,
                 y=c(3, 14, 23, 25, 23, 15, 9, 5, 9, 13, 17, 24, 32, 36, 46))

#create a scatterplot of x vs. y
plot(df$x, df$y, pch= 19 , xlab=' x ', ylab=' y ') 

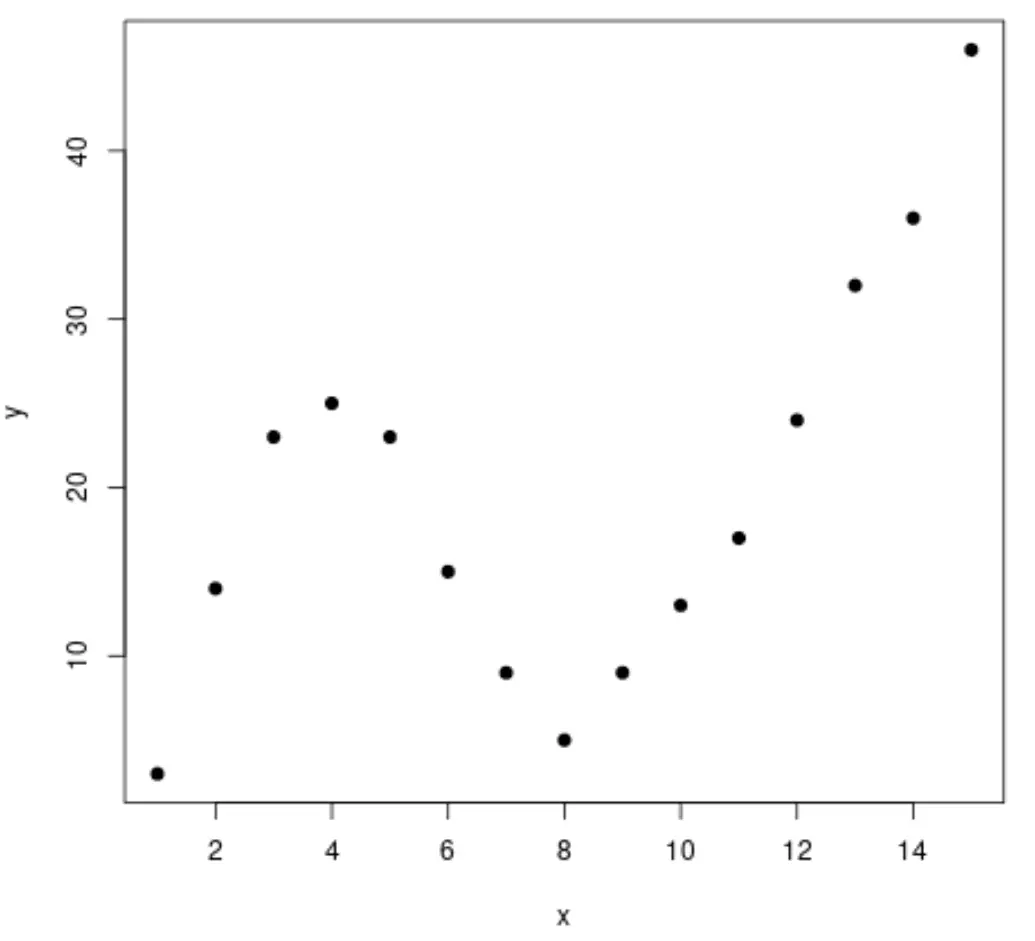
Schritt 2: Passen Sie mehrere Kurven an

Passen wir dann mehrere polynomiale Regressionsmodelle an die Daten an und visualisieren die Kurve jedes Modells im selben Diagramm:

 #fit polynomial regression models up to degree 5
fit1 <- lm(y~x, data=df)
fit2 <- lm(y~poly(x,2,raw= TRUE ), data=df)
fit3 <- lm(y~poly(x,3,raw= TRUE ), data=df)
fit4 <- lm(y~poly(x,4,raw= TRUE ), data=df)
fit5 <- lm(y~poly(x,5,raw= TRUE ), data=df)

#create a scatterplot of x vs. y
plot(df$x, df$y, pch=19, xlab=' x ', ylab=' y ')

#define x-axis values
x_axis <- seq(1, 15, length= 15 )

#add curve of each model to plot
lines(x_axis, predict(fit1, data. frame (x=x_axis)), col=' green ')
lines(x_axis, predict(fit2, data. frame (x=x_axis)), col=' red ')
lines(x_axis, predict(fit3, data. frame (x=x_axis)), col=' purple ')
lines(x_axis, predict(fit4, data. frame (x=x_axis)), col=' blue ')
lines(x_axis, predict(fit5, data. frame (x=x_axis)), col=' orange ')

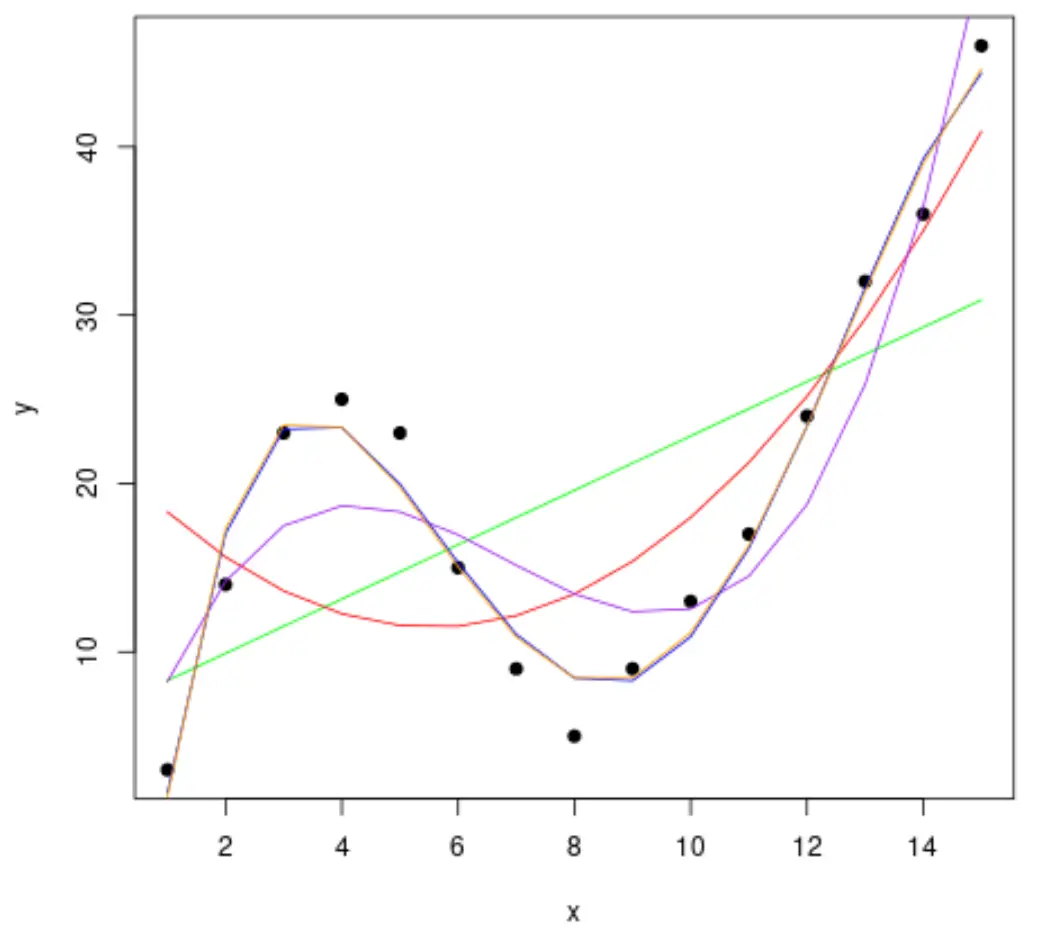
Um zu bestimmen, welche Kurve am besten zu den Daten passt, können wir uns das angepasste R-Quadrat jedes Modells ansehen.

Dieser Wert gibt uns den Prozentsatz der Variation in der Antwortvariablen an, der durch die Prädiktorvariablen im Modell erklärt werden kann, angepasst an die Anzahl der Prädiktorvariablen.

 #calculated adjusted R-squared of each model
summary(fit1)$adj. r . squared
summary(fit2)$adj. r . squared
summary(fit3)$adj. r . squared
summary(fit4)$adj. r . squared
summary(fit5)$adj. r . squared

[1] 0.3144819
[1] 0.5186706
[1] 0.7842864
[1] 0.9590276
[1] 0.9549709

Aus dem Ergebnis können wir ersehen, dass das Modell mit dem höchsten angepassten R-Quadrat das Polynom vierten Grades ist, das einen angepassten R-Quadrat von 0,959 aufweist.

Schritt 3: Visualisieren Sie die endgültige Kurve

Schließlich können wir ein Streudiagramm mit der Kurve des Polynommodells vierten Grades erstellen:

 #create a scatterplot of x vs. y
plot(df$x, df$y, pch=19, xlab=' x ', ylab=' y ')

#define x-axis values
x_axis <- seq(1, 15, length= 15 )

#add curve of fourth-degree polynomial model
lines(x_axis, predict(fit4, data. frame (x=x_axis)), col=' blue ')

Wir können die Gleichung für diese Zeile auch mit der Funktion summary() erhalten:

 summary(fit4)

Call:
lm(formula = y ~ poly(x, 4, raw = TRUE), data = df)

Residuals:
    Min 1Q Median 3Q Max 
-3.4490 -1.1732 0.6023 1.4899 3.0351 

Coefficients:
                         Estimate Std. Error t value Pr(>|t|)    
(Intercept) -26.51615 4.94555 -5.362 0.000318 ***
poly(x, 4, raw = TRUE)1 35.82311 3.98204 8.996 4.15e-06 ***
poly(x, 4, raw = TRUE)2 -8.36486 0.96791 -8.642 5.95e-06 ***
poly(x, 4, raw = TRUE)3 0.70812 0.08954 7.908 1.30e-05 ***
poly(x, 4, raw = TRUE)4 -0.01924 0.00278 -6.922 4.08e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.424 on 10 degrees of freedom
Multiple R-squared: 0.9707, Adjusted R-squared: 0.959 
F-statistic: 82.92 on 4 and 10 DF, p-value: 1.257e-07

Die Gleichung der Kurve lautet wie folgt:

y = -0,0192x ⁴ + 0,7081x ³ – 8,3649x ² + 35,823x – 26,516

Wir können diese Gleichung verwenden, um den Wert der Antwortvariablen basierend auf den Prädiktorvariablen im Modell vorherzusagen. Wenn zum Beispiel x = 4, dann würden wir y = 23,34 vorhersagen:

y = -0,0192(4) ⁴ + 0,7081(4) ³ – 8,3649(4) ² + 35,823(4) – 26,516 = 23,34

Zusätzliche Ressourcen

Eine Einführung in die Polynomregression
Polynomielle Regression in R (Schritt für Schritt)
So verwenden Sie die seq-Funktion in R