R vs. r-quadrat: was ist der unterschied?
Zwei Begriffe, die Studierende in der Statistik oft verwechseln, sind R und R-Quadrat , oft geschrieben als R2 .
Im Kontext einer einfachen linearen Regression :
- A: Die Korrelation zwischen der Prädiktorvariablen x und der Antwortvariablen y.
- R 2 : Anteil der Varianz der Antwortvariablen, der durch die Prädiktorvariable im Regressionsmodell erklärt werden kann.
Und im Kontext einer multiplen linearen Regression :
- A: Die Korrelation zwischen den beobachteten Werten der Antwortvariablen und den vom Modell vorhergesagten Werten der Antwortvariablen.
- R 2 : Anteil der Varianz der Antwortvariablen, der durch die Prädiktorvariablen des Regressionsmodells erklärt werden kann.
Beachten Sie, dass der Wert von R 2 zwischen 0 und 1 liegt. Je näher der Wert bei 1 liegt, desto stärker ist die Beziehung zwischen der/den Prädiktorvariablen und der Antwortvariablen.
Die folgenden Beispiele zeigen, wie R- und R-Quadrat-Werte in einfachen linearen Regressionsmodellen und mehreren linearen Regressionsmodellen interpretiert werden.
Beispiel 1: Einfache lineare Regression
Angenommen, wir haben den folgenden Datensatz, der die Lernstunden und Prüfungsergebnisse von 12 Studenten in einem bestimmten Mathematikkurs zeigt:
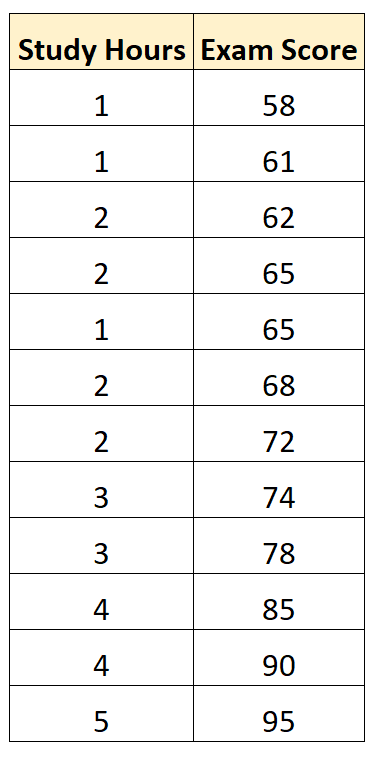
Mit statistischer Software (wie Excel, R, Python, SPSS usw.) können wir ein einfaches lineares Regressionsmodell anpassen, indem wir „Studienstunden“ als Prädiktorvariable und „Prüfungsnote“ als Antwortvariable verwenden.
Für dieses Modell finden wir folgende Ausgabe:
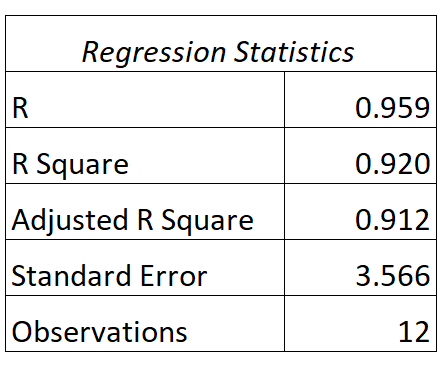
So interpretieren Sie die R- und R-Quadrat-Werte dieses Modells:
- A: Die Korrelation zwischen Lernstunden und Prüfungsergebnis beträgt 0,959 .
- R 2 : Das R-Quadrat für dieses Regressionsmodell beträgt 0,920 . Dies zeigt uns, dass 92,0 % der Unterschiede in den Prüfungsergebnissen durch die Anzahl der gelernten Stunden erklärt werden können.
Beachten Sie auch, dass der R 2 -Wert einfach dem quadrierten R-Wert entspricht:
R2 = R * R = 0,959 * 0,959 = 0,920
Beispiel 2: Multiple lineare Regression
Angenommen, wir haben den folgenden Datensatz, der die gelernten Stunden, die aktuelle Schülernote und die Prüfungsnote von 12 Schülern in einem bestimmten Mathematikkurs zeigt:
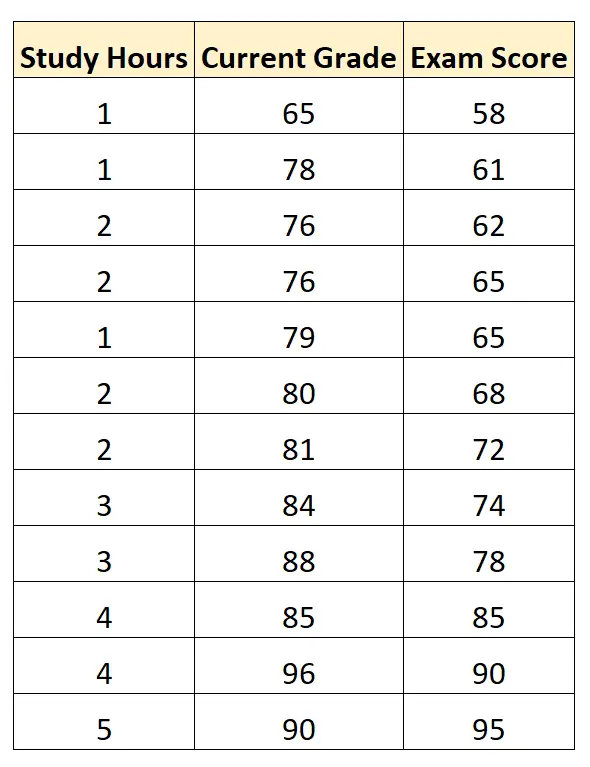
Mithilfe von Statistiksoftware können wir ein multiples lineares Regressionsmodell anpassen, indem wir „Studienstunden“ und „aktuelle Note“ als Prädiktorvariablen und „Prüfungsnote“ als Antwortvariable verwenden.
Für dieses Modell finden wir folgende Ausgabe:
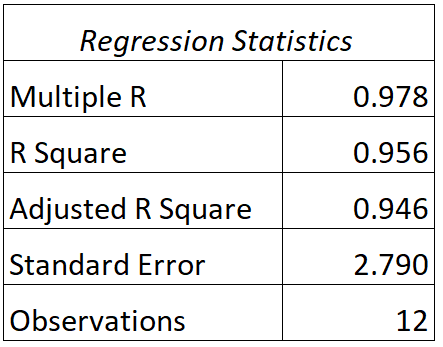
So interpretieren Sie die R- und R-Quadrat-Werte dieses Modells:
- A: Die Korrelation zwischen den tatsächlichen Testergebnissen und den vorhergesagten Testergebnissen des Modells beträgt 0,978 .
- R 2 : Das R-Quadrat für dieses Regressionsmodell beträgt 0,956 . Dies zeigt uns, dass 95,6 % der Abweichungen bei den Prüfungsergebnissen durch die Anzahl der gelernten Stunden und die aktuelle Note des Schülers in der Klasse erklärt werden können.
Beachten Sie auch, dass der R 2 -Wert einfach dem quadrierten R-Wert entspricht:
R2 = R * R = 0,978 * 0,978 = 0,956
Zusätzliche Ressourcen
Was ist ein guter R-Quadrat-Wert?
Ein sanfter Leitfaden zur Quadratsumme: SST, SSR, SSE