Eine einführung in die rayleigh-verteilung

Die Rayleigh-Verteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die zur Modellierung von Zufallsvariablen verwendet wird, die nur Werte gleich oder größer als Null annehmen können.

Es hat die folgende Wahrscheinlichkeitsdichtefunktion:

f(x; σ) = (x/σ ² )e ^{-x 2 /(2σ 2 )}

wobei σ der Skalenparameter der Verteilung ist.

Eigenschaften der Rayleigh-Verteilung

Die Rayleigh-Verteilung hat die folgenden Eigenschaften:

• Durchschnitt: σ√ π/2
• Abweichung: ((4-π)/2)σ ²
• Modus: σ

Da π einen bekannten numerischen Wert hat, können wir die Eigenschaften wie folgt vereinfachen:

• Durchschnitt: 1,253σ
• Abweichung: 0,429σ ²
• Modus: σ

Visualisierung der Rayleigh-Verteilung

Die folgende Grafik zeigt die Form der Rayleigh-Verteilung, da sie unterschiedliche Werte für den Skalenparameter annimmt:

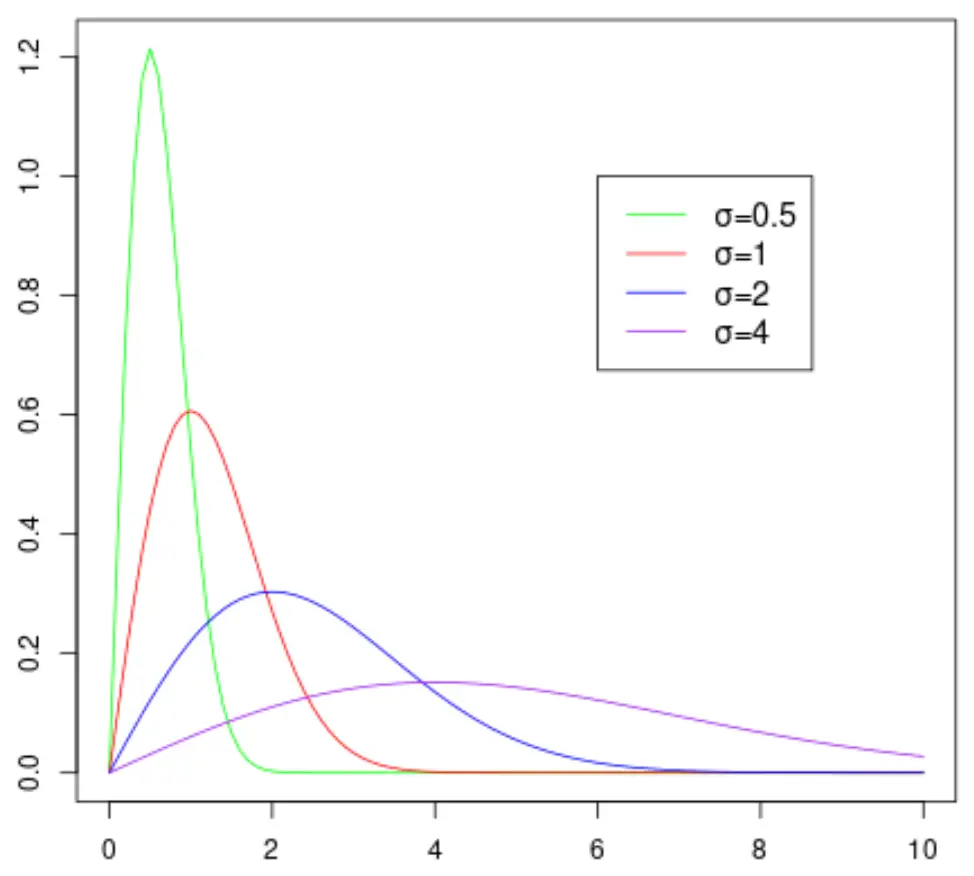
Beachten Sie, dass die Verteilung umso breiter wird, je größer der Wert des Skalenparameters σ ist.

Bonus: Für diejenigen, die neugierig sind: Wir haben den folgenden R-Code verwendet, um das obige Diagramm zu erstellen:

 #load VGAM package
library (VGAM)

#create density plots
curve(drayleigh(x, scale = 0.5), from=0, to=10, col='green')
curve(drayleigh(x, scale = 1), from=0, to=10, col='red', add=TRUE)
curve(drayleigh(x, scale = 2), from=0, to=10, col='blue', add=TRUE)
curve(drayleigh(x, scale = 4), from=0, to=10, col='purple', add=TRUE)

#add legend
legend(6, 1, legend=c("σ=0.5", "σ=1", "σ=2", "σ=4"),
       col=c("green", "red", "blue", "purple"), lty=1, cex=1.2)

Beziehung zu anderen Distributionen

Die Rayleigh-Verteilung hat die folgende Beziehung zu anderen Wahrscheinlichkeitsverteilungen:

1. Wenn der Skalenparameter (σ) gleich 1 ist, entspricht die Rayleigh-Verteilung einer Chi-Quadrat-Verteilung mit 2 Freiheitsgraden.

2. Die Rayleigh-Verteilung ist ein Sonderfall der Weibull-Verteilung mit einem Formparameter k = 2.

3. Die Rayleigh-Verteilung mit Skalenparameter σ ist gleich der Rice-Verteilung mit Rice(0, σ).

Anwendungen

In der Praxis wird die Rayleigh-Verteilung in verschiedenen Anwendungen verwendet, darunter:

1. Die Rayleigh-Verteilung wird verwendet, um das Verhalten von Wellen im Ozean zu modellieren, einschließlich der Zeit, die die Wellen benötigen, um ihren Kamm zu erreichen, und der maximalen Höhe, die die Wellen erreichen.

2. Die Rayleigh-Verteilung wird verwendet, um das Verhalten von Hintergrunddaten in der Magnetresonanztomographie, besser bekannt als MRT, zu modellieren.

3. Die Rayleigh-Verteilung wird im Bereich der Ernährung verwendet, um den Zusammenhang zwischen Nährstoffniveaus und Ernährungsreaktion bei Menschen und Tieren zu modellieren.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu anderen Verteilungen in der Statistik:

Eine Einführung in die Normalverteilung
Eine Einführung in die Binomialverteilung
Eine Einführung in die Poisson-Verteilung