Regressionslinie

Von Dr. Benjamin Anderson August 2, 2023 Statistiken Keine Kommentare

In diesem Artikel wird erklärt, was eine Regressionslinie in der Statistik ist. So finden Sie Informationen zur Berechnung der Regressionsgeraden zwischen zwei Variablen, eine gelöste Übung und darüber hinaus einen Online-Rechner zur Berechnung der Regressionsgeraden für jede Datenstichprobe.

Was ist die Regressionslinie?

In der Statistik ist die Regressionsgerade die Linie, die aus einem einfachen linearen Regressionsmodell erhalten wird. Genauer gesagt ist die Regressionslinie die Linie, die am besten zu einem Streudiagramm passt und daher einen Satz statistischer Daten am besten beschreibt.

Somit setzt die Regressionsgeradengleichung die unabhängige Variable X und die abhängige Variable Y eines Datensatzes mathematisch in Beziehung. Obwohl die Regressionsgerade im Allgemeinen nicht in der Lage ist, den Wert jeder Beobachtung genau zu bestimmen, kann sie eine Annäherung an ihren Wert liefern.

Wie Sie in der vorherigen Grafik sehen können, hilft uns die Regressionslinie dabei, den Trend eines Datensatzes zu erkennen und zu erkennen, welche Art von Beziehung zwischen der unabhängigen Variablen und der abhängigen Variablen besteht. Im Folgenden betrachten wir Anwendungen der Regressionsgeraden.

Regressionslinienformel

Nachdem wir nun die Definition der Regressionsgeraden kennen, sehen wir uns an, wie die Gleichung der Geraden eines linearen Regressionsmodells berechnet wird.

Wie jede Gerade besteht die Gleichung der Regressionsgeraden aus einer Konstante (b ₀ ) und einer Steigung (b ₁ ):

$y=b_0+b_1x$

Somit lauten die Formeln zur Berechnung der Koeffizienten der linearen Regressionsgeraden wie folgt:

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[12ex]b_0=\overline{y}-b_1\overline{x}\end{array}$

Gold:

$b_0$

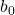
ist die Konstante der Regressionsgeraden.
$b_1$

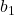
ist die Steigung der Regressionsgeraden.
$x_i$

ist der Wert der unabhängigen Variablen X der Daten i.
$y_i$

ist der Wert der abhängigen Variablen Y der Daten i.
$\overline{x}$

ist der Durchschnitt der Werte der unabhängigen Variablen
$\overline{y}$

ist der Durchschnitt der Werte der abhängigen Variablen Y.

👉 Mit dem Rechner unten können Sie die Regressionsgerade für jeden Datensatz berechnen.

Konkretes Beispiel der Regressionsgeraden

Um das Konzept einer Regressionslinie weiter zu untersuchen, finden Sie unten ein Beispiel für die Erstellung einer Regressionslinie.

Nach der Ablegung einer Statistikprüfung wurden fünf Studenten gefragt, wie viele Stunden sie für die Prüfung aufgewendet hatten. Die Daten sind in der folgenden Tabelle aufgeführt. Berechnen Sie die Regressionsgerade aus den gesammelten statistischen Daten, um die Lernstunden linear mit der erzielten Note in Beziehung zu setzen. Bestimmen Sie als Nächstes, welche Note ein Schüler erhält, der 8 Stunden gelernt hat.

Um die Regressionsgerade für die Beispieldaten zu finden, müssen wir die Koeffizienten b ₀ und b ₁ der Gleichung bestimmen und dazu die Formeln aus dem obigen Abschnitt verwenden.

Um jedoch die Formeln für die lineare Regressionsgerade anzuwenden, müssen wir zunächst den Mittelwert der unabhängigen Variablen und den Mittelwert der abhängigen Variablen berechnen:

$\begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}$

Nachdem wir nun die Mittelwerte der Variablen kennen, berechnen wir den Koeffizienten b ₁ des Modells mithilfe der entsprechenden Formel:

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}$

Schließlich berechnen wir den Koeffizienten b ₀ des Modells mithilfe der entsprechenden Formel:

$\begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}$

Kurz gesagt lautet die Gleichung der linearen Regressionslinie des Problems wie folgt:

$y=2,0294+0,4412x$

Unten sehen Sie die grafische Darstellung der Beispieldaten sowie die Gerade des einfachen linearen Regressionsmodells:

Beispiel einer linearen Regressionslinie

Sobald wir die Regressionsgerade berechnet haben, setzen Sie diesen Wert einfach in die Gleichung der erhaltenen Regressionsgerade ein, um die Note vorherzusagen, die ein Schüler erhalten wird, der 8 Stunden studiert hat:

$y=2,0294+0,4412\cdot 8=5,56$

Nach dem durchgeführten linearen Regressionsmodell erhält ein Student, der acht Stunden lang lernt, in der Prüfung eine Punktzahl von 5,56.

Wozu dient eine Regressionsgerade?

Die Regressionsgerade hat im Wesentlichen zwei Verwendungszwecke: Die Regressionsgerade wird verwendet, um festzustellen, welche Art von Beziehung zwischen zwei Variablen besteht, und andererseits ermöglicht die Regressionsgerade auch eine Vorhersage über den Wert einer neuen Beobachtung.

Die Steigung der Regressionsgeraden sagt uns, wie die Korrelation zwischen der unabhängigen Variablen und der abhängigen Variablen ist. Wenn die Steigung positiv ist, bedeutet dies, dass die abhängige Variable direkt proportional zur unabhängigen Variablen ist. Wenn die Steigung negativ ist, bedeutet dies, dass die Variablen umgekehrt proportional sind. Liegt der Steigungskoeffizient schließlich sehr nahe bei Null, bedeutet dies, dass die Korrelation zwischen den beiden Variablen sehr schwach ist.

Wenn außerdem die Gleichung der Regressionsgeraden bekannt ist, kann der Wert der abhängigen Variablen für einen neuen Wert der unabhängigen Variablen vorhergesagt werden, wie wir es im obigen Beispiel getan haben. Je besser also die Regressionsgerade angepasst ist, desto besser sind die Vorhersagen.

Regressionslinienrechner

Geben Sie eine Stichprobe von Daten in den folgenden Rechner ein, um die Regressionslinie zwischen den beiden Variablen zu berechnen. Sie müssen die Datenpaare trennen, sodass im ersten Feld nur die Werte der unabhängigen Variablen X und im zweiten Feld nur die Werte der abhängigen Variablen Y stehen.

Die Daten müssen durch ein Leerzeichen getrennt und mit dem Punkt als Dezimaltrennzeichen eingegeben werden.

Über den Autor

Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen