Was ist eine bereichsbeschränkung?

In der Statistik versuchen wir oft, die Korrelation zwischen zwei Variablen zu messen. Dies hilft uns, Folgendes zu verstehen:

• Die Richtung der Beziehung zwischen zwei Variablen. Nimmt die andere Variable tendenziell zu oder ab, wenn eine Variable zunimmt?
• Die Stärke der Beziehung zwischen zwei Variablen. Wie stark ändert sich der Wert der beiden Variablen?

Leider kann bei der Messung der Korrelation zwischen zwei Variablen ein Problem auftreten, das als Bereichseinschränkung bezeichnet wird. Dies geschieht, wenn der Messwertbereich für eine der Variablen aus irgendeinem Grund eingeschränkt ist.

Angenommen, wir möchten die Korrelation zwischen Lernstunden und Prüfungsergebnissen von Schülern einer bestimmten Schule messen.

Wenn wir Daten zu diesen beiden Variablen für alle 1.000 Schüler der Schule sammeln, könnten wir feststellen, dass die Korrelation zwischen den Lernstunden und den Prüfungsergebnissen 0,73 beträgt.

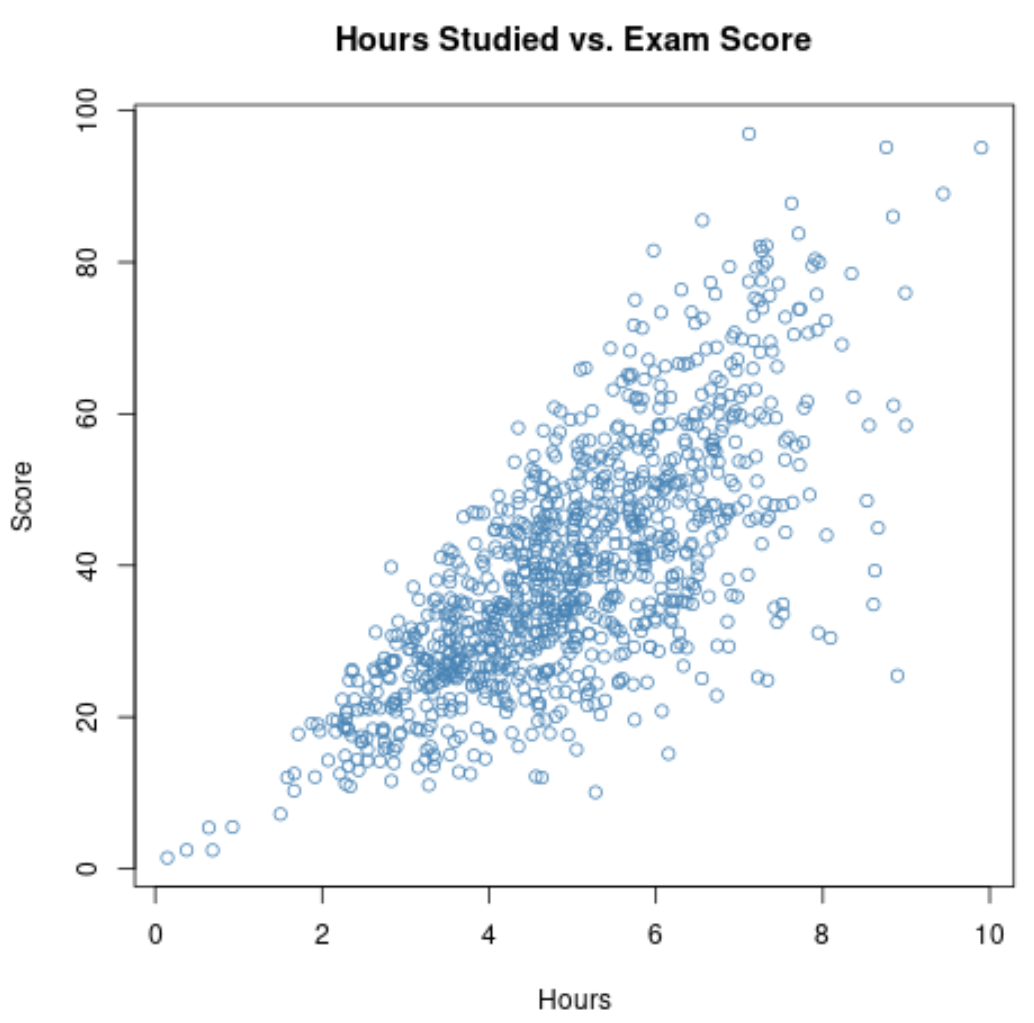
Diese Korrelation ist recht hoch, was auf eine starke positive Beziehung zwischen den beiden Variablen hinweist. Je mehr Studierende lernen, desto besser schneiden sie bei Prüfungen ab.

Gehen wir jedoch davon aus, dass wir nur Daten zu Studierenden in Honours-Studiengängen sammeln. Es könnte sein, dass alle diese Schüler mindestens 6 Stunden gelernt haben.

Wenn wir also die Korrelation zwischen den Lernstunden und den Prüfungsergebnissen dieser Schüler berechnen, würden wir einen engen Bereich für variable Lernstunden verwenden.

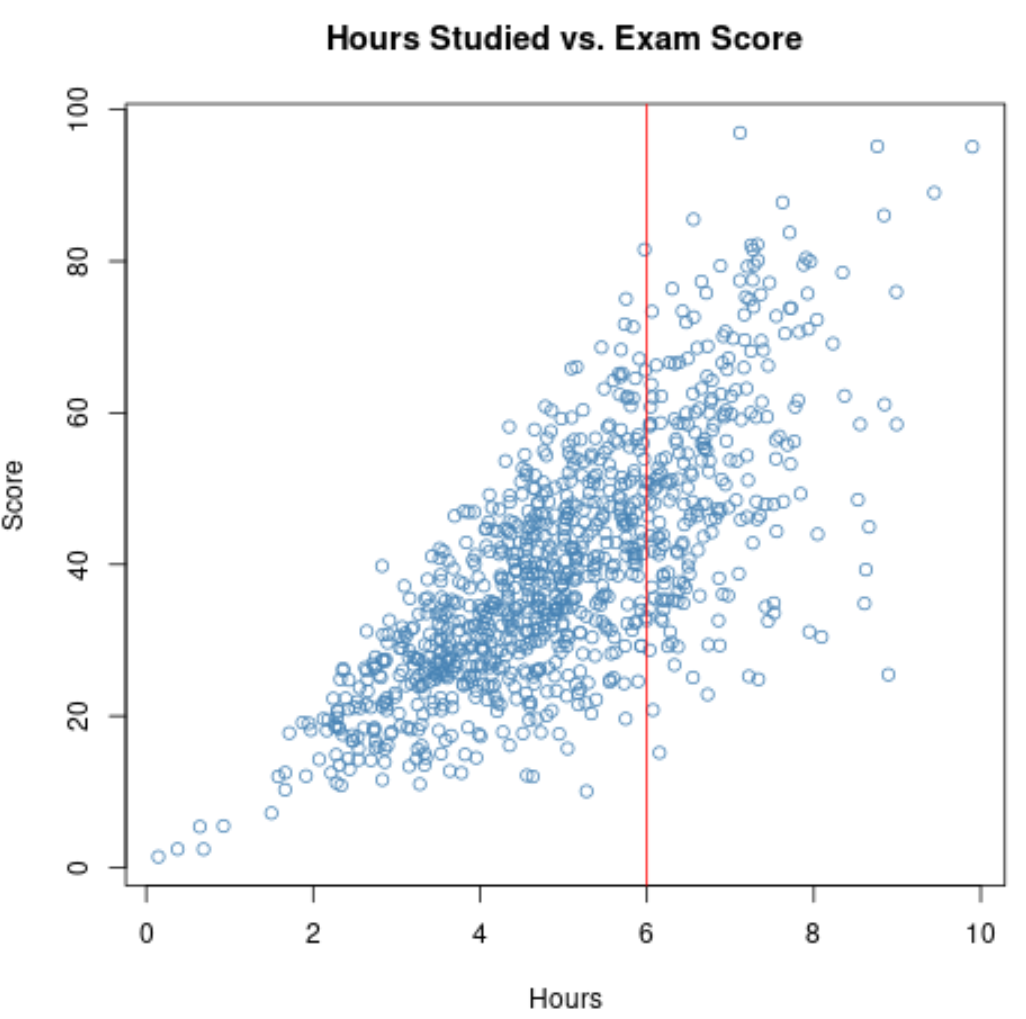
Wenn wir das Streudiagramm für den Bereich vergrößern, in dem die Stunden größer als 6 sind, sieht das Diagramm folgendermaßen aus:

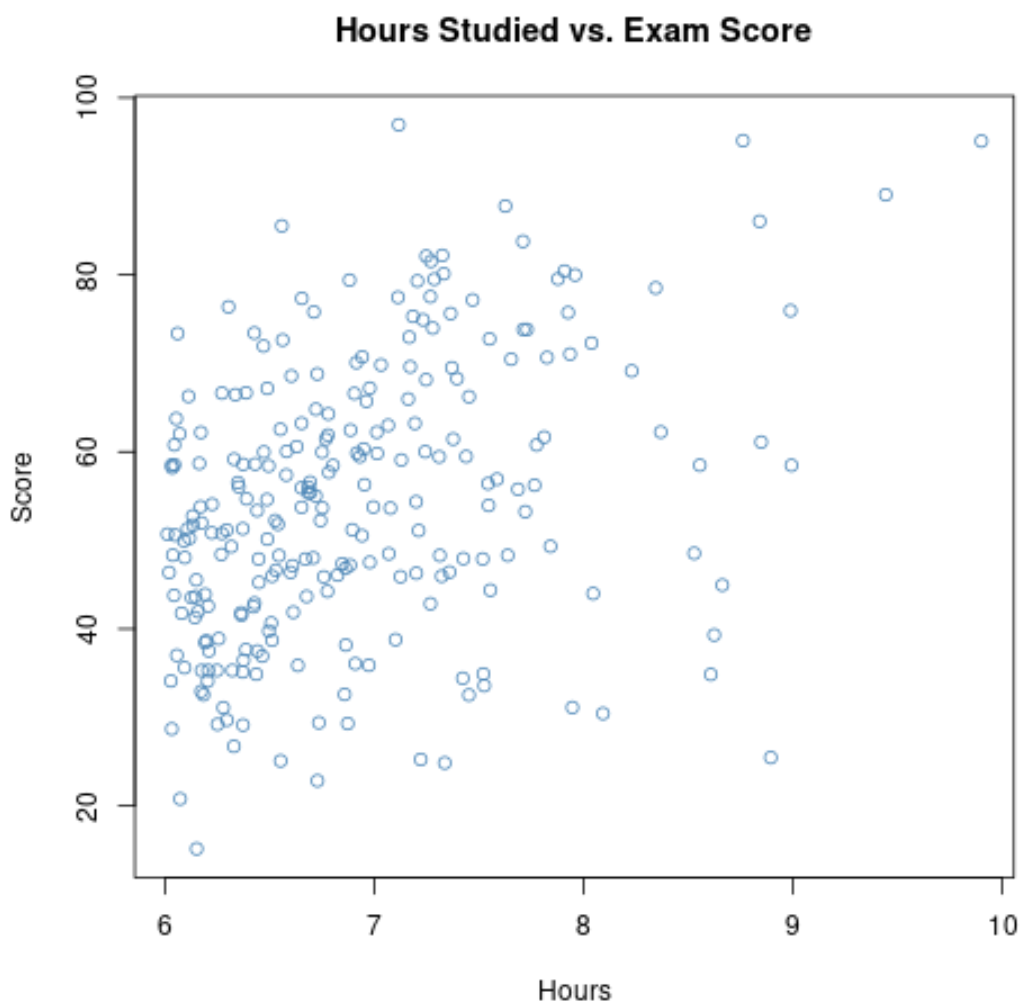
Die Korrelation zwischen den beiden Variablen in diesem Diagramm beträgt 0,37 , was deutlich niedriger als 0,73 ist.

Wenn wir also nur Daten zu den Lernstunden und den Prüfungsergebnissen für Studierende in Honours-Kursen sammeln würden, könnten wir annehmen, dass es einen schwachen Zusammenhang zwischen den Lernstunden und den Prüfungsergebnissen gibt.

Dieses Ergebnis wäre jedoch irreführend, da wir für eine der Variablen einen eingeschränkten Bereich verwendet haben.

Beispiele aus der Praxis für eingeschränkte Reichweite

Das Problem einer eingeschränkten Reichweite kann in der Praxis in vielen verschiedenen Forschungsstudien auftreten. Hier sind einige Beispiele:

1. Studien zu Hochleistungssportlern . Forscher könnten daran interessiert sein, zu untersuchen, ob ein bestimmtes Trainingsprogramm mehr Muskelmasse produziert als ein bestimmtes Standardprogramm.

Wenn Forscher nur Daten zu Spitzensportlern sammeln, ist es wahrscheinlich, dass diese Athleten alle bereits über eine hohe Muskelmasse verfügen. Es steht daher nur ein enger Wertebereich zur Verfügung, um den Zusammenhang zwischen Trainingsprogramm und erzeugter Muskelmasse zu berechnen.

2. Studien leistungsstarker Studierender. Forscher möchten möglicherweise untersuchen, ob sich ein bestimmtes Nachhilfeprogramm positiv auf die Noten auswirkt. Schüler, die ihre Noten verbessern und am Nachhilfeprogramm teilnehmen möchten, können von Natur aus bereits leistungsstarke Schüler sein.

Daher besteht möglicherweise nicht viel Raum für Verbesserungen bei den Noten dieser Schüler. Wenn Forscher die Korrelation zwischen den im Nachhilfeprogramm verbrachten Stunden und der daraus resultierenden Notenverbesserung berechnen, wird die tatsächliche Korrelation möglicherweise unterschätzt, da der Spielraum für Notenverbesserungen eingeschränkt wurde.

So berücksichtigen Sie eingeschränkte Bereiche

Eine beliebte Methode zur Berücksichtigung eingeschränkter Bereiche ist der Thorndike-Fall 2 , eine Formel, die vom Psychometriker Robert L. Thorndike entwickelt wurde.

Diese Formel liefert eine Schätzung der wahren Korrelation zwischen zwei Variablen und verwendet die folgende Berechnung:

Echte Korrelation = √(1-(SD ² _{y eingeschränkt} -SD ² _{y uneingeschränkt} )) * (1-r ² _{eingeschränkt} )

Gold:

• SD ² _{eingeschränkt y} : Die quadratische Standardabweichung der verfügbaren Daten zur Antwortvariablen y.
• _{Uneingeschränkte} SD ² Jahre: Die bekannte quadratische Standardabweichung der Antwortvariablen für die Grundgesamtheit.
• r ² _{eingeschränkt} : Die quadratische Korrelation der verfügbaren eingeschränkten Daten.

Es hat sich gezeigt, dass diese Formel wirksam ist, um unvoreingenommene Schätzungen der wahren Korrelation zwischen zwei Variablen zu erstellen, wenn eine der Variablen unter einem eingeschränkten Bereich leidet.

Beachten Sie, dass Sie zur Verwendung dieser Formel eine Schätzung der wahren Populationsstandardabweichung für die Antwortvariable benötigen.