Relative frequenz

In diesem Artikel erfahren Sie, was die relative Häufigkeit in der Statistik ist, wie Sie die relative Häufigkeit ermitteln und zwei Schritt-für-Schritt-Übungen zur relativen Häufigkeit lösen.

Was ist relative Häufigkeit?

In der Statistik ist die relative Häufigkeit ein Maß, das angibt, wie oft ein Wert in einer Datenstichprobe als Anteil oder Prozentsatz vorkommt. Genauer gesagt ist die relative Häufigkeit gleich der absoluten Häufigkeit dividiert durch die Gesamtzahl der Daten.

Wenn beispielsweise die absolute Häufigkeit eines Werts 15 beträgt und es insgesamt 100 Datenpunkte gibt, beträgt die relative Häufigkeit dieses Werts 0,15 (15/100=0,15).

Im Allgemeinen wird das Symbol h _i verwendet, um die relative Häufigkeit darzustellen. Obwohl es in der statistischen Gemeinschaft noch keinen Konsens gibt, können Sie die relative Häufigkeit durch ein anderes Symbol darstellen.

So berechnen Sie die relative Häufigkeit

Die relative Häufigkeit ist gleich der absoluten Häufigkeit dividiert durch die Gesamtzahl der Daten. Um die relative Häufigkeit zu berechnen, müssen Sie daher zunächst die absolute Häufigkeit ermitteln und diese dann durch die Gesamtzahl der Beobachtungen dividieren.

Die Formel für die relative Häufigkeit lautet also wie folgt:

Gold:

• 

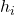
  ist die relative Häufigkeit.

• 

  ist die absolute Häufigkeit.

• 

  ist die Gesamtzahl der Daten.

Um hingegen die relative Häufigkeit in Prozent , also die relative Häufigkeit in Prozent, zu berechnen, multiplizieren Sie einfach die vorherige Formel mit 100:

Beispiele für relative Häufigkeit

Nachdem Sie die Definition der relativen Häufigkeit kennengelernt haben, finden Sie unten zwei Beispiele aus der Praxis, damit Sie sehen können, wie diese Art von Häufigkeit berechnet wird. Im ersten Beispiel wird die relative Häufigkeit einer diskreten Variablen bestimmt und im zweiten Beispiel einer kontinuierlichen Variablen.

Beispiel 1: diskrete Variable

• Die im Fach Statistik in einer Klasse mit 30 Schülern erzielten Noten lauten wie folgt. Wie groß ist die relative Häufigkeit jeder Note?

Die Variable in dieser Übung ist diskret, da die Daten nur ganze Zahlen sein können; Daher besteht keine Notwendigkeit, die Daten in Intervallen zu gruppieren.

Um die relative Häufigkeit zu ermitteln, müssen wir zunächst die absolute Häufigkeit bestimmen. Also erstellen wir eine Häufigkeitstabelle und berechnen die absolute Häufigkeit für jeden unterschiedlichen Wert:

Nachdem wir nun die absolute Häufigkeit berechnet haben, können wir die relative Häufigkeit berechnen. Teilen Sie dazu einfach jede absolute Häufigkeit durch die Gesamtzahl der Daten (30):

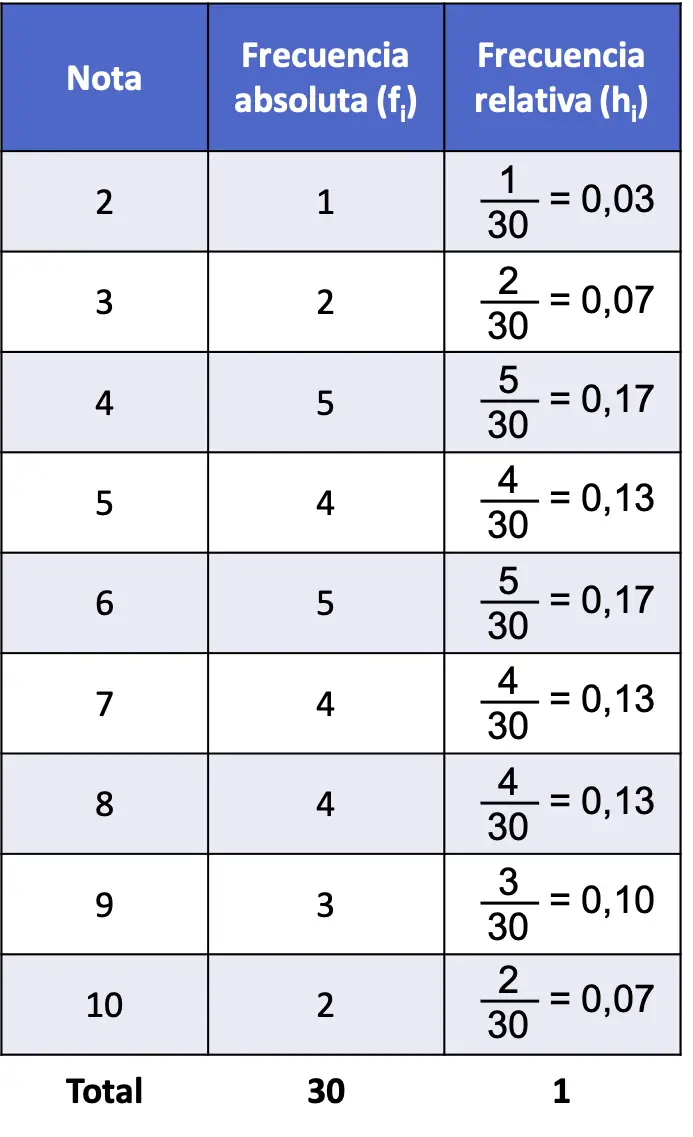
Die Häufigkeitstabelle des Problems mit absoluter Häufigkeit und relativer Häufigkeit lautet also wie folgt:

Beachten Sie, dass die Summe aller relativen Häufigkeiten immer 1 ergibt, andernfalls bedeutet dies, dass einige Berechnungen falsch sind.

Beispiel 2: kontinuierliche Variable

• Die Körpergröße von 20 Personen wurde gemessen und die unten aufgeführten Ergebnisse erzielt. Teilen Sie die Daten in Intervalle auf und ermitteln Sie die relative Häufigkeit jedes Intervalls.

Die Daten in dieser statistischen Stichprobe gehören zu einer kontinuierlichen Variablen, da sie dezimal sind und die Variable daher jeden beliebigen Wert annehmen kann. Bevor wir also die Häufigkeitsberechnungen durchführen, gruppieren wir die Daten zunächst in Intervalle mit einer Amplitude von 10 Zehnteln.

Als nächstes erstellen wir eine Häufigkeitstabelle mit der absoluten Häufigkeit jedes Intervalls:

Und sobald wir die absolute Häufigkeit ermittelt haben, können wir die relative Häufigkeit jedes Intervalls ermitteln, indem wir seine absolute Häufigkeit durch die Gesamtzahl der Daten (20) dividieren:

Kumulierte relative Häufigkeit

Wie der Name schon sagt, handelt es sich bei der kumulativen relativen Häufigkeit um eine andere Häufigkeitsart, die in der Statistik verwendet und aus der relativen Häufigkeit berechnet wird.

Genauer gesagt ist die kumulative relative Häufigkeit eines Werts gleich der Summe der relativen Häufigkeit des Werts selbst plus der relativen Häufigkeit aller kleineren Werte.

Damit Sie sehen können, wie die kumulative relative Häufigkeit ermittelt wird, wurde die kumulative relative Häufigkeit des Datensatzes im ersten Beispiel unten berechnet: