So berechnen sie das odds ratio und das relative risiko in excel

Wir verwenden häufig das Quotenverhältnis und das relative Risiko , wenn wir eine Analyse an einer 2×2-Tabelle durchführen, die das folgende Format hat:

Das Odds Ratio gibt uns das Verhältnis zwischen der Wahrscheinlichkeit des Eintretens eines Ereignisses in einer Behandlungsgruppe und der Wahrscheinlichkeit des Eintretens eines Ereignisses in einer Kontrollgruppe an. Es wird wie folgt berechnet:

Quotenverhältnis = (A*D) / (B*C)

Das relative Risiko gibt uns das Verhältnis zwischen der Wahrscheinlichkeit, dass ein Ereignis in einer Behandlungsgruppe auftritt, und der Wahrscheinlichkeit, dass ein Ereignis in einer Kontrollgruppe auftritt, an. Es wird wie folgt berechnet:

Relatives Risiko = [A/(A+B)] / [C/(C+D)]

In diesem Tutorial wird erklärt, wie Sie Quotenverhältnisse und relatives Risiko in Excel berechnen.

So berechnen Sie das Odds Ratio und das relative Risiko

Nehmen wir an, 50 Basketballspieler nutzen ein neues Trainingsprogramm und 50 Spieler nutzen ein altes Trainingsprogramm. Am Ende des Programms testen wir jeden Spieler, um zu sehen, ob er einen bestimmten Fähigkeitstest besteht.

Die folgende Tabelle zeigt die Anzahl der Spieler, die bestanden und nicht bestanden haben, basierend auf dem von ihnen verwendeten Programm:

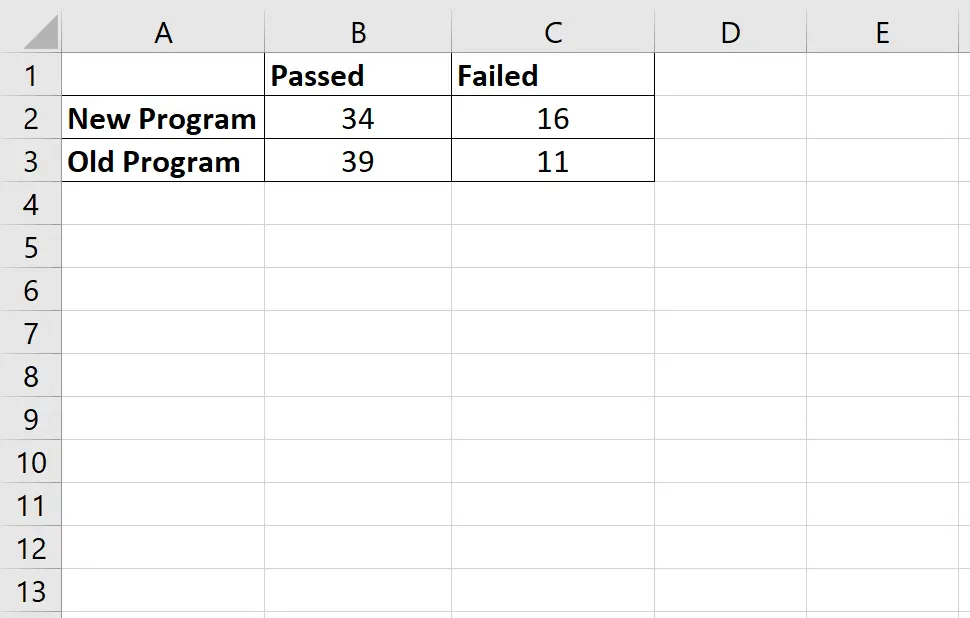
Das Quotenverhältnis wird wie folgt berechnet: (34*11) / (16*39) = 0,599

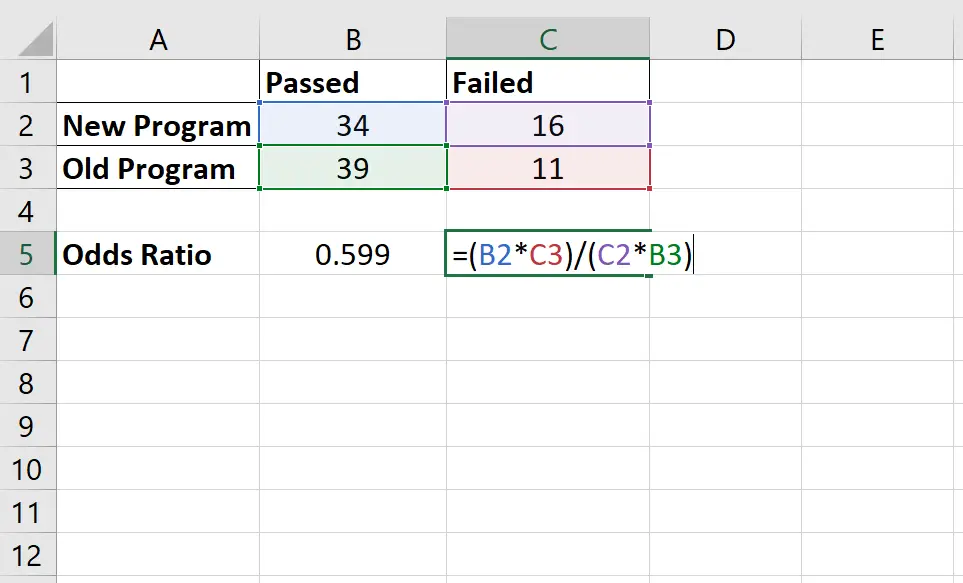
Wir würden dies so interpretieren, dass die Chancen, dass ein Spieler den Test mit dem neuen Programm besteht, nur 0,599-mal höher sind als die Chancen eines Spielers, den Test mit dem alten Programm zu bestehen.

Mit anderen Worten: Die Chancen, dass ein Spieler die Prüfung besteht, sinken dank des neuen Programms sogar um 40,1 %.

Das relative Risiko berechnet sich wie folgt: [34/(34+16)] / [39/(39+11)] = 0,872

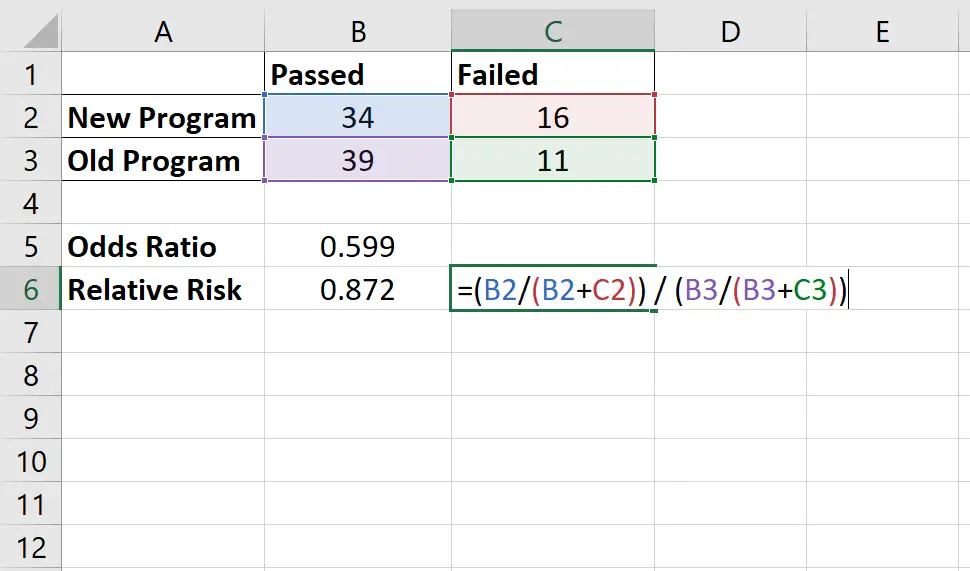
Wir würden dies so interpretieren, dass das Verhältnis zwischen der Wahrscheinlichkeit, dass ein Spieler den Test mit dem neuen Programm und dem alten Programm besteht, 0,872 beträgt.

Da dieser Wert kleiner als 1 ist, deutet dies darauf hin, dass die Erfolgswahrscheinlichkeit im neuen Programm tatsächlich geringer ist als im alten Programm.

Wir könnten dies auch sehen, indem wir direkt die Wahrscheinlichkeit berechnen, dass ein Spieler unter jedem Programm passt:

Erfolgswahrscheinlichkeit im Rahmen des neuen Programms = 34/50 = 68 %

Erfolgswahrscheinlichkeit im alten Programm = 39/50 = 78 %

So berechnen Sie Konfidenzintervalle

Nachdem wir das Odds Ratio und das relative Risiko berechnet haben, könnten wir auch daran interessiert sein, die Konfidenzintervalle für diese beiden Maße zu berechnen.

Ein 95 %-Konfidenzintervall für das Odds Ratio kann mit der folgenden Formel berechnet werden:

95 % KI für Odds Ratio = [ e^(ln(OR) – 1,96*SE(ln(OR))), e^(ln(OR) – 1,96*SE(ln(OR) )) ]

wobei SE(ln(OR)) =√ 1/A + 1/B + 1/C + 1/D

Das 95 %-KI für das Odds Ratio betrug (0,245; 1,467) . Das Bild unten zeigt die Formel, die wir zur Berechnung dieses Konfidenzintervalls verwendet haben:

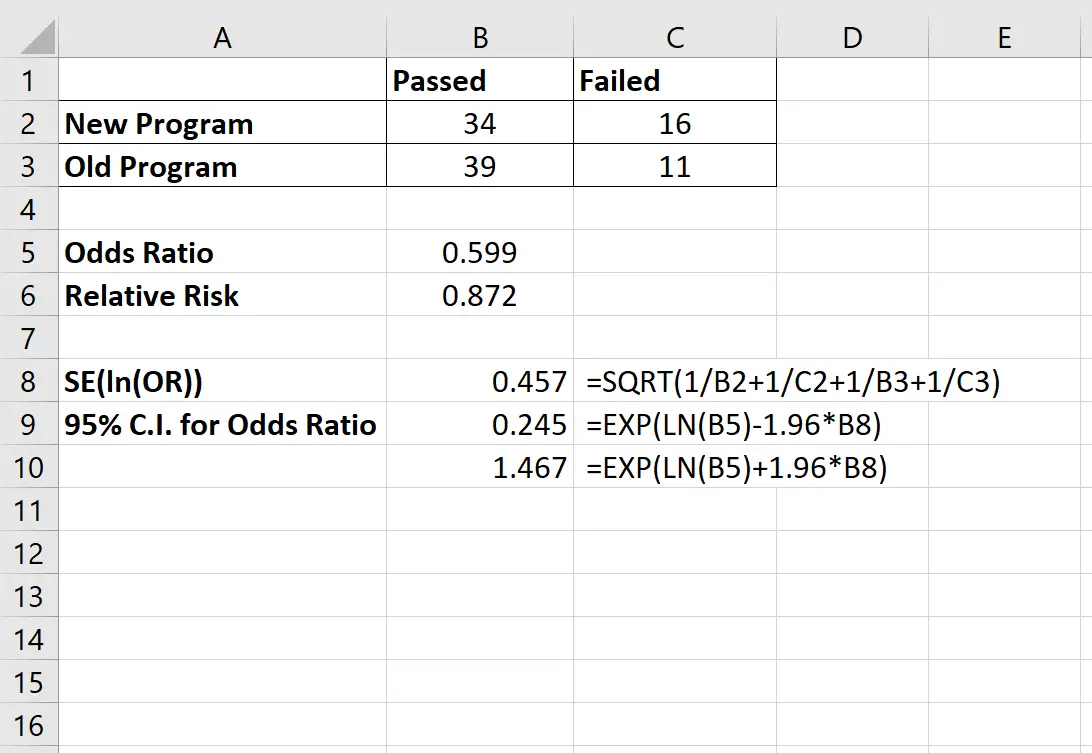
Ein 95 %-Konfidenzintervall für das relative Risiko kann mit der folgenden Formel berechnet werden:

95 %-KI für relatives Risiko = exp(ln(RR) – 1,96*SE(ln(RR))) bis exp(ln(RR) – 1,96*SE(ln(RR)))

wobei SE(ln(RR)) =√ 1/A + 1/C – 1/(A+B) – 1/(C+D)

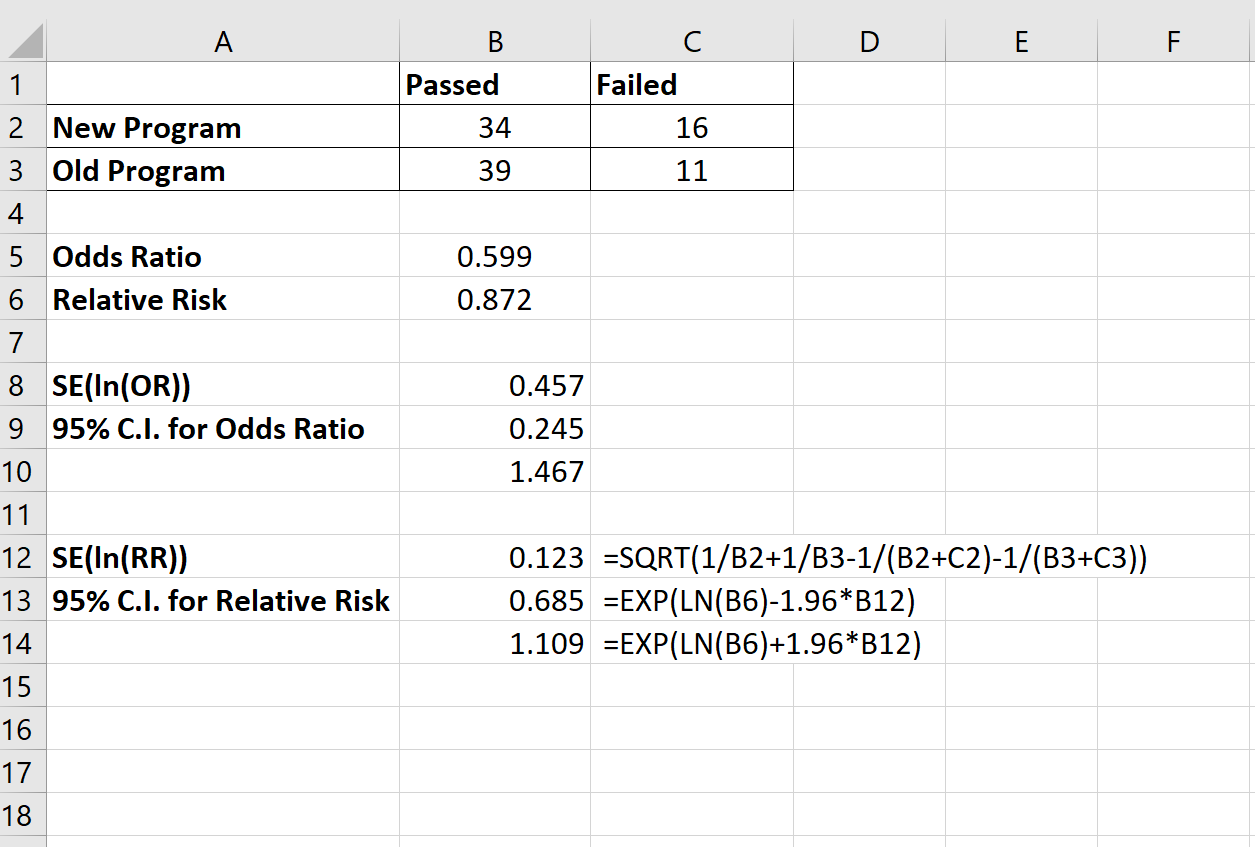
Das 95 %-KI für das relative Risiko betrug (0,685; 1,109) . Das Bild unten zeigt die Formel, die wir zur Berechnung dieses Konfidenzintervalls verwendet haben:

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zur Interpretation von Quotenverhältnissen und relativem Risiko:

Wie man Quotenverhältnisse interpretiert
Wie ist das relative Risiko zu interpretieren?