So berechnen sie ein konfidenzintervall für das relative risiko

Das relative Risiko wird häufig bei der Analyse einer 2×2-Tabelle berechnet, die das folgende Format hat:

Das relative Risiko gibt uns die Wahrscheinlichkeit an, mit der ein Ereignis in einer Behandlungsgruppe auftritt, verglichen mit der Wahrscheinlichkeit, dass ein Ereignis in einer Kontrollgruppe auftritt.

Es wird wie folgt berechnet:

• Relatives Risiko = [A/(A+B)] / [C/(C+D)]

Mit der folgenden Formel können wir dann ein Konfidenzintervall für das relative Risiko (RR) berechnen:

• CI weniger als 95 % = e ^{ln(RR) – 1,96√ 1/a + 1/c – 1/(a+b) – 1/(c+d)}
• CI größer als 95 % = e ^{ln(RR) + 1,96√ 1/a + 1/c – 1/(a+b) – 1/(c+d)}

Das folgende Beispiel zeigt, wie man in der Praxis ein relatives Risiko und ein entsprechendes Konfidenzintervall berechnet.

Beispiel: Berechnung eines Konfidenzintervalls für das relative Risiko

Angenommen, ein Basketballtrainer verwendet ein neues Trainingsprogramm, um zu sehen, ob es im Vergleich zu einem alten Trainingsprogramm die Anzahl der Spieler erhöht, die einen bestimmten Fähigkeitstest bestehen können.

Der Trainer rekrutiert 50 Spieler, um jedes Programm zu nutzen. Die folgende Tabelle zeigt die Anzahl der Spieler, die den Fähigkeitstest bestanden und nicht bestanden haben, basierend auf dem von ihnen verwendeten Programm:

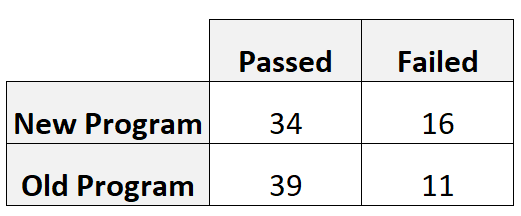
Das relative Risiko können wir wie folgt berechnen:

• Relatives Risiko = [A/(A+B)] / [C/(C+D)]
• Relatives Risiko = [34/(34+16)] / [39/(39+11)]
• Relatives Risiko = 0,8718

Wir interpretieren dies so, dass die Wahrscheinlichkeit, dass ein Spieler den Test mit dem neuen Programm besteht, nur 0,8718-mal so groß ist wie die Wahrscheinlichkeit, dass ein Spieler den Test mit dem alten Programm besteht.

Mit anderen Worten: Die Wahrscheinlichkeit, dass ein Spieler den Test besteht, wird durch den Einsatz des neuen Programms tatsächlich verringert.

Mithilfe der folgenden Formeln können wir dann das 95 %-Konfidenzintervall für das relative Risiko berechnen:

• KI unter 95 % = e ^{ln(.8718) – 1,96√ (1/34 + 1/39 – 1/(34+16) – 1/(39+11)} = 0,686
• KI größer als 95 % = e ^{ln(.8718) + 1,96√ (1/34 + 1/39 + 1/(34+16) – 1/(39+11)} = 1,109

Somit beträgt das 95 %-Konfidenzintervall für das relative Risiko [0,686, 1,109] .

Wir sind zu 95 % davon überzeugt, dass das tatsächliche relative Risiko zwischen dem neuen und dem alten Trainingsprogramm innerhalb dieses Intervalls liegt.

Da dieses Konfidenzintervall den Wert 1 enthält, ist es statistisch nicht signifikant.

Dies sollte sinnvoll sein, wenn Sie Folgendes berücksichtigen:

• Ein relatives Risiko größer als 1 würde bedeuten, dass die Wahrscheinlichkeit, dass ein Spieler den Test mit dem neuen Programm besteht, größer ist als die Wahrscheinlichkeit, dass ein Spieler den Test mit dem alten Programm besteht.
• Ein relatives Risiko kleiner als 1 würde bedeuten, dass die Wahrscheinlichkeit, dass ein Spieler den Test mit dem neuen Programm besteht, geringer ist als die Wahrscheinlichkeit, dass ein Spieler den Test mit dem alten Programm besteht.

Da unser 95 %-Konfidenzintervall für das relative Risiko den Wert 1 enthält, bedeutet dies, dass die Wahrscheinlichkeit, dass ein Spieler den Fähigkeitstest mit dem neuen Programm besteht, möglicherweise größer ist als die Wahrscheinlichkeit, dass derselbe Spieler den Test mit dem besteht neues Programm. altes Programm.

Zusätzliche Ressourcen

Die folgenden Tutorials bieten zusätzliche Informationen zu Quotenverhältnissen und relativem Risiko:

Wie man Quotenverhältnisse interpretiert
Wie ist das relative Risiko zu interpretieren?
So berechnen Sie das Odds Ratio und das relative Risiko in Excel