Wie groß ist die restlücke? (definition & #038; beispiel)

Die Restvarianz (manchmal auch „unerklärte Varianz“ genannt) bezieht sich auf die Varianz in einem Modell, die nicht durch die Modellvariablen erklärt werden kann.

Je höher die Restvarianz eines Modells ist, desto weniger kann das Modell die Variation in den Daten erklären.

Die Restvarianz erscheint in den Ergebnissen zweier unterschiedlicher statistischer Modelle:

1. ANOVA: Wird verwendet, um die Mittelwerte von drei oder mehr unabhängigen Gruppen zu vergleichen.

2. Regression: Wird zur Quantifizierung der Beziehung zwischen einer oder mehreren Prädiktorvariablen und einer Antwortvariablen verwendet.

Die folgenden Beispiele zeigen, wie die Restvarianz bei jeder dieser Methoden interpretiert wird.

Restvarianz in ANOVA-Modellen

Jedes Mal, wenn wir ein ANOVA-Modell („Varianzanalyse“) anpassen, erhalten wir eine ANOVA-Tabelle, die wie folgt aussieht:

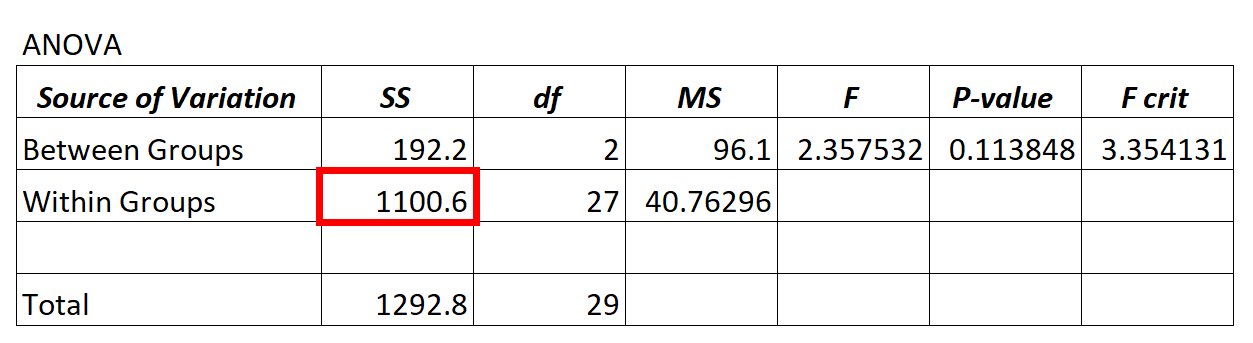
Der Restvarianzwert des ANOVA-Modells befindet sich in der SS-Spalte („Quadratsumme“) für die Variation innerhalb der Gruppe .

Dieser Wert wird auch „Summe der quadratischen Fehler“ genannt und wird nach folgender Formel berechnet:

Σ(X _ij – X _j ) ²

Gold:

• Σ : ein griechisches Symbol mit der Bedeutung „Summe“
• X _ij : die ^i-te Beobachtung der Gruppe j
• X _j : der Durchschnitt der Gruppe j

Im obigen ANOVA-Modell sehen wir, dass die Restvarianz 1100,6 beträgt.

Um festzustellen, ob diese Restvarianz „hoch“ ist, können wir die mittlere Summe der Quadrate innerhalb von Gruppen und die mittlere Summe der Quadrate zwischen Gruppen berechnen und das Verhältnis zwischen beiden ermitteln, das den Gesamt-F-Wert in der ANOVA-Tabelle ergibt.

• F = MS _{kommt herein} / MS _rein
• F = 96,1 / 40,76296
• F = 2,357

Der F-Wert in der ANOVA-Tabelle oben beträgt 2,357 und der entsprechende p-Wert beträgt 0,113848. Da dieser p-Wert nicht kleiner als α = 0,05 ist, haben wir keine ausreichenden Beweise, um die Nullhypothese abzulehnen.

Das bedeutet, dass uns keine ausreichenden Beweise dafür vorliegen, dass der mittlere Unterschied zwischen den Gruppen, die wir vergleichen, signifikant unterschiedlich ist.

Dies zeigt uns, dass die Restvarianz des ANOVA-Modells im Vergleich zu der Variation, die das Modell tatsächlich erklären kann, hoch ist.

Restvarianz in Regressionsmodellen

In einem Regressionsmodell ist die Restvarianz als Summe der Quadrate der Differenzen zwischen den vorhergesagten Datenpunkten und den beobachteten Datenpunkten definiert.

Es wird wie folgt berechnet:

Σ(ŷ _i – y _i ) ²

Gold:

• Σ : ein griechisches Symbol mit der Bedeutung „Summe“
• ŷ _i : Die vorhergesagten Datenpunkte
• y _i : Die beobachteten Datenpunkte

Wenn wir ein Regressionsmodell anpassen, erhalten wir normalerweise ein Ergebnis, das wie folgt aussieht:

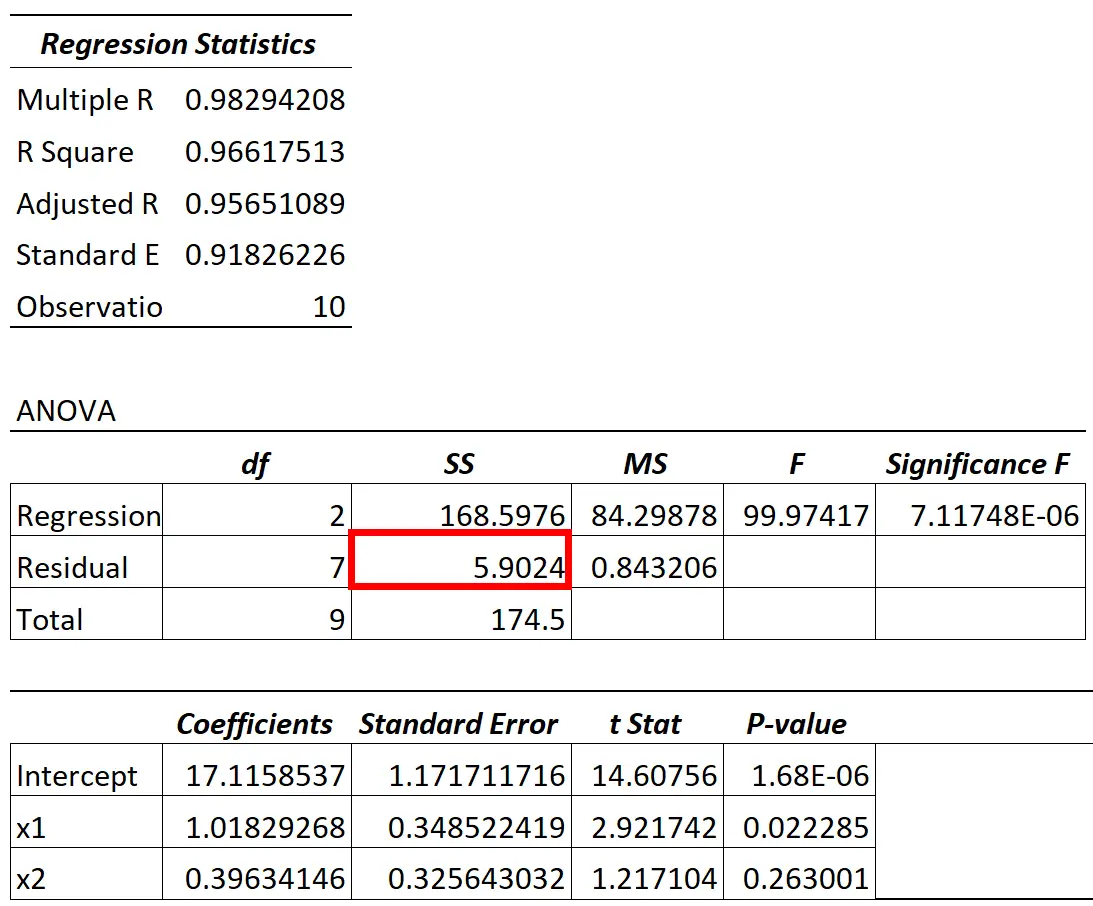
Der Restvarianzwert des ANOVA-Modells ist in der SS-Spalte („Quadratsumme“) für Restvariation zu finden.

Das Verhältnis der Restvariation zur Gesamtvariation im Modell gibt Auskunft über den Prozentsatz der Variation in der Antwortvariablen, der nicht durch die Prädiktorvariablen im Modell erklärt werden kann.

In der obigen Tabelle würden wir diesen Prozentsatz beispielsweise wie folgt berechnen:

• Unerklärte Variation = SS-Rest / SS-Gesamt
• Unerklärte Variation = 5,9024 / 174,5
• Unerklärte Variation = 0,0338

Dieser Wert kann auch mit der folgenden Formel berechnet werden:

• Unerklärte Variation = 1 – R ²
• Unerklärte Variation = 1 – 0,96617
• Unerklärte Variation = 0,0338

Der R-Quadrat-Wert des Modells gibt uns den Prozentsatz der Variation in der Antwortvariablen an, der durch die Prädiktorvariable erklärt werden kann.

Je geringer also die unerklärte Variation ist, desto besser ist ein Modell in der Lage, mithilfe der Prädiktorvariablen die Variation der Antwortvariablen zu erklären.

Zusätzliche Ressourcen

Was ist ein guter R-Quadrat-Wert?
So berechnen Sie das R-Quadrat in Excel
So berechnen Sie das R-Quadrat in R