So führen sie eine robuste regression in r durch (schritt für schritt)

Die robuste Regression ist eine Methode, die wir als Alternative zur gewöhnlichen Regression der kleinsten Quadrate verwenden können, wenn der Datensatz, mit dem wir arbeiten, Ausreißer oder einflussreiche Beobachtungen enthält.

Um eine robuste Regression in R durchzuführen, können wir die Funktion rlm() aus dem MASS- Paket verwenden, die die folgende Syntax verwendet:

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie eine robuste Regression in R für einen bestimmten Datensatz durchgeführt wird.

Schritt 1: Erstellen Sie die Daten

Erstellen wir zunächst einen gefälschten Datensatz, mit dem wir arbeiten können:

 #create data
df <- data. frame (x1=c(1, 3, 3, 4, 4, 6, 6, 8, 9, 3,
                      11, 16, 16, 18, 19, 20, 23, 23, 24, 25),
                 x2=c(7, 7, 4, 29, 13, 34, 17, 19, 20, 12,
                      25, 26, 26, 26, 27, 29, 30, 31, 31, 32),
                  y=c(17, 170, 19, 194, 24, 2, 25, 29, 30, 32,
                      44, 60, 61, 63, 63, 64, 61, 67, 59, 70))

#view first six rows of data
head(df)

  x1 x2 y
1 1 7 17
2 3 7 170
3 3 4 19
4 4 29 194
5 4 13 24
6 6 34 2

Schritt 2: Führen Sie eine gewöhnliche Regression der kleinsten Quadrate durch

Als Nächstes passen wir ein gewöhnliches Regressionsmodell der kleinsten Quadrate an und erstellen ein Diagramm der standardisierten Residuen .

In der Praxis betrachten wir häufig jedes standardisierte Residuum, dessen absoluter Wert größer als 3 ist, als Ausreißer.

 #fit ordinary least squares regression model
ols <- lm(y~x1+x2, data=df)

#create plot of y-values vs. standardized residuals
plot(df$y, rstandard(ols), ylab=' Standardized Residuals ', xlab=' y ') 
abline(h= 0 ) 

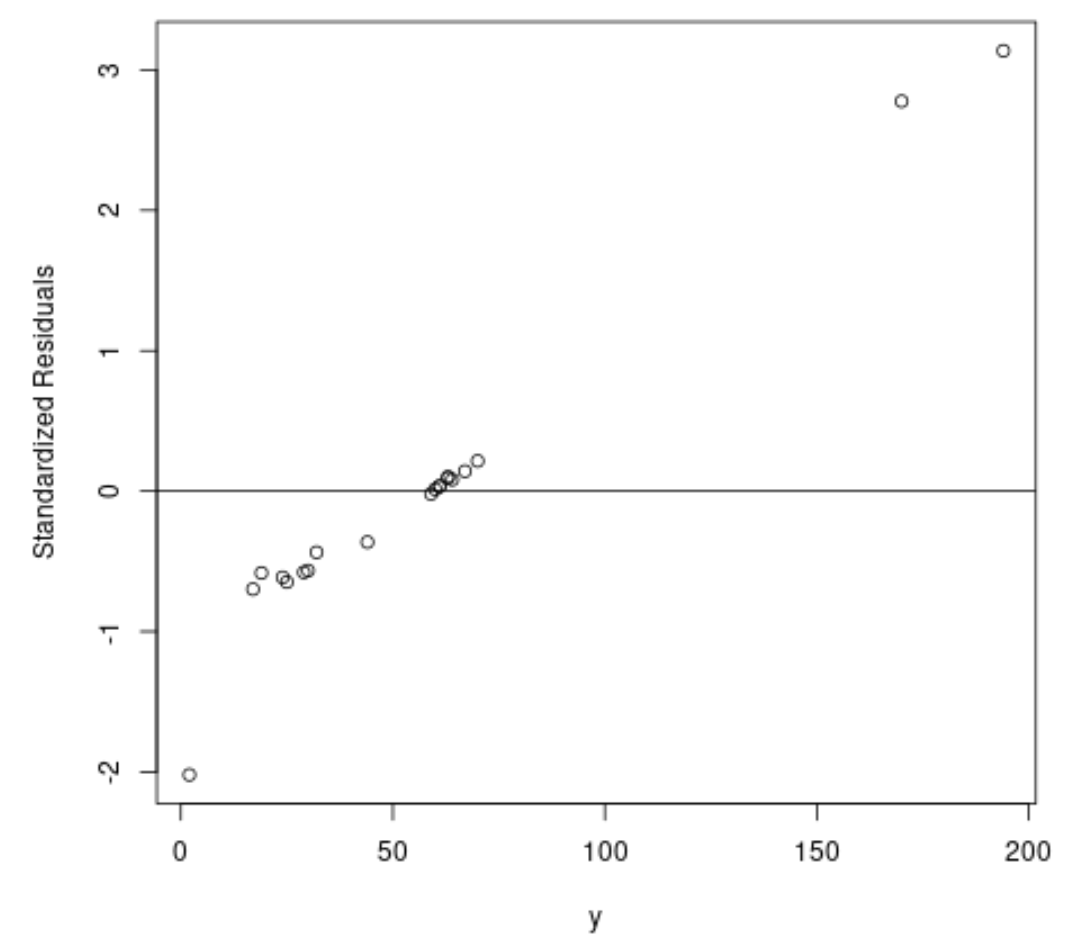
Aus der Grafik können wir ersehen, dass es zwei Beobachtungen mit standardisierten Residuen um 3 gibt.

Dies weist darauf hin, dass der Datensatz zwei potenzielle Ausreißer enthält und wir daher möglicherweise stattdessen von einer robusten Regression profitieren könnten.

Schritt 3: Führen Sie eine robuste Regression durch

Als nächstes verwenden wir die Funktion rlm(), um ein robustes Regressionsmodell anzupassen:

 library (MASS)

#fit robust regression model
robust <- rlm(y~x1+x2, data=df)

Um festzustellen, ob dieses robuste Regressionsmodell im Vergleich zum OLS-Modell eine bessere Anpassung an die Daten bietet, können wir den verbleibenden Standardfehler jedes Modells berechnen.

Der Reststandardfehler (RSE) ist eine Möglichkeit, die Standardabweichung der Residuen in einem Regressionsmodell zu messen. Je niedriger der CSR-Wert, desto besser kann ein Modell die Daten anpassen.

Der folgende Code zeigt, wie der RSE für jedes Modell berechnet wird:

 #find residual standard error of ols model
summary(ols)$sigma

[1] 49.41848

#find residual standard error of ols model
summary(robust)$sigma

[1] 9.369349

Wir können sehen, dass der RSE des robusten Regressionsmodells viel niedriger ist als der des gewöhnlichen Regressionsmodells der kleinsten Quadrate, was uns sagt, dass das robuste Regressionsmodell eine bessere Anpassung an die Daten bietet.

Zusätzliche Ressourcen

So führen Sie eine einfache lineare Regression in R durch
So führen Sie eine multiple lineare Regression in R durch
So führen Sie eine Polynomregression in R durch