Was sind residuen in der statistik?

Ein Residuum ist die Differenz zwischen einem beobachteten Wert und einem vorhergesagten Wert inder Regressionsanalyse .

Es wird wie folgt berechnet:

Residuum = Beobachteter Wert – Vorhergesagter Wert

Denken Sie daran, dass das Ziel der linearen Regression darin besteht, die Beziehung zwischen einer oder mehreren Prädiktorvariablen und einer Antwortvariablen zu quantifizieren. Zu diesem Zweck findet die lineare Regression die Linie, die am besten zu den Daten „passt“, die sogenannte Regressionslinie der kleinsten Quadrate .

Diese Linie erzeugt eine Vorhersage für jede Beobachtung im Datensatz, es ist jedoch unwahrscheinlich, dass die von der Regressionslinie getroffene Vorhersage genau mit dem beobachteten Wert übereinstimmt.

Der Unterschied zwischen der Vorhersage und dem beobachteten Wert ist das Residuum. Wenn wir die beobachteten Werte grafisch darstellen und die angepasste Regressionslinie überlagern, wären die Residuen für jede Beobachtung der vertikale Abstand zwischen der Beobachtung und der Regressionslinie:

Eine Beobachtung hat ein positives Residuum , wenn ihr Wert größer ist als der durch die Regressionsgerade vorhergesagte Wert.

Umgekehrt hat eine Beobachtung ein negatives Residuum , wenn ihr Wert kleiner ist als der durch die Regressionsgerade vorhergesagte Wert.

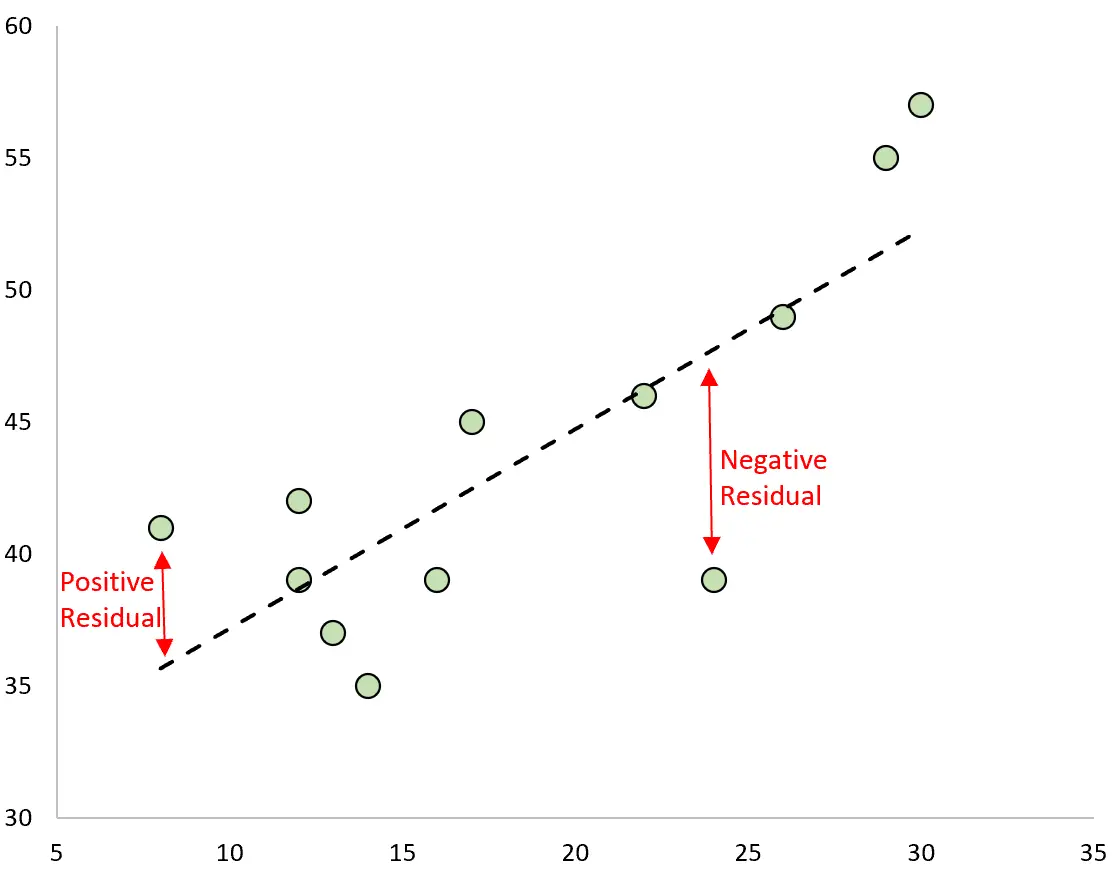
Einige Beobachtungen haben positive Residuen, während andere negative Residuen haben, aber alle Residuen ergeben in der Summe Null .

Beispiel für die Berechnung von Residuen

Angenommen, wir haben den folgenden Datensatz mit insgesamt 12 Beobachtungen:

Wenn wir Statistiksoftware (wie R , Excel , Python , Stata usw.) verwenden, um eine lineare Regressionslinie an diesen Datensatz anzupassen, werden wir feststellen, dass die am besten geeignete Linie wie folgt aussieht:

y = 29,63 + 0,7553x

Mithilfe dieser Linie können wir den vorhergesagten Wert für jeden Y-Wert basierend auf dem Wert von X berechnen. Der vorhergesagte Wert der ersten Beobachtung wäre beispielsweise:

y = 29,63 + 0,7553*(8) = 35,67

Wir können dann das Residuum für diese Beobachtung wie folgt berechnen:

Residuum = Beobachteter Wert – Vorhergesagter Wert = 41 – 35,67 = 5,33

Wir können diesen Vorgang wiederholen, um das Residuum für jede Beobachtung zu ermitteln:

Wenn wir ein Streudiagramm erstellen, um die Beobachtungen mit der angepassten Regressionslinie zu visualisieren, werden wir sehen, dass einige der Beobachtungen über der Linie liegen, während andere unter der Linie liegen:

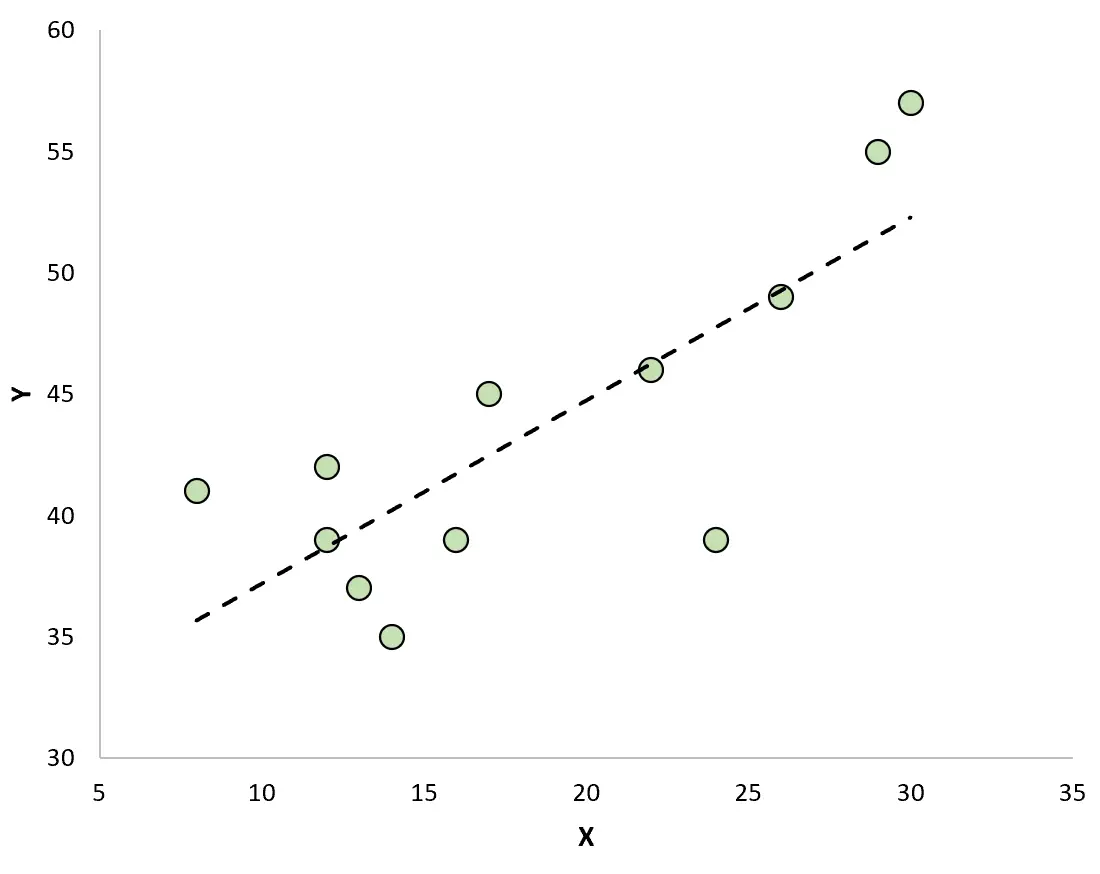
Eigenschaften von Rückständen

Rückstände haben folgende Eigenschaften:

• Jede Beobachtung in einem Datensatz hat ein entsprechendes Residuum. Wenn ein Datensatz also insgesamt 100 Beobachtungen enthält, erzeugt das Modell 100 vorhergesagte Werte, was insgesamt 100 Residuen ergibt.
• Die Summe aller Residuen ist Null.
• Der Durchschnittswert der Residuen ist Null.

Wie werden Rückstände in der Praxis verwendet?

In der Praxis werden Residuen aus drei verschiedenen Gründen bei der Regression verwendet:

1. Bewerten Sie die Angemessenheit des Modells.

Sobald wir eine angepasste Regressionslinie erstellt haben, können wir die Residualsumme der Quadrate (RSS) berechnen, die die Summe aller quadrierten Residuen ist. Je niedriger der RSS, desto besser passt das Regressionsmodell an die Daten.

2. Überprüfen Sie die Normalitätsannahme.

Eine der wichtigsten Annahmen der linearen Regression ist, dass die Residuen normalverteilt sind.

Um diese Hypothese zu testen, können wir ein QQ-Diagramm erstellen. Dabei handelt es sich um eine Art Diagramm, mit dem wir bestimmen können, ob die Residuen eines Modells einer Normalverteilung folgen oder nicht.

Wenn die Punkte auf dem Diagramm ungefähr eine gerade Diagonale bilden, ist die Normalitätsannahme erfüllt.

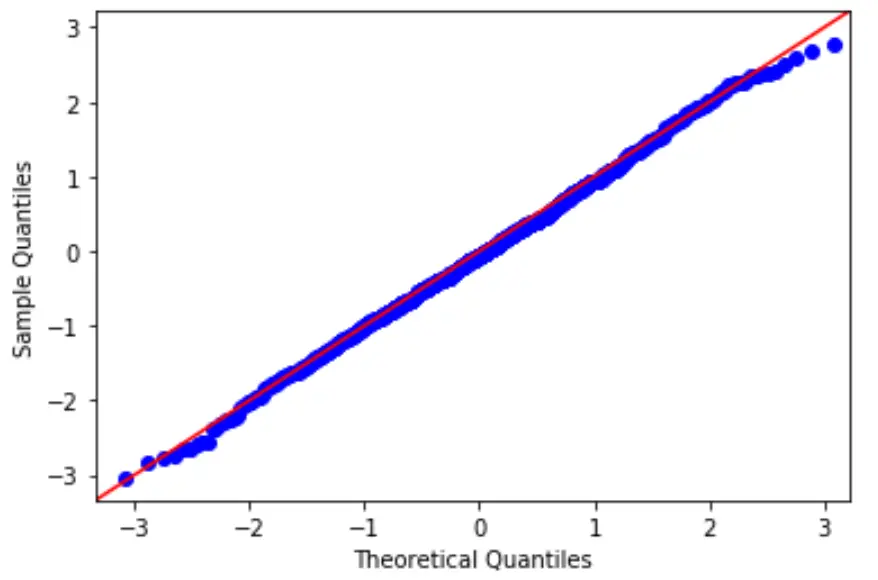
3. Überprüfen Sie die Homoskedastizitätsannahme.

Eine weitere wichtige Annahme der linearen Regression besteht darin, dass die Residuen auf jeder Ebene von x eine konstante Varianz aufweisen. Dies nennt man Homoskedastizität. Wenn dies nicht der Fall ist, leiden die Residuen unter Heteroskedastizität .

Um zu überprüfen, ob diese Annahme erfüllt ist, können wir ein Residuendiagramm erstellen, bei dem es sich um ein Streudiagramm handelt, das die Residuen im Vergleich zu den vorhergesagten Werten des Modells zeigt.

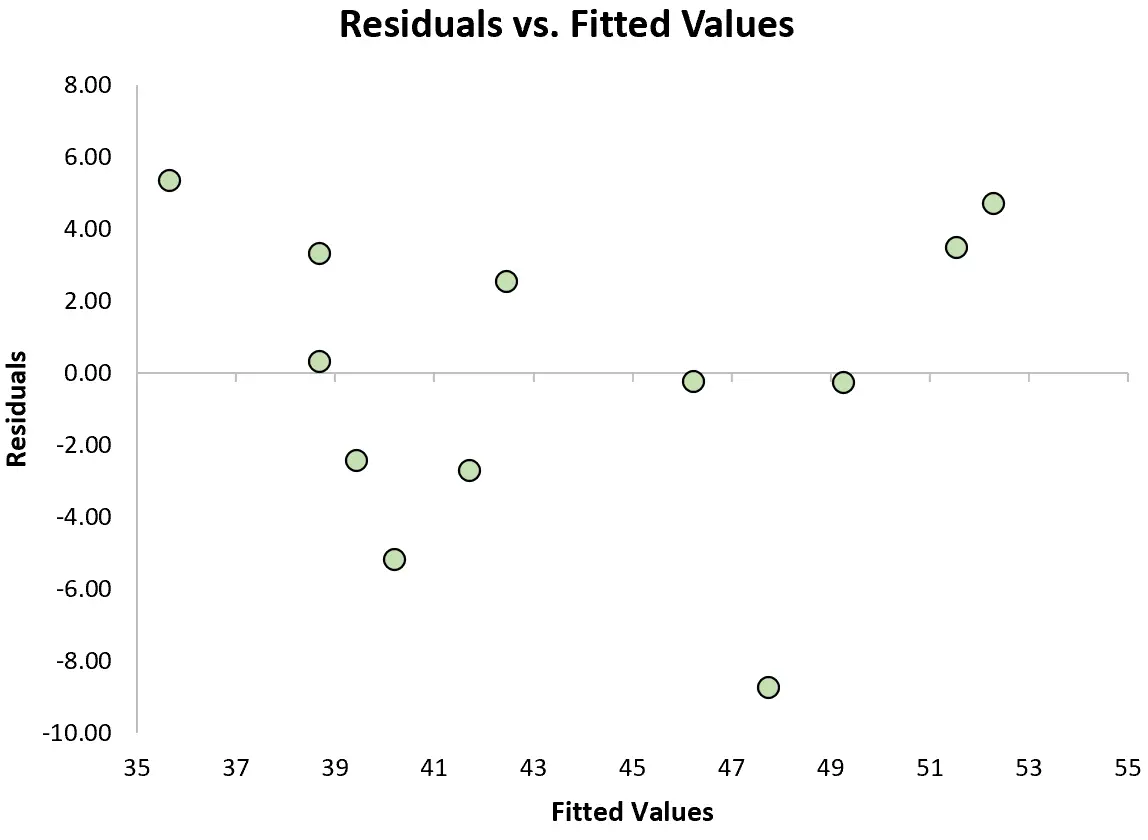
Wenn die Residuen in der Grafik annähernd gleichmäßig um Null verteilt sind und kein klarer Trend erkennbar ist, dann sagen wir im Allgemeinen, dass die Annahme der Homoskedastizität erfüllt ist.

Zusätzliche Ressourcen

Einführung in die einfache lineare Regression
Einführung in die multiple lineare Regression
Die vier Annahmen der linearen Regression
So erstellen Sie ein Residuendiagramm in Excel