So berechnen sie konfidenzintervalle in sas

EinKonfidenzintervall ist ein Wertebereich, der wahrscheinlich einen Populationsparameter mit einem bestimmten Konfidenzniveau enthält.

In diesem Tutorial wird erklärt, wie die folgenden Konfidenzintervalle in R berechnet werden:

1. Konfidenzintervall für einen Grundgesamtheitsmittelwert

2. Konfidenzintervall für einen Unterschied in den Mittelwerten der Grundgesamtheit

Lass uns gehen!

Beispiel 1: Konfidenzintervall für den Grundgesamtheitsmittelwert in SAS

Angenommen, wir haben den folgenden Datensatz, der die Höhe (in Zoll) einer Zufallsstichprobe von 12 Pflanzen enthält, die alle derselben Art angehören:

 /*create dataset*/
data my_data;
    inputHeight ;
    datalines ;
14
14
16
13
12
17
15
14
15
13
15
14
;
run ;

/*view dataset*/
proc print data =my_data; 

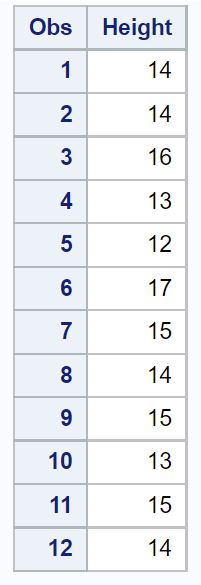
Angenommen, wir möchten ein Konfidenzniveau von 95 % für die tatsächliche durchschnittliche Populationsgröße dieser Art berechnen.

Wir können dazu den folgenden Code in SAS verwenden:

 /*generate 95% confidence interval for population mean*/
proc ttest data =my_data alpha = 0.05 ;
    varHeight ;
run ;

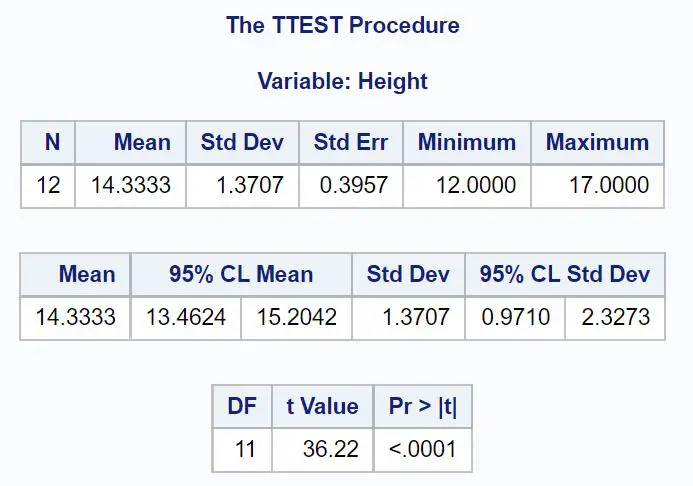
Der Mittelwert gibt den Stichprobenmittelwert an, und Werte unter 95 % CL-Mittelwert zeigen das 95 %-Konfidenzintervall für den Grundgesamtheitsmittelwert an.

Aus den Ergebnissen können wir ersehen, dass das 95 %-Konfidenzintervall für das durchschnittliche Pflanzengewicht dieser Population [13,4624 Zoll, 15,2042 Zoll] beträgt.

Beispiel 2: Konfidenzintervall für die Differenz der Grundgesamtheitsmittelwerte in SAS

Angenommen, wir haben den folgenden Datensatz, der die Höhe (in Zoll) einer Zufallsstichprobe von Pflanzen enthält, die zu zwei verschiedenen Arten gehören:

 /*create dataset*/
data my_data2;
    input Species $Height;
    datalines ;
At 14
At 14
At 16
At 13
AT 12
At 17
At 15
At 14
At 15
At 13
B15
B14
B 19
B 19
B17
B 18
B20
B 19
B17
B15
;
run ;

/*view dataset*/
proc print data =my_data2; 

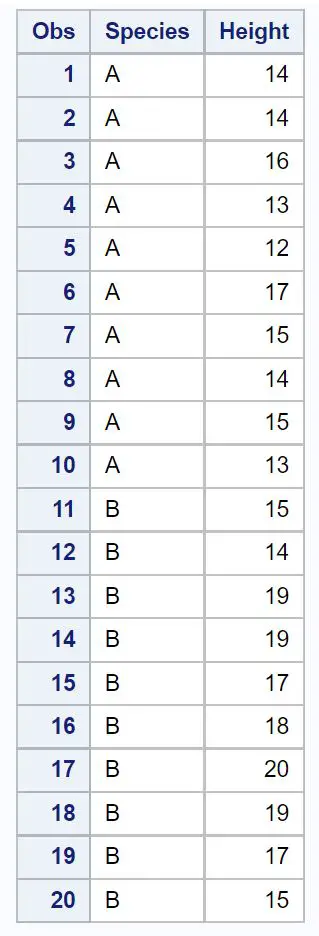
Angenommen, wir möchten ein 95-prozentiges Konfidenzniveau für den Unterschied in der durchschnittlichen Populationsgröße zwischen Art A und Art B berechnen.

Wir können dazu den folgenden Code in SAS verwenden:

 /*sort data by Species to ensure confidence interval is calculated correctly*/
proc sort data =my_data2;
    by Species;
run ;

/*generate 95% confidence interval for difference in population means*/
proc ttest data =my_data2 alpha = 0.05 ;
    class Species;
    varHeight ;
run ;

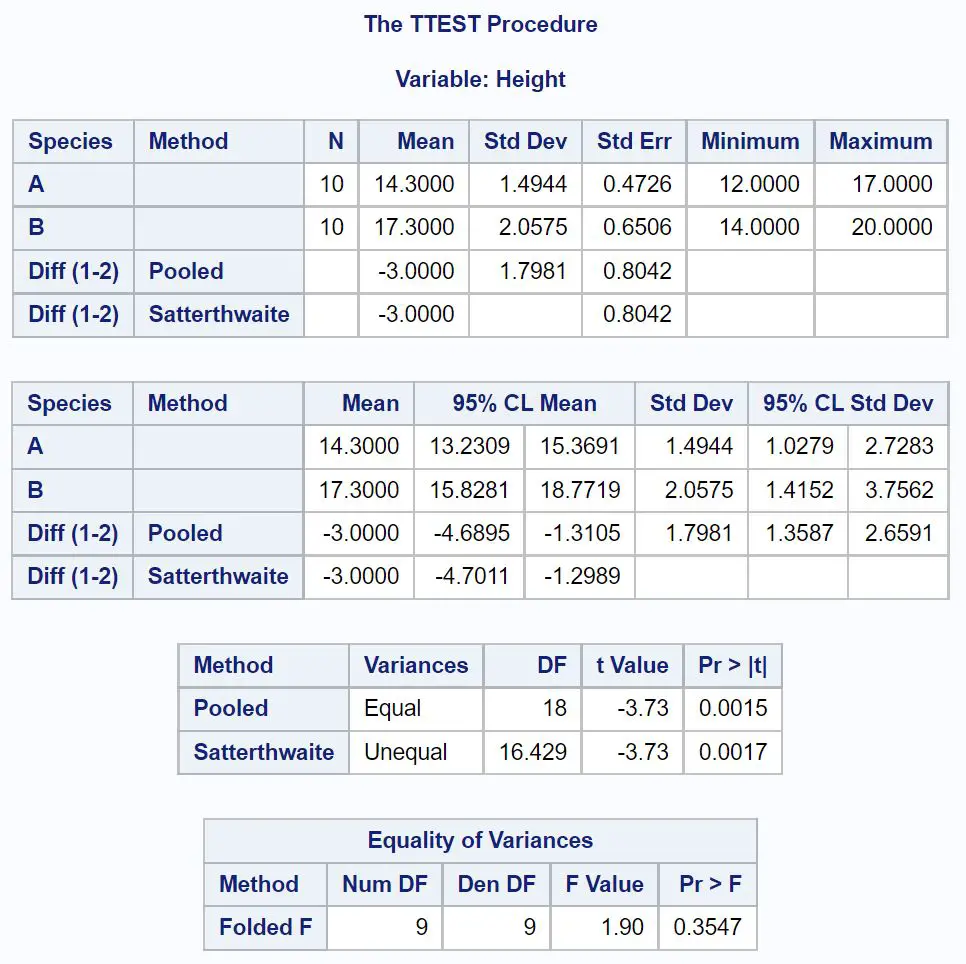
Die erste Tabelle, die wir uns im Ergebnis ansehen müssen, ist Varianzgleichheit . Sie testet, ob die Varianz zwischen den einzelnen Stichproben gleich ist oder nicht.

Da der p-Wert in dieser Tabelle nicht weniger als 0,05 beträgt, können wir davon ausgehen, dass die Unterschiede zwischen den beiden Gruppen gleich sind.

Wir können uns also die Linie ansehen, die die gepoolte Varianz verwendet, um das 95 %-Konfidenzintervall für die Differenz in den Mittelwerten der Grundgesamtheit zu ermitteln.

Aus dem Ergebnis können wir ersehen, dass das 95 %-Konfidenzintervall für die Differenz zwischen den Grundgesamtheitsmittelwerten [-4,6895 Zoll, -1,1305 Zoll] beträgt.

Dies zeigt uns, dass wir zu 95 % sicher sein können, dass der tatsächliche Unterschied zwischen der durchschnittlichen Pflanzenhöhe von Art A und Art B zwischen -4,6895 Zoll und -1,1305 Zoll liegt.

Da 0 nicht in diesem Konfidenzintervall liegt , weist dies darauf hin, dass zwischen den Mittelwerten der beiden Grundgesamtheiten ein statistisch signifikanter Unterschied besteht.

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in SAS ausführen:

So führen Sie einen T-Test bei einer Stichprobe in SAS durch
So führen Sie einen T-Test bei zwei Stichproben in SAS durch
So führen Sie einen T-Test für gepaarte Stichproben in SAS durch