So verwenden sie die proc glmselect-anweisung in sas

Sie können die PROC GLMSELECT- Anweisung in SAS verwenden, um das beste Regressionsmodell basierend auf einer Liste potenzieller Prädiktorvariablen auszuwählen.

Das folgende Beispiel zeigt, wie diese Anweisung in der Praxis verwendet wird.

Beispiel: Verwendung von PROC GLMSELECT in SAS zur Modellauswahl

Angenommen, wir möchten ein multiples lineares Regressionsmodell anpassen, das (1) die Anzahl der Lernstunden, (2) die Anzahl der abgelegten Vorbereitungsprüfungen und (3) das Geschlecht verwendet, um die Abschlussnote der Prüfung der Schüler vorherzusagen.

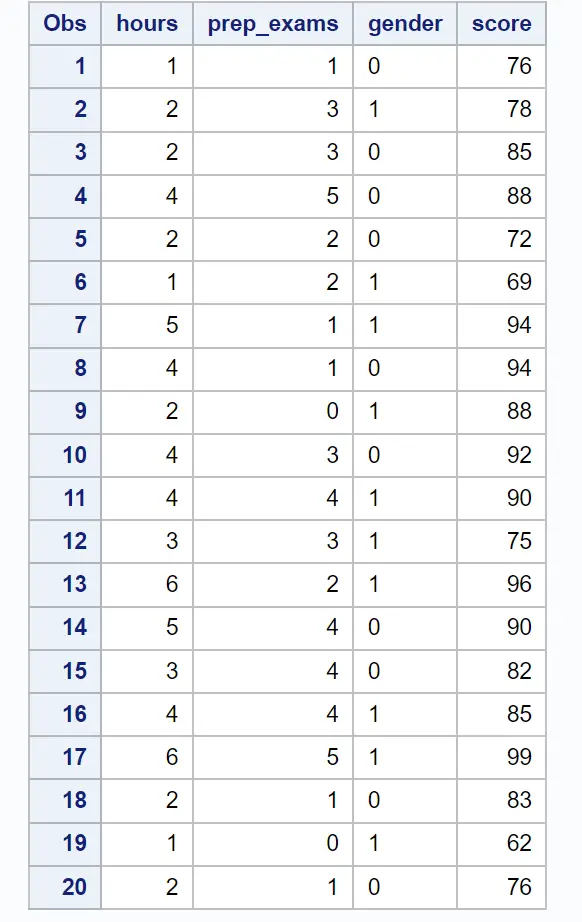
Zuerst verwenden wir den folgenden Code, um einen Datensatz mit diesen Informationen für 20 Schüler zu erstellen:

 /*create dataset*/
data exam_data;
    input hours prep_exams gender $score;
    datalines ;
1 1 0 76
2 3 1 78
2 3 0 85
4 5 0 88
2 2 0 72
1 2 1 69
5 1 1 94
4 1 0 94
2 0 1 88
4 3 0 92
4 4 1 90
3 3 1 75
6 2 1 96
5 4 0 90
3 4 0 82
4 4 1 85
6 5 1 99
2 1 0 83
1 0 1 62
2 1 0 76
;
run ;

/*view dataset*/
proc print data =exam_data;

Als Nächstes verwenden wir die PROC GLMSELECT -Anweisung, um die Teilmenge der Prädiktorvariablen zu identifizieren, die das beste Regressionsmodell erzeugt:

 /*perform model selection*/
proc glmselect data =exam_data;
    classgender ;
    model score = hours prep_exams gender;
run ;

Hinweis : Wir haben das Geschlecht in die Klassenanweisung aufgenommen, da es sich um eine kategoriale Variable handelt.

Die erste Tabellengruppe in der Ausgabe zeigt einen Überblick über die GLMSELECT-Prozedur:

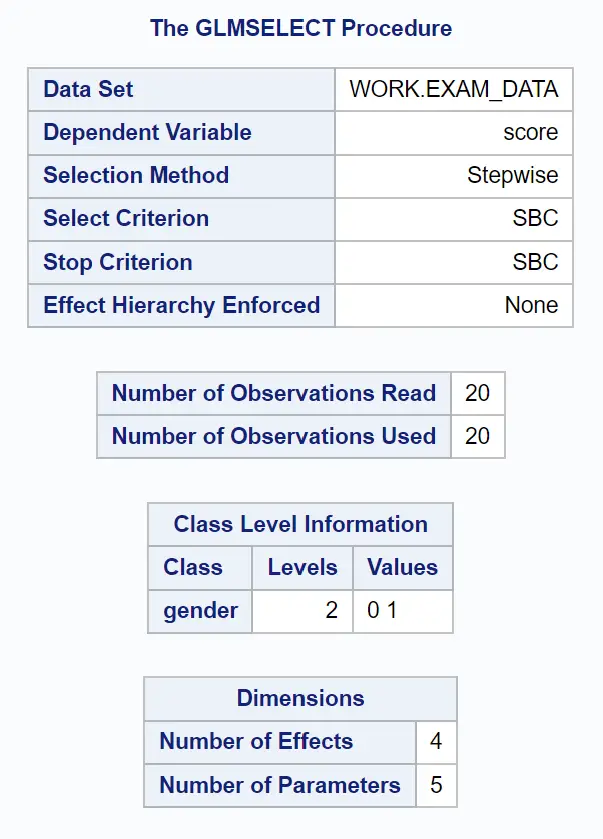
Wir können sehen, dass das Kriterium, das zum Stoppen des Hinzufügens oder Entfernens von Variablen aus dem Modell verwendet wurde, SBC war, das Schwarz-Informationskriterium , manchmal auch Bayes’sches Informationskriterium genannt.

Im Wesentlichen fügt die PROC GLMSELECT- Anweisung dem Modell so lange Variablen hinzu oder entfernt sie, bis sie das Modell mit dem niedrigsten SBC-Wert findet, das als „bestes“ Modell gilt.

Die folgende Tabellengruppe zeigt, wie die schrittweise Auswahl endete:

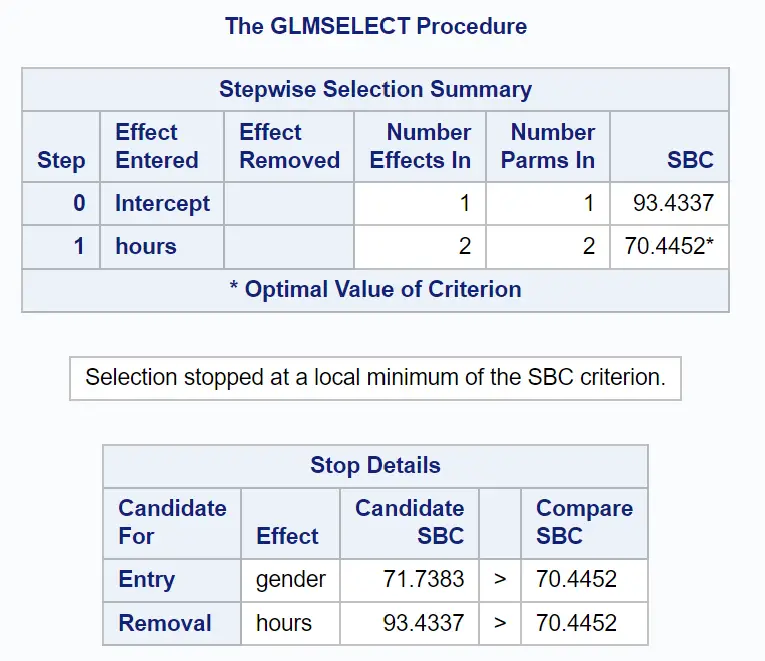
Wir können sehen, dass ein Modell, das nur den ursprünglichen Term enthielt, einen SBC-Wert von 93,4337 hatte.

Durch das Hinzufügen von Stunden als Prädiktorvariable im Modell sank der SBC-Wert auf 70,4452 .

Der beste Weg, das Modell zu verbessern, bestand darin, das Geschlecht als Prädiktorvariable hinzuzufügen, aber dadurch erhöhte sich der SBC-Wert tatsächlich auf 71,7383.

Somit umfasst das endgültige Modell nur den Intercept-Term und die untersuchten Zeiten.

Der letzte Teil des Ergebnisses zeigt die Zusammenfassung dieses angepassten Regressionsmodells:

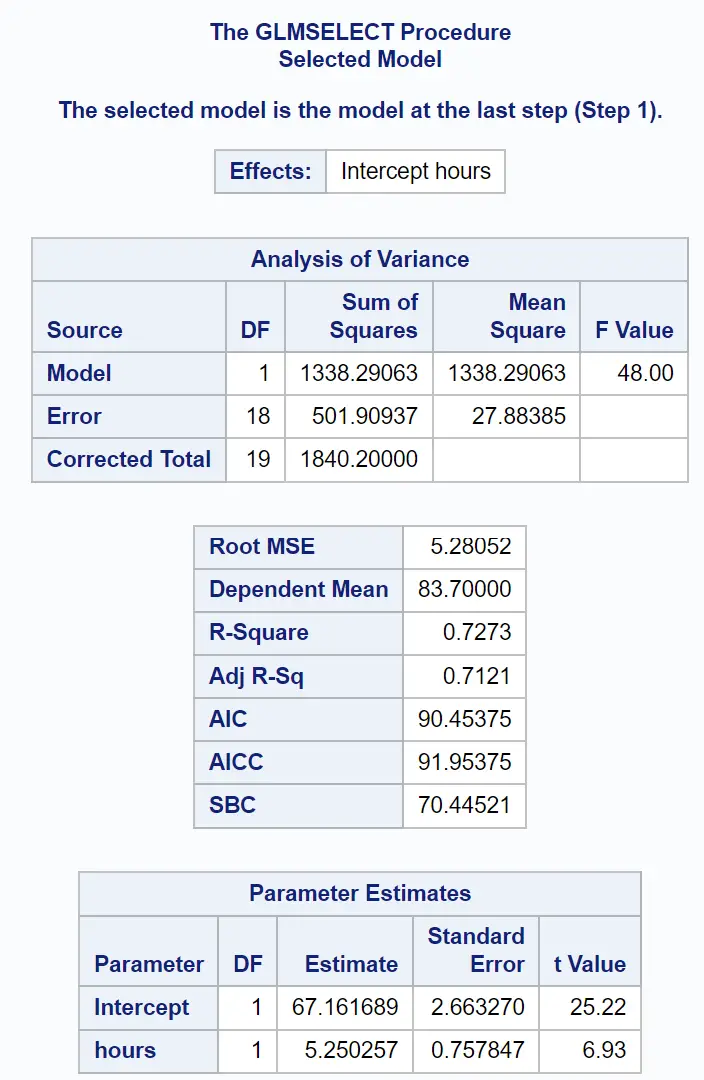
Wir können die Werte in der Tabelle „Parameterschätzungen“ verwenden, um das angepasste Regressionsmodell zu schreiben:

Prüfungsergebnis = 67,161689 + 5,250257 (Studienstunden)

Wir können auch verschiedene Metriken sehen, die uns sagen, wie gut dieses Modell zu den Daten passt:

Der R-Quadrat- Wert gibt uns den Prozentsatz der Variation in den Prüfungsergebnissen an, der durch die Anzahl der Lernstunden und die Anzahl der abgelegten Vorbereitungsprüfungen erklärt werden kann.

In diesem Fall lassen sich 72,73 % der Abweichungen in den Prüfungsergebnissen durch die Anzahl der Lernstunden und die Anzahl der abgelegten Vorbereitungsprüfungen erklären.

Es ist auch hilfreich, den Root-MSE- Wert zu kennen. Dies stellt den durchschnittlichen Abstand zwischen den beobachteten Werten und der Regressionsgeraden dar.

In diesem Regressionsmodell weichen die beobachteten Werte im Durchschnitt um 5,28052 Einheiten von der Regressionsgeraden ab.

Hinweis : Eine vollständige Liste potenzieller Argumente, die Sie mit PROC GLMSELECT verwenden können, finden Sie in der SAS-Dokumentation .

Zusätzliche Ressourcen

In den folgenden Tutorials wird erläutert, wie Sie andere häufige Aufgaben in SAS ausführen:

So führen Sie eine einfache lineare Regression in SAS durch
So führen Sie eine multiple lineare Regression in SAS durch
So führen Sie eine Polynomregression in SAS durch
So führen Sie eine logistische Regression in SAS durch