Satz von bayes

Von August 1, 2023 Wahrscheinlichkeit Keine Kommentare

In diesem Artikel wird erklärt, was der Satz von Bayes ist und wofür er in der Wahrscheinlichkeitsrechnung und Statistik verwendet wird. So erfahren Sie, wie die Formel des Bayes-Theorems lautet, gelöste Beispiele des Bayes-Theorems und welche Anwendungsmöglichkeiten dieses Theorems gibt.

Was ist der Satz von Bayes?

In der Wahrscheinlichkeitstheorie ist der Satz von Bayes ein Gesetz zur Berechnung der Wahrscheinlichkeit eines Ereignisses, wenn a priori Informationen über dieses Ereignis bekannt sind.

Genauer gesagt setzt der Satz von Bayes die Wahrscheinlichkeit von Ereignis A bei gegebenem Ereignis B mathematisch mit der Wahrscheinlichkeit von B bei gegebenem Ereignis A in Beziehung.

Wenn Sie beispielsweise im Voraus wissen, wie wahrscheinlich es ist, dass eine Person Kopfschmerzen hat, wenn sie an einer Grippe leidet, können Sie mithilfe des Bayes-Theorems die Wahrscheinlichkeit ermitteln, mit der eine Person an Grippe erkrankt, wenn sie Kopfschmerzen hat.

Der Satz von Bayes hat viele Anwendungsmöglichkeiten, beispielsweise wird er in der Medizin, Wirtschaft oder Technik verwendet, um die Wahrscheinlichkeiten bestimmter Ereignisse zu berechnen, die durch andere Ereignisse bedingt sind. Im Folgenden gehen wir detailliert auf die verschiedenen Anwendungen des Satzes von Bayes ein.

Der Satz von Bayes wurde vom englischen Mathematiker Thomas Bayes (1702-1761) erfunden, obwohl er 1763 posthum veröffentlicht wurde.

Formel des Satzes von Bayes

Der Satz von Bayes besagt, dass wir bei einem Beispielraum, der aus einer Menge sich gegenseitig ausschließender Ereignisse {A 1 , A 2 ,…, A i ,…, A n } besteht, deren Wahrscheinlichkeiten nicht Null sind, und einem anderen Ereignis B die Bedingung mathematisch in Beziehung setzen können Wahrscheinlichkeit von A i bei gegebenem Ereignis B mit der bedingten Wahrscheinlichkeit von B bei gegebenem A i .

Die Formel für den Satz von Bayes , auch Bayes-Regel genannt, lautet also:

Formel des Bayes-Theorems, Bayes-Regel

Gold:

  • P(A_i|B)

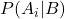
    ist die bedingte Wahrscheinlichkeit des Ereignisses A bei gegebenem Ereignis B, die sogenannte hintere Wahrscheinlichkeit.

  • P(B|A_i)

    ist die bedingte Wahrscheinlichkeit des Ereignisses B bei gegebenem Ereignis A i .

  • P(A_i)

    ist die Wahrscheinlichkeit, dass das Ereignis A i eintritt, die sogenannte A-priori-Wahrscheinlichkeit.

Beachten Sie, dass der Nenner der Formel des Bayes-Theorems die Gesamtwahrscheinlichkeit des Ereignisses B ist.

Beispiel für den Satz von Bayes

Sobald wir die Definition des Bayes-Theorems und seine Formel gesehen haben, sehen wir ein gelöstes Beispiel dafür, wie eine Wahrscheinlichkeit mit dem Bayes-Theorem berechnet wird, um das Konzept besser zu verstehen.

  • Ein Elektronikgeschäft verkauft drei Fernsehmarken: Wie hoch ist bei einem defekten Fernseher die Wahrscheinlichkeit, dass es sich um einen Fernseher der Marke Z handelt?

Die Übung gibt uns die Wahrscheinlichkeiten an, mit denen ein Kunde jede Fernsehmarke kaufen wird:

  • Ereignis A 1 : Ein Kunde kauft einen Fernseher der Marke X → P(A 1 )=0,20
  • Ereignis A 2 : Ein Kunde kauft einen Fernseher der Marke Y → P(A 2 )=0,50
  • Ereignis A 3 : Ein Kunde kauft einen Fernseher der Marke Z → P(A 3 )=0,30

Darüber hinaus gibt uns der Messwert auch die Wahrscheinlichkeit, dass ein Fernseher jeder Marke defekt ist:

Ereignis B: Der Fernseher ist defekt

  • B|A 1 : Bei einem Fernseher der Marke X ist der Fernseher defekt → P(B|A 1 )=0,05
  • B|A 2 : Bei einem Fernseher der Marke Y ist der Fernseher defekt → P(B|A 2 )=0,03
  • B|A 3 : Bei einem Fernseher der Marke Z ist der Fernseher defekt → P(B|A 3 )=0,04

Der Wahrscheinlichkeitsbaum aller Ereignisse, die uns interessieren, sieht also wie folgt aus:

Baumdiagramm des Bayes-Theorems

Um also die Wahrscheinlichkeit zu berechnen, dass es sich bei einem defekten Fernseher um die Marke Z handelt, müssen wir die Formel aus dem Satz von Bayes verwenden:

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

Unter Verwendung der in diesem Beispiel verwendeten Terminologie sieht die Formel von Bayes wie folgt aus:

P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}

Die Berechnung der Wahrscheinlichkeit, dass es sich bei einem bestimmten defekten Fernseher um die Marke Z handelt, lautet also wie folgt:

\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,04\cdot 0,30}{0,05\cdot 0,20+0,03\cdot 0,50+0,04\cdot 0,30}\\[2ex]&=0,32\end{aligned}

Zusammenfassend lässt sich sagen, dass die Wahrscheinlichkeit, dass es sich bei einem defekten Fernseher um die Marke Z handelt, bei 32 % liegt.

Anwendungen des Satzes von Bayes

Es gibt viele Anwendungen des Satzes von Bayes, darunter:

  1. Medizinische Tests : Das Bayes-Theorem wird in der Medizin häufig verwendet, um die Wahrscheinlichkeit zu bestimmen, diagnostische Tests zu bestehen. Beispielsweise kann bei einem HIV-Test mit dem Theorem die Wahrscheinlichkeit berechnet werden, dass eine Person tatsächlich mit dem Virus infiziert ist, wenn das Testergebnis positiv ausfällt.
  2. Finanzanalyse : Im Finanzwesen wird das Bayes-Theorem verwendet, um die Wahrscheinlichkeit zu berechnen, dass bestimmte wirtschaftliche Ereignisse, wie z. B. ein Anstieg oder Rückgang des Aktienwerts, bei einer Reihe wirtschaftlicher Variablen eintreten.
  3. Marktforschung : Mit dem Bayes-Theorem lässt sich beispielsweise die Wahrscheinlichkeit ermitteln, mit der eine Person ein Produkt kauft, nachdem sie eine Werbung für dieses Produkt gesehen hat.
  4. Wettervorhersage : Wettermodelle verwenden auch den Satz von Bayes, um die Wahrscheinlichkeit zu bestimmen, dass eine bestimmte Wettervorhersage auf der Grundlage beobachteter Daten wahr wird. Dies verbessert die Genauigkeit von Klimavorhersagen.
  5. Computersicherheit – In der Cybersicherheit kann das Bayes-Theorem angewendet werden, um die Wahrscheinlichkeit zu bestimmen, dass eine verdächtige Aktivität tatsächlich ein Angriff auf das Computersystem ist.

Probleme mit dem Bayes-Theorem gelöst

Übung 1

Es wird geschätzt, dass 1 % der Bevölkerung an einer Krankheit leidet. Ein Test zum Nachweis dieser Krankheit ist bei positiven Fällen zu 95 % und bei negativen Fällen zu 90 % genau. Wenn eine zufällig ausgewählte Person positiv getestet wird, wie hoch ist dann die Wahrscheinlichkeit, dass sie tatsächlich an der Krankheit leidet?

Die Übungsanweisung gibt uns die folgenden Wahrscheinlichkeiten:

A 1 : Die Person hat die Krankheit → P(A 1 )=0,01
A 2 : Die Person hat die Krankheit nicht → P(A 2 )=0,99

B: Der Test ist positiv
B|A 1 : Der Test ist positiv, wenn die Person an der Krankheit leidet → P(B|A 1 )=0,95
B|A 2 : Der Test ist positiv, wenn die Person nicht an der Krankheit leidet → P(B|A 2 )=1-0,90=0,10

Um dann die Wahrscheinlichkeit zu berechnen, dass eine zufällig ausgewählte Person bei positivem Test tatsächlich an der Krankheit leidet, muss die Bayes-Regel angewendet werden:

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

P(A_1|B)=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}

Also setzen wir die Werte in die Formel ein und führen die Wahrscheinlichkeitsberechnung durch:

\begin{aligned}P(A_1|B)&=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}\\[2ex]&=\cfrac{0,95\cdot 0,01}{0,95\cdot 0,01+0,10\cdot 0,99}\\[2ex]&=0,0876\end{aligned}

Kurz gesagt beträgt die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person positiv getestet wird und tatsächlich an der Krankheit leidet, 8,76 %.

Übung 2

Es wird geschätzt, dass die Wahrscheinlichkeit, dass eine Aktie an einem Tag steigt, bei 40 % liegt, dass sie stabil bleibt bei 10 % und dass sie fällt bei 50 %. Darüber hinaus wissen wir, dass bei einem Marktanstieg die Wahrscheinlichkeit, dass ein Finanzanalyst die richtige Vorhersage trifft, bei 90 % liegt, dass bei stabilem Markt die Wahrscheinlichkeit, dass die Vorhersage richtig ist, bei 75 % liegt und dass bei einem Rückgang die Wahrscheinlichkeit, dass der Markt richtig ist, bei 75 % liegt. die Wahrscheinlichkeit einer korrekten Vorhersage beträgt 75 %. 85%.%. Wenn ein Analyst vorhersagt, dass der Markt fallen wird, wie wahrscheinlich ist es dann, dass er tatsächlich fallen wird?

In diesem Fall liefert uns die Übungsaussage die folgenden Wahrscheinlichkeiten:

A 1 : Der Markt steigt an einem Tag → P(A 1 )=0,40
A 2 : Der Markt bleibt über einen Tag stabil → P(A 2 )=0,10
A 3 : Der Markt steigt an einem Tag → P(A 3 )=0,50

B: Der Analyst prognostiziert, dass der Markt fallen wird
B|A 1 : Der Analyst sagt richtig voraus, dass der Markt wachsen wird → P(B|A 1 )=0,90
B|A 2 : Der Analyst sagt richtig voraus, dass der Markt stabil bleibt → P(B|A 2 )=0,75
B|A 3 : Der Analyst sagt richtig voraus, dass der Markt fallen wird → P(B|A 3 )=0,85

Um die Wahrscheinlichkeit zu bestimmen, mit der ein Analyst eine Vorhersage trifft, dass der Markt fallen wird und diese richtig ist, müssen wir die Formel des Bayes-Theorems verwenden:

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}

Wir setzen die Wahrscheinlichkeitswerte in die Bayes-Formel ein und berechnen die Wahrscheinlichkeit:

\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,85\cdot 0,50}{0,90\cdot 0,40+0,75\cdot 0,10+0,85\cdot 0,50}\\[2ex]&=0,4942\end{aligned}

Daher liegt die Wahrscheinlichkeit, dass ein Analyst Recht hat, wenn er sagt, dass der Aktienmarkt fallen wird, bei 49,42 %.

Über den Autor

Benjamin Anderson
Dr. Benjamin Anderson

Hallo, ich bin Benjamin, ein pensionierter Statistikprofessor, der sich zum engagierten Statorials-Lehrer entwickelt hat. Mit umfassender Erfahrung und Fachwissen auf dem Gebiet der Statistik bin ich bestrebt, mein Wissen zu teilen, um Studenten durch Statorials zu befähigen. Mehr wissen

Einen Kommentar hinzufügen

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert