Satz von tschebyschew

In diesem Artikel wird erklärt, was der Satz von Tschebyscheff ist. Hier finden Sie die Formel des Tschebyscheff-Theorems, eine gelöste Aufgabe und zusätzlich einen Online-Rechner des Tschebyscheff-Theorems. Schließlich wird der Unterschied zwischen dem Satz von Tschebyschew und der empirischen Regel aufgezeigt.

Was ist der Satz von Tschebyschew?

Der Satz von Tschebyscheff , auch bekannt als Tschebyscheff-Ungleichung , ist eine statistische Regel zur Berechnung der Wahrscheinlichkeit, dass ein Wert einer Zufallsvariablen in einem bestimmten Abstand von seinem Mittelwert liegt.

Mit anderen Worten: In der Statistik wird der Satz von Tschebyscheff verwendet, um die Wahrscheinlichkeit zu bestimmen, mit der ein Wert innerhalb eines Konfidenzintervalls liegt.

Darüber hinaus wird der Satz von Tschebyschew auch zum Beweis anderer statistischer Theoreme verwendet, beispielsweise des Gesetzes der großen Zahlen.

Obwohl der Satz von Tschebyschew erstmals vom Franzosen Irénée-Jules Bienaymé formuliert wurde, trägt der Satz seinen Namen, weil er 1867 vom Russen Pafnuty Tschebuschew erfunden wurde.

Formel des Satzes von Tschebyschew

Der Satz von Tschebyscheff besagt, dass die Wahrscheinlichkeit, dass ein Wert gleich k Standardabweichungen vom Mittelwert ist, größer oder gleich eins minus dem Verhältnis von eins dividiert durch k zum Quadrat ist.

Daher lautet die Formel für den Satz von Tschebyscheff wie folgt:

Gold

ist der Wert der Zufallsvariablen,

das arithmetische Mittel der Variablen,

seine Standardabweichung und

die Anzahl der Standardabweichungen vom Mittelwert, über die die Wahrscheinlichkeit berechnet werden soll.

Beachten Sie, dass diese Formel nur verwendet werden kann, wenn die Anzahl der Standardabweichungen, anhand derer die Berechnung durchgeführt wird, größer als 1 ist, d. h. wenn k größer als 1 ist.

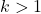Sie können den Online-Rechner des Chebyshev-Theorems unten verwenden, um die Wahrscheinlichkeit zu berechnen.

Beispiel für den Satz von Tschebyschew

Nachdem wir die Definition des Chebyshev-Theorems und seine Formel gesehen haben, finden Sie hier ein gelöstes Beispiel dieses statistischen Theorems, um das Konzept besser zu verstehen.

• Wenn die in der Kursstatistik einer Universität erzielten Noten durch eine Verteilung mit einem Mittelwert von 65 und einer Standardabweichung von 10 definiert werden, wie viel Prozent der Studierenden haben eine Note zwischen 50 und 80 erhalten?

Um dieses Problem zu lösen, müssen wir die Formel des Satzes von Tschebyscheff anwenden. Allerdings müssen wir zunächst ermitteln, wie viele Standardabweichungen die Werte 50 und 80 vom Mittelwert der Variablen haben. Dazu müssen wir lediglich die folgende Berechnung durchführen:

Daher entsprechen die Werte 50 und 80 1,5 Standardabweichungen vom unteren bzw. oberen Mittelwert. Wir verwenden daher die Formel des Chebysheva-Theorems mit k=1,5:

So erreichten immerhin 55,56 % der Studierenden eine Note zwischen 50 und 80.

Chebyshev-Theorem-Rechner

Geben Sie die Anzahl der Standardabweichungen zwischen den betreffenden Werten und dem Mittelwert (k) ein und klicken Sie dann auf „Berechnen“. Der Rechner gibt dann die minimale Wahrscheinlichkeit des Konfidenzintervalls zurück.

Sie müssen die Anzahl der Standardabweichungen mit dem Punkt als Dezimaltrennzeichen eingeben.

Satz und Faustregel von Tschebyschew

Zwei eng verwandte Konzepte in der Statistik sind der Satz von Tschebyschew und die empirische Regel, da beide zur Berechnung der Wahrscheinlichkeit von Konfidenzintervallen verwendet werden.

Der Unterschied zwischen dem Satz von Tschebyschew und der empirischen Regel besteht darin, dass der Satz von Tschebyschew auf jede Art von Verteilung angewendet werden kann, während die empirische Regel nur für eine Normalverteilung gilt.

Die Verwendung des Satzes von Tschebyscheff ist daher umfassender, die empirische Regel liefert jedoch genauere Ergebnisse für eine Normalverteilung.

Klicken Sie hier, um die genaue Faustregel zu sehen: